NEW SCIENCES FOR A NEW ERA:
Mathematical, Physical and Chemical Discoveries of
Ruggero Maria Santilli
I. Gandzha and J Kadeisvili
PRINTED VERSION
I. Gandzha and J Kadeisvili, New Sciences for a New Era:
Mathematical, Physical and Chemical Discoveries of
Ruggero Maria Santilli,
Sankata Printing Press, University of Kathmandy, Nepal (2011),
Free pdf download
http://www.santilli-foundation.org/docs/RMS.pdf
CHAPTER 6:
REDUCTION OF MATTER TO
PROTONS AND ELECTRONS
TABLE OF CONTENTS
6.1. INTRODUCTION
6.1A. Foreword
6.1B. Santilli's recollections on the birth of hadronic mechanics
6.1C. New structure model of unstable hadrons and leptons
6.1D. Inapplicability of quantum mechanics to the structure of hadrons
6.1E. The dichotomy: classification vs structure of hadrons and leptons
6.2. REDUCTION OF MESONS AND LEPTONS TO ELECTRONS AND POSITRONS
6.2A. Conception of the πo structure
6.2B. Structure equation of the πo
6.2C. Solution of the πo structure equation
6.2D. Structure model of unstable leptons and of the remaining mesons
6.2E. Revisions due to the isodual theory of antimatter
6.2F. Compatibility of the new structure model of hadrons with unitary classifications
6.2G. Experimental verifications
6.3. REDUCTION OF BARYONS TO PROTONS AND ELECTRONS
6.3A. Conception of the neutron structure
6.3B. Nonrelativistic exact representation of the neutron rest energy, meanlife and charge radius
6.3C. Nonrelativistic, exact and invariant representation of the neutron spin
6.3D. Nonrelativistic, exact and invariant representation of the neutron magnetic moment
6.3E. Foudations of the relativistic treatment
6.3F. Relativistic, exact and invariant representation of the neutron rest energy, meanlife and charge radius
6.3G. Relativistic, exact and invariant representation of the neutron spin
6.3H. Relativistic, exact representation of the anomalous magnetic moment of the neutron
6.3I. Santilli's etherino vs Fermi's neutrino
6.3J. Structure model of the remaining baryons with physical constituents
6.3K. Compatibility of baryon syntheses with the SU(3) classification
6.4. LABORATORY SYNTHESIS OF NEUTRONS FROM A HYDROGEN GAS
6.4A. Introduction
6.4B. Don Borghi experiment on the synthesis of neutrons from an hydrogen gas
6.4C. Santilli experiment on the synthesis of neutrons from a hydrogen gas
6.4D. The Don Borghi-Santilli neutroids
6.4E. Interpretation of Don Borghi and Santilli experiments
6.4F. Santilli's prediction of a new class of nuclides
6.4G. Requirements for the re-run of Santilli's experiments
6.5. REDUCTION OF NUCLEI TO PROTONS AND ELECTRONS
6.5A. Introduction
6.5B. Santilli's contributions in nuclear physics
6.5C. Review of basic nuclear contributions
6.5D. Review of Lie-isotopic nuclear contributions
6.5E. Review of Lie-admissible nuclear contributions
6.5F. Reduction of the deuterium to two protons and one electron
6.5Fa. Foreword
6.5Fb. Insufficiencies of quantum mechanics for the deuterium structure
6/5Fc. Conception of the deuteron structure
6.5Fd. Representation of the stability of the deuterium
6.5Fe. Representation of the deuterium size
6.5Ff. Representation of the deuterium charge
6.5Fg. Representation oof the deuterium spin
6.5Fh. Representation of the deuterium magnetic moment
6.5Fi. Representation of the deuterium force
6.5Fj. Representation of the deuterium total energy
6.5Fk. Representation of the deuterium electric dipole moment and parity
6.6. REDUCTION OF MATTER TO PROTONS AND ELECTRONS
6.7. REDUCTION OF NEUTRON STARS TO PROTONS AND ELECTRONS
6.1. INTRODUCTION
6.1A. Foreword
Hadronic mechanics has been conceived, built and verified to achieve one of the biggest syntheses in scientific history: the reduction of matter to protons and electrons. Santilli's view is that stars initiate their lives as being solely composed of hydrogen; they first synthesize neutrons from protons and electrons; and then they synthesize all elements existing in nature. Therefore, a consistent interpretation of the neutron as a bound state of a proton and an electron under a generalized mechanics ensures the achievement of the indicated reduction.
The first major difficulty facing said reduction, whose solution required decades of research, is that quantum mechanics prohibits the neutron from being a bound state of a proton and an electron for numerous reasons studied in this chapter, such as the impossibility of representing the spin, rest energy, magnetic moment, charge radius, and other features of the neutron.
Santilli has shown that quantum mechanics is exactly valid for the dynamics of the proton and the electron when at the large mutual distance of the hydrogen atom, in which case only potential and, therefore, Hamiltonian interactions occur with their well known unitary time evolution. By contrast, Santilli has shown that quantum mechanics is inapplicable (rather than being "violated") for the conditions of total mutual penetration of the electron within the hyperdense medium inside the proton.
In fact, the latter conditions imply the emergence of fundamentally new interactions of contact, nonpotential and non-Hamiltonian type that, as such, require a generalized mechanics with a nonunitary time evolution (evidently in view of its non-Hamiltonian character). This is a main motivation for the proposal, construction and verification of hadronic mechanics as a nonunitary covering of quantum mechanics.
Another major difficulty in the achievement of the indicated reduction is the rather general belief that the neutron is a bound state of particles, known as quarks, that cannot be directly detected, yet are popularly believed as being real particles in our spacetime, thus obstructing alternative views. However, as Santilli puts it:
It has been impossible for me to believe that, at the time of the synthesis of the neutron inside a star, the permanently stable proton and electron simply "disappear" from our universe to be replaced by the hypothetical quarks, and then, at the time of the neutron decay, the proton and the electron simply "reappear" by academic fiat. Rather than conjecturing the existence of hypothetical particles for the evident purpose of maintaining the validity of a preferred theory inside hadrons, I elected instead to adapt the theory to nature and represent the neutron as a generalized bound state of a proton and an electron which is quantitatively possible when admitting their condition of total mutual penetration, with resulting non-Hamiltonian, thus nonunitary time evolution.
In essence, Santilli fully accepts SU(3)-color theories, also called the "standard model," as providing the final Mendeleev-type classification of hadrons into families; he accepts quarks as being necessary for the elaboration of SU(3) theories; but he considers quarks what they technically are, purely mathematical representations of a unitary symmetry that cannot be even defined in our spacetime; and has established a basically novel structure models of hadrons with physical constituents in such a way to reach full compatibility with the SU(3) classification.
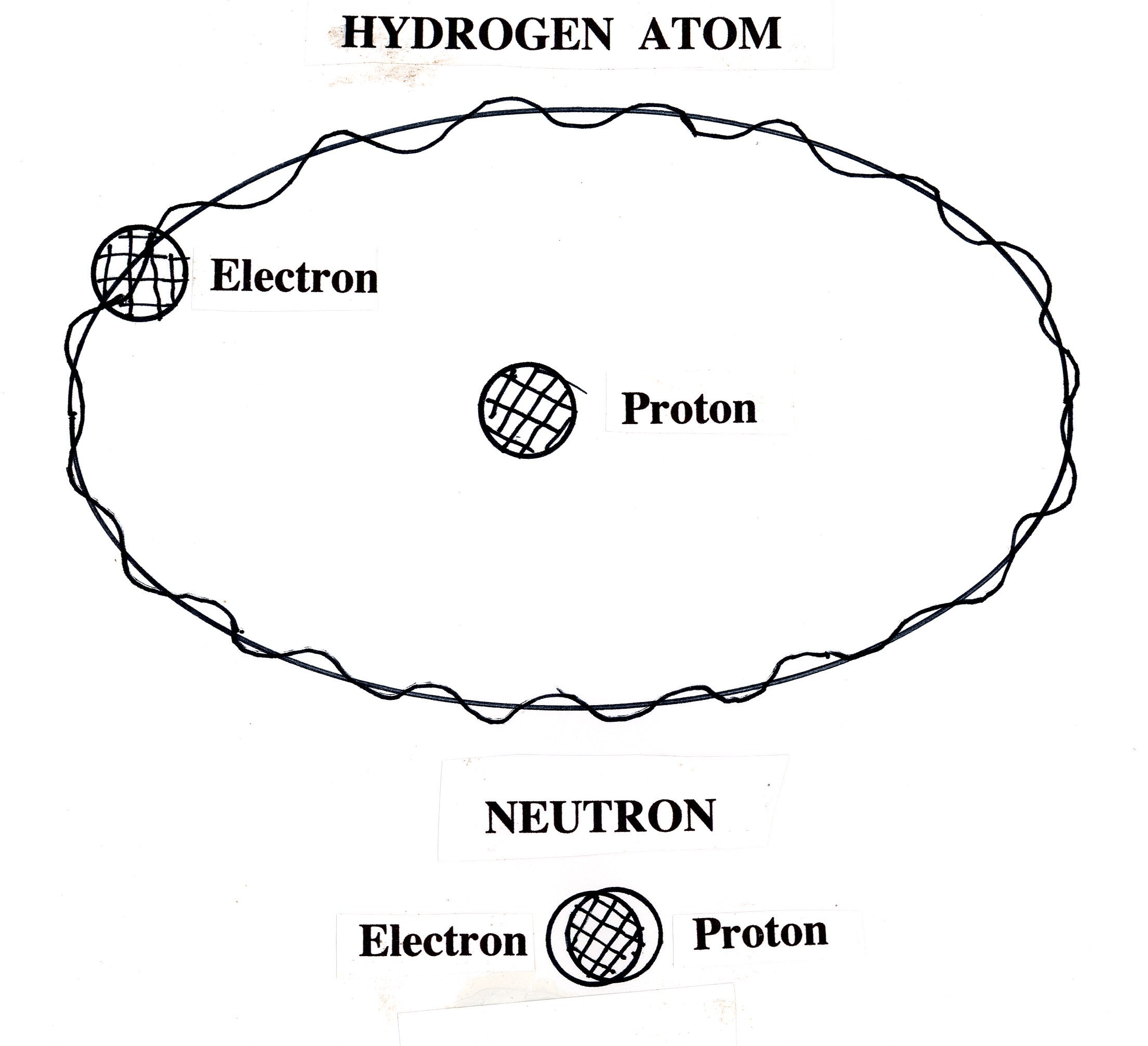
Figure 6.1: An original drawing used by Santilli in his lectures to illustrate the dramatic physical differences between the hydrogen atom and the neutron synthesis from a proton and an electron as occurring in stars. In the former case, the large mutual distance allows an effective point-like abstraction of the proton and the electron, resulting in the exact validity of quantum mechanics. In the latter case, the use of the same abstraction causes the exiting from the boundary of science in favor of theologies due to the condition of total penetration of the electron within the hyperdense medium inside the proton, with the resulting inapplicability of quantum mechanics due to the emergence of contact non-Hamiltonian forces that are basically absent in the hydrogen structure.
A main objective of this chapter is to review the scientific process that lead to the exact and invariant representation of all characteristics of the neutron as a generalized bound state of a proton and an electron in conditions of total mutual penetration that, as such, cause their lifting into generalized particles described by hadronic mechanics and its basic isosymmetries.
The structure of nuclei parallels that of the neutron. In fact, nuclei were originally conceived as bound states of protons and electrons because, as recalled above, all nuclei originate from hydrogen. Subsequently, it became known that such a nuclear conception is prohibited by quantum mechanics. The achievement of an exact representation of the neutron as a bound state of a proton and an electron under the laws of hadronic mechanics automatically assures the reduction of nuclei to protons and electrons.
Additionally, Santilli has shown that such a representation is necessary for the exact representation of numerous basic nuclear data left unresolved by quantum mechanics, such as the spin 1 of the deuteron, the stability of the neutron in certain but not all nuclei, the nuclear force, and other aspects. Needless to say, the current representation of nuclei as a quantum mechanical bound state of protons and neutrons does remain valid, but only as a first approximation of a much more complex physical reality.
Rather than being mere academic semantic, the reduction of nuclei to protons and electrons has rather serious social, let alone scientific, relevance because, as shown in the next chapter, it allows the conception and industrial development of basically new clean energies called hadronic energies, rather than nuclear energies, because originating from mechanisms in the structure of hadrons, rather than in their collection (as it is the case for known nuclear energies). As a matter of fact, this chapter is a pre-requisite for the new clean energies studies in the next chapter.
In this chapter we shall solely use the Lie-isotopic, time reversible branch of hadronic mechanics because the neutron synthesis is reversible over time, thus not requiring the broader, irreversible, Lie-admissible mechanics. For simplicity we shall use the ordinary associative multiplication AxB = AB of generic quantities A, B, and avoid the use of the multiplication symbol "x." This essentially means that the presentation of this chapter deals with the "projection" of the various models in our spacetime. The understanding is that the axiomatically correct formulation is solely that on isospaces over isofields and related isotopic product as presented in Chapter 2.
To prevent the "impression" of criticisms that in reality have no scientific ground, readers with a vast knowledge of quantum mechanics but insufficient knowledge of the covering hadronic mechanics are suggested to acquire a minimal technical knowledge of the preceding presentations prior to venturing judgments on the content of this chapter.
6.1B. Santilli's recollections on the birth of hadronic mechanics
Hadronic mechanics was technically born with my 1967-1968 papers on the Lie-admissible and Jordan admissible mutation (deformation) of Lie algebras and, consequently, of Heisenberg's equation, that were part of my Ph. D. studies at the University of Torino, Italy,
Embedding of Lie-algebras in non associative structures
R. M. Santilli, Nuovo Cimento Vol. 51, 570-576 (1967).
and other papers of that period. such as
An introduction to Lie-admissible algebras
R. M. Santilli,
Supplemento al Nuovo Cimento Vol. 6, pages 1225-1249 (1968)
Dissipativity and Lie-admissible algebras
R. M. Santilli,
Meccanica, Vol. 1, pages 3-11 (1969)
In August of 1967 I moved with my family to the USA where I soon realized that it would have been impossible for me to locate an academic job based on Lie-admissible and Jordan-admissible research since these algebras were unknown at that time in the U. S. mathematics, let alone physics. Hence, I dedicated myself to more mundane research that can be identified in my curriculum, even though i continued the study of Lie-admissible and Jordan-admissible covering theories.
When I joined the Lyman Laboratory of Physics at Harvard University in September 7, 1977, during the very day of my arrival, I was invited by ERDA, soon to become the the DOE, to apply for the grant number ER-78-S-02-47420.A000. During my conversations with Dr. David Peaslee, the ERDA-DOE officer in charge of my grant, I was told the DOE preference, originated from the final days of Carter's Administration, to conduct "innovative studies on new clean energies and fuels."
Therefore, I plunged myself in the study of what I consider the biggest reservoir of clean energy available to mankind, the neutron. In fact, the neutron is naturally unstable and decays into a proton, a highly energetic electron whose energy can be easily captured with a metal shield and the innocuous neutrino (if it exists).
Along these lines, it became mandatory to initiate the study with the synthesis of the neutron as it occurs in stars, that is, as a "compressed hydrogen atom" according to Rutherford's original conception of 1920.
However, I immediately stumbled into a major technical problem. Schroedinger's equation is consistent for well known quantum mechanical bound states, those with a negative binding energy, as it is established for nuclear, atomic and molecular bound states. By comparison, the synthesis of the neutron requires 0.782 MeV energy (in which case there is no energy left for the hypothetical neutrino....).
I remember trying the impossible, day and night, to solve the Schroedinger equation with a "positive binding energy" to have completely inconsistent and, in any case, physically meaningless equations.
Eventually, I had to accept the inapplicability of quantum mechanics for the synthesis of the neutron from a proton and an electron as occurring in stars. I also discovered that the problem was rather general, inasmuch as quantum mechanics was inapplicable for the synthesis of all hadrons from massive particles produced in their spontaneous decays with lowest mode, inapplicability that signaled the lack of acceptance of important alternatives in particle physics of the 20th century, such as the so-called "boot-strap model."
At that point, I initiated the search for alternatives mechanics with the predictable outcome that physically consistent solutions for a "positive binding energy" are only possible under a "nonunitary image" of Schroedinger's equation. That signaled the conception, as well as the name of "hadronic mechanics" as currently known.
Before joining the Lyman Laboratory of Physics at Harvard University, I had been a member of the Department of Physics at MIT during which stay I had the opportunity of several pleasant scientific contacts with its chairman of the time, Herman Feshback, one of the world leaders of Schroedinger's equation with particular reference to its application in nuclear physics.
In early 1978, I called Herman asking for a meeting he kindly granted. On arrival at his office at MIT, I told Herman my inability to solve the Schroedinger equation for the neutron synthesis by saying "Herman, am I gone banana, or there is a real structural problem in this case?" Herman confirmed his deep knowledge of the field by immediately saying "Ruggero, the indicial equation of Schroedinger's equation has no physical solution for a bound state in which the total energy is bigger than the sum of the rest energies of the constituents."
In this way, I did have a confirmation that I was not gone banana and that the synthesis of the neutron was indeed a fundamental open problem of 20th century physics because beyond the class of unitary equivalence of quantum mechanics. Therefore, I said "Herman, your statement is indeed correct and remains valid under the most general possible unitary class of equivalence of quantum mechanics. However, you may be interested in knowing that I have apparently found physically consistent solutions via a nonunitary image of Schroedinger's equation."
At the hearing of that statement, Herman Feshback behavior changed dramatically; he left his desk; called me "Dr. Santilli;" and gave me the clear hint that the meeting was over. Therefore, I quickly left after saying thanks. I clearly understood that, at that point, I lost an academic friend due to his evident attachment to quantum mechanics, but I had gained something much more important, the awareness of the far reaching importance of the synthesis of the neutron.
Since that meeting, Herman Feshback became one of my worst academic enemies in the Cantabridgean area, as I reported and documented in
Ethical Probe of Einstein's Followers in the USA: An Insider's View
R. M. Santilli, Alpha Publishing (1984)
However, I want to express here my appreciation to Herman Feshback because of his crucial role in one of the most important scientific consultations of my life.
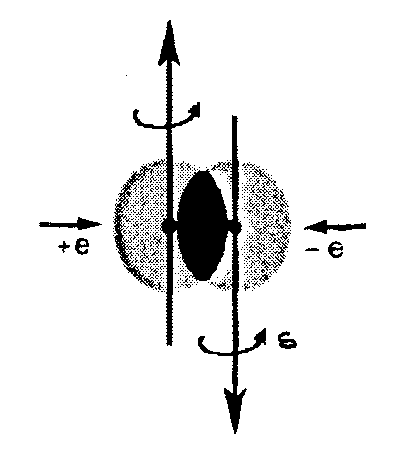
Figure 6.2: A schematic view of the main interactions absent in the structure of the hydrogen atom, but present in the neutron synthesis of Figure 6.1, the nonlinear, nonlocal and nonpotential interactions due to deep wave overlapping of extended particles. Their non-Hamiltonian character mandates a nonunitary covering of quantum mechanics. This motivated the birth of hadronic mechanics in Spring 1978.
On my way back to Harvard, I plunged myself full speed into the study of the most general possible nonunitary image of quantum mechanics. By using nonunitarity transforms of the 1967-1968 Lie-admissible and Jordan admissible equations, it was easy to reach the most general possible lifting of Schrodinger and Heisenberg equations for open irreversible and non-Hamiltonian processes.
Due to the primary application of the covering theory to the synthesis of the neutron and of other hadrons, I suggested the name of hadronic mechanics for the class of invariant nonunitary images of quantum mechanics, and proposed its construction in the two memoirs of 1978 under the indicated ERDA-DOE contract.
On a possible Lie-admissible covering of Galilei's relativity in Newtonian mechanics for nonconservative and Galilei form-noninvariant systems
R. M. Santilli, Hadronic J. Vol. 1, 223-423 (1978)
Need of subjecting to an experimental verification the validity within a hadron of Einstein special relativity and Pauli exclusion principle
R. M. Santilli, Hadronic J. Vol. 1, 574-901 (1978)
In Section 5 of the second memoir I solved completely the nonunitary image of Schroedinger's equation for the synthesis of the πo meson from the positronium. However, I could not even initiate the solution of the synthesis of the neutron due to numerous technical problems yet to be solved, including the isotopies of the SU(2)-spin symmetry, the achievement of invariance of numerical predictions over time, and other problems.
Preliminary maturity for the synthesis of the neutron was first reached at the nonrelativistic level in the 1990 paper
Apparent consistency of Rutherford's hypothesis on the
neutron as a compressed hydrogen atom
R. M. Santilli,
Hadronic J. Vol. 13, 513-531 (1990)
Apparent consistency of Rutherford's hypothesis on the neutron structure via the hadronic generalization of quantum mechanics - I: Nonrelativistic treatment
R. M. Santilli,
ICTP preprint # IC/91/47 (1992)
published in "Santilli's 1991 Papers at the ICTP", International Academic Press (1992)
and at the relativistic level in the JINR memoir
Recent theoretical and experimental evidence on the apparent
synthesis of neutrons from protons and electrons
R. M. Santilli, Communication of the JINR, Dubna, Russia, number JINR-E4-93-352 (1993) published in the
Chinese J. System Engineering and Electronics Vol. 6, 177-199 (1995)
Nevertheless, these studies still lacked invariance over time that was finally achieved in the 1997 memoirs for reversible and irreversible processes, respectively,
Relativistic hadronic mechanics: nonunitary, axiom-preserving
completion of relativistic quantum mechanics
R. M. Santilli,
Found. Phys. Vol. 27, 625-729 (1997)
Invariant Lie-admissible formulation of quantum deformations
R. M. Santilli,
Found. Phys. Vol. 27, 1159- 1177 (1997)
I outlined this laborious scientific journey in my monographs
Hadronic Mathematics, Mechanics and Chemistry, Volumes I, II, III, IV and V
R. M. Santilli, International Academic Press (2008)
Among various independent studies, a nice review dedicated to the neutron is that by Jerdsay Kadeisvili in the memoir
The Rutherford-Santilli neutron
J. V. Kadeisvili,
Hadronic J. Vol. 31, 1-114 (2008)
6.1C. New structure model of unstable hadrons and leptons
In the two memoirs, hereon referred to as 1978A and 1978B,
On a possible Lie-admissible covering of Galilei's relativity in Newtonian mechanics for nonconservative and Galilei form-noninvariant systems
R. M. Santilli, Hadronic J. Vol. 1, 223-423 (1978)
Need of subjecting to an experimental verification the validity within a hadron of Einstein special relativity and Pauli exclusion principle
R. M. Santilli, Hadronic J. Vol. 1, 574-901 (1978)
Santilli proposed a new structure model of unstable hadrons and leptons based on the following:
ASSUMPTION 1: Conventional quantum mechanics is exactly valid in the exterior problem of hadrons in vacuum resulting in a linear, local-differential and potential-Hamiltonian characterization of particles solely as being point-like;
ASSUMPTION 2: The size of wave packets and/or charge distributions of all particles is of about 1 fm. This establishes that hadronic constituents are in conditions of total mutual penetration, with consequential emergence of nonlinear, nonlocal-integral and nonpotential/non-Hamiltonian forces and the validity of the covering hadronic mechanics for interior structural problems;
ASSUMPTION 3: The constituents of unstable hadrons and leptons are conventional massive particles that can be produced free in the spontaneous decays;
ASSUMPTION 4: When immersed within a hadronic medium, constituents experience an alteration (called mutation) of all intrinsic characteristics as characterized by the the Lorentz-Poincare'-Santilli isosymmetry, and recover conventional characteristics when released free in vacuum;
ASSUMPTION 5: the number of elementary massive physical constituents of unstable hadrons and leptons increases with the increase of the mass as it is the case for nuclei, atoms and molecules.
In this chapter, we shall outline the new structure models by following its original derivation. To begin, in Section 5 of 1978B, Santilli initiated his new structure model with the lightest meson, the πo, by recalling that it decays spontaneously into an electron and a positron
Hence, Santilli assumed that the πo is a bound state of one mutated electron (isoelectron) e*- and one mutated positron (isopositron) e*+ (called in the original work eleton and antieleton) according to hadronic mechanics (hm),
by showing that it provides an exact representation of all characteristics of the particle considered, such as rest energy, meanlife, charge radius, charge, electric and magnetic moments and parity, including the primary decay
that is an evident confirmation of the assumed structure. Other decays (such as e-e+e-e+, e-e+γ, etc.) are caused by secondary processes, thus requiring hadronic field theory that is not studied in this chapter.
In the same memoir 1978B, Santilli noted that the π± meson admits the decay
Therefore, he assumed that the π± is a bound state of the mutated meson (isomeson) π*o and the isoelectron e*±, namely, it has three conventional, massive, elementary constituents with
along Assumption 5 on the increase of the number of massive physical constituents with mass (or energy), while keeping the approximate charge radius of 1 fm.
In order to prevent the impression of having valid criticisms, the reader should be aware that the spin zero of the π± is represented exactly by the isosymmetries of hadronic mechanics, while being impossible for quantum mechanics. Hence, the study of the Lie-Santilli isotheory is suggested prior to venturing comments, due to the novelty of the field.
Note also that hadronic mechanics permits the reduction of a three-body to a two-body structure, thus allowing a full exact analytic solution similar to that achieved later on by Santilli and Shillady on the hydrogen structure (Chapter 4). Again, the various other decays of the π± require the use of the hadronic field theory. Next, Santilli solved in Section 5 of the paper 1978B the structure model of the remaining mesons of basic SU(3) multiplets that will be reviewed in Section 6.2.
Along similar lines, Santilli noted that the μ± leptons admit the spontaneous decay
and showed that the structure model
provides a representation of all characteristics of the muons, as well as the compatibility with the meson decay
The existence of bound states (6.2) and (6.7) with the same number of elementary constituents but different values of the total angular momentum is a confirmation of the existence of two classes of irreducible representations of the isotopic SU*(2)-spin symmetry, called regular and irregular isorepresentations, essentially characterized by the preservation or mutation of conventional spin eigenvalues, respectively.
Following decades of extensive and solitary study on the achievement of full maturity of the Lie-isotopic theory and quantum mechanics, as reviewed in the five monographs hereon referred to as HMMC
Hadronic Mathematics, Mechanics and Chemistry, Volumes I, II, III, IV and V
R. M. Santilli, International Academic Press (2008)
Santilli reached a nonrelativistic exact representation of the neutron synthesis from a proton and an electron as occurring in stars, first presented in the 1990 paper
Apparent consistency of Rutherford's hypothesis on the
neutron as a compressed hydrogen atom
R. M. Santilli,
Hadronic J. Vol. 13, 513-531 (1990)
See also the paper he wrote while visiting the International Center for Theoretical Physics in Trieste, Italy,
Apparent consistency of Rutherford's hypothesis on the neutron structure via the hadronic generalization of quantum mechanics - I: Nonrelativistic treatment
R. M. Santilli,
ICTP preprint # IC/91/47 (1992)
published in "Santilli's 1991 Papers at the ICTP", International Academic Press (1992)
In essence, Santilli noted that the neutron admits the spontaneous decay (when isolated)
Hence, he showed that the structure model of the neutron as a bound state of a mutated proton (isoproton) and an isoelectron
provides an exact and invariant representation of all characteristic of the neutron, as well as its spontaneous decay.
The complete relativistic solution was reached by Santilli while visiting the Joint Institute for Nuclear Research in Dubna, Russia, in the 1993 paper
R. M. Santilli, Communication of the JINR, Dubna, Russia, number JINR-E4-93-352 (1993)
that was subsequently published in China
Recent theoretical and experimental evidence on the apparent
synthesis of neutrons from protons and electrons.
R. M. Santilli, Chinese J. System Engineering and Electronics Vol. 6, 177-199 (1995)
Again, the possible perception of "errors" in model (6.10) may be a manifestation of insufficient knowledge of the field. In fact, the notorious inability to reach the spin 1/2 of the neutron is solely valid under the abstraction of the proton and the electron as dimensionless points, which abstraction is manifestly questionable when the electron is totally immersed within the hyperdense medium inside the proton.
By contrast, when particles are admitted as being extended and, when in condition of total mutual penetration, are characterized by the covering Lorentz-Poincare'-Santilli isosymmetry, the spin 1/2 of the neutron is represented exactly in model (6.10) as reviewed in Section 6.3. As a matter of fact, this is the very aspect that required decades of research, including the prior construction of a covering of all branches of Lie's theory.
In the subsequent memoir of 1997
Relativistic hadronic mechanics: nonunitary, axiom-preserving
completion of relativistic quantum mechanics
R. M. Santilli,
Found. Phys. Vol. 27, 625-729 (1997)
Santilli also showed that the principles of the new structure model of unstable hadrons with conventional massive constituents applies to unstable baryons. For instance, the Λ baryon admits the decays
Therefore, he proved that the new structure model
represents all characteristics of the Λ baryon, as well as both decays in (6.11), (6.12), the remaining decays requiring hadronic field theory.
In the same 1997 memoir, Santilli worked out the new structure model for additional baryons and showed the compatibility of his structure models of mesons and baryons with known SU(3) classifications, as reviewed in the subsequent sections.
The above models are today known as Santilli structure models of hadrons and leptons, or hadronic structure models for short, where the term "hadronic" indicates the use of hadronic mechanics.
The understanding of the new structure model under consideration requires a technical knowledge of the equivalence of the two models in Eq. (6.13), since this equivalence is at the very basis of the notion of isoparticles and, therefore, directly related to the basic isosymmetries.
6.1D. Inapplicability of quantum mechanics to the structure of hadrons
Recall that the conventional Schroedinger equation at the foundation of quantum mechanics (for h = h/2π)
is exactly valid for the structure of the hydrogen atom because it represented all experimental evidence in a numerically exact way. This historical achievement was due to the large mutual distance between the proton and the electron allowing their good point-like approximation with consequential sole existence of action-at-a-distance interactions derivable from a potential, and related binding energy.
In Santilli's view,, the Schrodinger equation is inapplicable (rather than being "violated") for the structure of hadrons and leptons for numerous insufficiencies identified in 1978B (see also HMMC Vol. IV). Let us consider the energy data of the two main hadronic structure models (6.2) and (6.10), that is, for the πo
and for the neutron
Santilli has established that the Schroedinger equation is inapplicable to the above structure models for the following reasons:
1) All consistent quantum mechanical bound states A + B = C, as they occur in nuclei, atoms and molecules, have a mass defect, namely, the rest energy of the bound state C is smaller than the sum of the rest energies of the original states A and B, resulting in the very principle for which nuclear fusions release energy. The above mass defect is represented by a negative binding energy in the Schroedinger equation (6.14) for the bound state that, under these conditions, is fully consistent. By comparison, in structures (6.15) and (6.18), the rest energy of the final state is bigger than the sum of the rest energies of the constituents. As a result, any possible treatment of the structures would require a positive binding energy that is anathema for quantum mechanics because, in this case, the Schroedinger equation becomes physically inconsistent, without any known possibility of achieving solutions with the usual procedures of adding unknown parameters and the like, for the scope of adapting nature to a preferred theory.
2) It is popularly believed that the missing energy can be provided by the relative kinetic energy between the massive physical constituents. This view has no serious scientific content, because the cross section of the constituents at the missing value of the energy is extremely small (of about 10-30 barn for the pion) in which case the probability for the constituents to coalesce and form the hadron is essentially null.
3) Assuming that, via hitherto unknown manipulations, incompatibilities 1) and 2) could be resolved, simple calculations via the use of quantum mechanics show the impossibility of a quantitative representation of the meanlife of the hadron, since under the indicated conditions the hadron would decay 1010 times faster than the measured time.
4) Quantum mechanics does not allow the achievement of the spin 1/2 of the neutron via two particles, the proton and the electron, each having spin 1/2. As shown in Section 6.3, the Pauli-Fermi hypothesis of the emission of the neutrino in the neutron synthesis is far from being settled, e.g., because the mechanism for a neutron to "decompose" itself and produce the neutrino is vastly unknown, since Fermi's weak interactions provide an external description without detailed structural content.
5) Assuming that all the above incompatibilities (that are per se irreconcilable on serious scientific grounds) are somewhat resolved, quantum mechanics cannot represent the magnetic moment of the neutron from the known magnetic moments of the proton and the electron.
6) When facing the missing 0.782 MeV for the neutron synthesis, a rather popular approach is that of considering the complementary hypothesis of the anti-neutrino according to the reaction
and assuming that the missing energy is provided by the antineutrino. Santilli has pointed out that this popular belief has no serious scientific foundations because the antineutrino has a virtually null cross section with the proton and the electron. Consequently, there is no possibility that the antineutrino can deliver the 0.782 MeV needed for the neutron synthesis.
7) Santilli has additionally shown, e.g., in the paper
Does antimatter emit a new light?
R. M. Santilli,
Hyperfine interactions Vol. 109, 63-81 (1997)
that, to achieve democracy in the treatment of matter and antimatter, the anti-neutrino has to be interpreted as having a
In summary, in numerous cases of particle physics (such as the proton-antiproton annihilation of the Bose-Einstein correlation, and many other processes indicated in Chapter 5), supporters of quantum mechanics as the final theory of nature can manage to add unknown parameters, change equations with unknown functions fitted from the data, and do other procedures to claim that "quantum mechanics is valid." However, this manipulation of scientific knowledge is impossible for the synthesis of the neutron as well as of all hadrons at large because no matter what manipulation is conceived, no quantitative representation of all characteristics of the neutron and the other hadrons is possible via quantum mechanics.
6.1E. The dichotomy: classification vs structure of hadrons and leptons
As stated in the original memoirs 1978A and 1978B, in the memoir of 1981
An intriguing legacy of Einstein, Fermi, Jordan and others:
The possible invalidation of quark conjectures
in the more recent paper
Does antimatter emit a new light?
and in various additional works (see HMMC, Vol. I for a general review and references), Santilli accepts the SU(3)-color Mendeleev-type classification of hadrons as being final; he recognizes that quarks are necessary for the technical elaboration of SU(3) theories; but he identifies quarks with their technical definition, namely, as purely mathematical representations of a purely mathematical internal unitary symmetry defined in a purely mathematical, complex-valued internal unitary space.
Consequently, Santilli does not accept that quarks are physical particles for the following reasons:
1) There is no technical possibility for defining quarks in our spacetime, e.g., because of known technical incompatibilities with the Lorentz-Poincare' symmetry, with consequential impossibility a priori for quarks being physical particles in our spacetime.
2) As recalled earlier, quark conjectures require that, at the time of the synthesis of the neutron inside stars, the permanently stable proton and electron "disappear" from our universe to be replaced by hypothetical quarks and then, at the time of the spontaneous decay of the neutron, the proton and the electron simply "reappear" in our universe. Santilli believes that these views are implausible and merely based on the intent of preserving the validity of quantum mechanics inside hadrons (because the hypothetical quarks are assumed as having a hypothetical point-structure, thus being sued to maintain the validity of quantum mechanics).
3) Assuming that the above problems can be somewhat bypassed, Santilli has provided a rigorous proof that quarks cannot have gravity because, according to Einstein, gravity can solely be defined in our spacetime while quarks cannot. Consequently, in the event protons and neutrons were made up of quarks, gravity could not exist in the universe.
4) Santilli has additionally proved that the so-called "quark masses" are pure mathematical parameters thrown into the equations to adapt nature to a preferred theory, because quarks cannot have inertia since they cannot be characterized via the second-order invariant of the Lorentz-Poincare' symmetry. In the absence of a scientifically proved inertia, the notion of "quark masses" is essentially a theology.
5) Santilli has additionally disproved claims of "quark confinement" by using Heisenberg's uncertainty principle, that establishes the existence of a finite probability for free isolated quarks in dramatic disagreement with experimental evidence. This inconsistency is essentially due to the assumption of the exact validity of quantum mechanics in the outside as well as the inside of hadrons under which assumption no model can possibly render identically null the transition probability from interior to exterior states.
In Santilli's view, the biggest obstacles against the development and utilization of the energy contained in the neutron is the widespread belief that hypothetical, directly undetectable and permanently confined quarks are physical constituents of the neutron and of hadrons at large.
In the event such a conjecture is correct, and quarks are physical constituents of the neutron, no possibility exists or is conceivable for the utilization of the energy in its interior because quarks have to be assumed as being permanently confined, while all known nuclear, atomic and molecular energies are based on the capability of extracting the constituents and turning them free. On the contrary, if the electron is indeed a physical constituent of the neutron even in a mutated form, said energy can indeed be utilized, as we shall see in Chapter 7, via its stimulated decay.
Among all available alternatives to bypass the above problematic aspects, Santilli's solution proposed since 1978B (but ignored by numerous particle physicists to their peril) appears as being the most plausible one, namely, assume the standard model as the final Mendeleev-type classification of hadrons and construct a basically new model for the structure of individual hadrons of a given SU(3) family under the condition, as it was the case for nuclei, atoms and molecules, that the structure model achieves compatibility with the classification.
For the case of atoms, the transition from the Mendeleev classification to the atomic structure required the transition from classical mechanics to a new discipline, quantum mechanics. Due to the hyperdense character of the medium inside hadrons, the transition from the classification of hadrons to the structure of individual hadrons requires the transition this time from quantum mechanics for exterior conditions of point-like particles to the covering hadronic mechanics for interior conditions of extended particles in conditions of total mutual penetration.
Recall that the isotopic branch of hadronic mechanics with Lie-Santilli isoproduct [A, B]* = ATB - BTA is directly universal for all closed isolated systems, irrespective of whether with solely Hamiltonian or Hamiltonian and non-Hamiltonian internal forces, and that the genotopic branch of hadronic mechanics with Santilli Lie-admissible product (A,B)* = ARB - BSA in its single-valued and multi-valued hyperstructural realizations (Chapter 2) are directly universal for all known open-irreversible systems, thus including as particular cases isotopic and quantum theories.
Consequently, the assumption of broader non-Hamiltonian interactions for the structural problem renders hadronic mechanics uniquely and unambiguously applicable due to its direct universality, invariance over time, and covering characters. Therefore, claims that alternative generalizations of quantum mechanics (such as the so-called deformations of quantum mechanics proposed by Santilli in 1967) are "new" require the hardly achievable proofs of their novelty with respect to hadronic mechanic, equal invariance over time and covering character.
6.2. REDUCTION OF MESONS AND LEPTONS TO ELECTRONS AND POSITRONS
6.2A. Conception of the πo structure
As recalled in Section 6.1C, Santilli conceived in memoir 1978B the πo as a compressed positronium, namely, as a bound state of one electron and one positron at 1 fm mutual distance since such a conception naturally explains the charge radius of the πo, its very small meanlife (since electrons and positrons annihilate each other), its spontaneous decay
Note that the electron and the positron are permanently stable massive particles, unless they annihilate each other. Consequently, Santilli argued that the most plausible hypothesis is that the electron and the positron are the physical constituents of the πo, namely, decays (6.23) is a form of tunnel effect of the massive constituents.
The hypothesis essentially implies that the infinite quantum states of the positronium admit one single additional energy level at 1 fm distance, the πo. However, it is well known that quantum mechanics prohibits such an additional bound state. Moreover, in early 1978, Santilli had discovered the impossibility for Schroedinger equation to admit physically meaningful solutions when the rest energy of the bound state is bigger than the sum of the rest energies of the constituents, Eqs. (6.16), for which very reason Santilli proposed the construction of the covering hadronic mechanics.
R. M. Santilli,
Found. Phys. Vol. 11, 384-472 (1981).
R. M. Santilli,
Hyperfine interactions Vol. 109, 63-81 (1997)
as well as its secondary decay
where the first decay is expected from annihilation, the second decay is expected as a tunnel effect of the constituents, and the remaining decays are interpreted as their mixture or higher order processes.
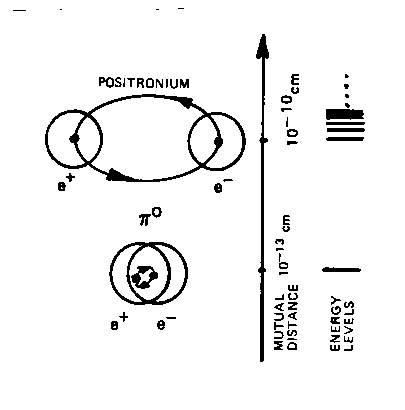
Figure 6.3: A reproduction of an original figure used by Santilli in 1978 to illustrate his model of the πo particle as "compressed positronium," namely, as consisting of one single additional bound state of the positronium under conditions of total mutual penetration of the constituents at 1 fm mutual distance verifying the covering hadronic mechanics. Santilli then showed that the model represents the totality of the characteristics of the πo, including rest energy, meanlife, charge radius, charge, spin, parity, magnetic moment and main decays.
Hence, Santilli conceived the πo as being created in the transition from the positronium (pos) verifying quantum mechanics (qm), to a new bound state at the distance of 1 fm under total mutual penetration of the wavepackets of the constituents, the πo, verifying the covering hadronic mechanics (hm), thus including the necessary singlet coupling to avoid the repulsive forces in triplet couplings for particles inside each other
Santilli realized since the early stages that, when in conditions of total mutual penetration of their wavepackets, electrons and positrons cannot be the same as when isolated in vacuum under sole long range electromagnetic interactions. He then assumed that the electron and the positron acquire a mutated form e*- and e*+ called in memoir 1978B eleton and antieleton, respectively, although the names of isoelectron and isopositron became later on more widely used due to their characterization via isosymmetries.
Still in early 1978, Santilli also argued that the conditions of mutual penetration of the constituents implies the presence of new contact, nonlinear, nonlocal and nonpotential forces that cannot possibly be represented with a Hamiltonian. This led to the conception of hadronic mechanics as a nonunitary covering of quantum mechanics and this naturally led Santilli to the quantitative representation of the "compression of the positronium" via the nonunitary map
Recall that the Schroedinger equation for the positronium represents all characteristics of the state considered. Along the same lines, Ref. 1978B proved that one single nonunitary image of Schroedinger equation represents the totality of the characteristic of the πo.
In this section we outline Santilli's structure model of the πo with physical elementary constituents and the main lines of the structure models for the remaining mesons and (unstable) leptons, as well as their compatibility with known SU(3) classifications. Regrettably, we cannot possibly review the exact analytic solution due to its advanced mathematical character. Interested readers are suggested to study Section 5 of memoir 1978B that remains the most comprehensive presentation of the topic to this day (see also the detailed review in HMMC, Vol. IV).
6.2B. Structure equation of the πo
Recall again that the Schroedinger equation for the positronium provides a numerically exact representation of all characteristics of the bound state considered. Consequently, Santilli considers a generalized equation as truly representing the "structure" of "one" given hadron if and only if it represents the "totality" of the characteristics of the hadron considered.
Other studies, such as the representation of only the mass of a hadron as part of a spectrum of masses including those of other hadrons, even though scientifically valuable, have no connection with the content of this section because, in Santilli's view, they treat the Mendeleev-type classification of hadrons and not their structure.
In the historical memoir 1978B, Santilli implemented as follows the above conception. Consider the Schroedinger equation for the positronium with electron mass m, charge -e, state |e> = |e(t, r)>, and h-bar = h,
The image of the above equations under a nonunitary transform is given by the following basic rules of hadronic mechanics
where |e*> = |e*(t, r)> represents the wavefunction of the isoelectron, ∂*r represents the isoderivative (Chapter 2), one should keep in mind that the eigenvalue E' is different than the original value E, and h is generally omitted in the equations of hadronic mechanics because absorbed by the isounit.
By using Eq. (6.30), Eq. (6.29) can be explicitly written
where one should note the absence of the isotopic element T* between the Coulomb potential and the state |e*> since, at this nonrelativistic level, the charge is not mutated and the Coulomb potential acts as a scalar (not so at the relativistic level as shown in the next section). As a result, nonunitary transform (6.29) solely acts as follows
Note that, as it is the case for the synthesis of the neutron and of all hadrons, the positronium does not naturally perform the transition to the πo particle unless there is an external action, called by Santilli the "trigger," such as collision, impact, external forces, or other means. For the case of the synthesis of the πo, Santilli represented the trigger with the Hulten potential
where K is a constant and R represents the charge radius of the considered state, resulting in the following structure equation
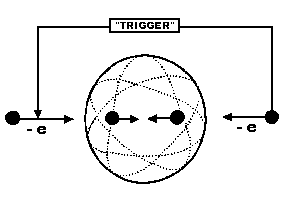
Figure 6.4: A conceptual rendering of Santilli's "trigger" consisting of an external action (such as collision, pressure, etc.) forcing particles to pass through the "hadronic horizon" (the sphere of radius 1 fm) with consequential activation of strongly attractive forces discussed in the text.
When compared to Eq. (6.26), Eq. (6.35) clearly illustrates a central feature of hadronic mechanics, the lifting of Planck's constant h into Santilli isounit
This is necessary to avoid implausible assumptions, such as the belief that an electron in the core of a star has the same quantized energy levels as when moving isolated in vacuum as a member of an atomic structure.
However, the Hulten potential is known to behave at short distances like the Coulomb potential. Therefore, Santilli assumed the following good approximation in the interior of the hadronic horizon
namely, the Hulten potential "absorbs" the Coulomb potential at short distances resulting in a mere change of the constant, from the original value K to the new value N.
Additionally, Santilli noted that, unlike the case of point particles at large mutual distances, the most stable orbit for extended particles under conditions of mutual penetration is the circle. Alternatively, it is easy to see that elliptic orbits cause the exiting of the hadronic horizon, with consequential return to a fully quantum state. This property allowed the additional good approximation
where | I*2 | stands for absolute or average value of I*2.
Hence, in Section 5 of memoir 1978B, Santilli reached the following structure model of the πo meson as a hadronic bound state of one isoelectron and one isopositron
where one should remember our assumption that h is absorbed in the isounit (see memoir 1978B for explicit expressions).
As we shall see in the next section, the single equation (6.39) achieved for the first time in scientific records the numerically exact and time invariant representation of all characteristics of the πo meson, as necessary for a true model of structure. As we shall also see, this historical achievement is permitted by the nonunitary character of hadronic mechanics combined with novel short range interactions due to total mutual penetration of the wavepackets of the constituents.
Note that the Hulten potential in Eq. (6.39a) is conventional, thus negative in value. Consequential, Eq. (6.39a) could not possibly represent the total energy of 135 MeV of the πo with 0.511 MeV constituents due to the inconsistency of the Schroedinger equation under these conditions recalled earlier. Consistency is restored by the renormalization of the rest energy (6.38) that renders Eq. (6.39a) consistent, as shown below.
In summary, Santilli proposed in memoir 1978B the construction of hadronic mechanics as a nonunitary covering of quantum mechanics, identified in the same memoir the main dynamical equations, and established the necessity of the new mechanics as the sole permitting a consistent representation of all characteristics of the πo meson.
Since 1978, model (6.39) has been re-derived in various alternative ways by several authors always resulting in Eq. (6.39a) as final structural model. We here present the following alternative derivation.
Recall that, in first approximation, the elementary charge e is not assumed as being mutated in the above nonrelativistic hadronic treatment. However, all characteristics of particles are mutated at the relativistic hadronic level, thus including the elementary charge, as necessary from the Lorentz-Poincare'-Santilli isosymmetry (see Section 6.3). Consequently, the elementary charge can indeed be considered as being mutated at the nonrelativistic level too, e ⇒ e', and, in lieu of Eq. (6.33), we introduce the following lifting
in which case the hadronic structure equation can be written
For general consistency, Santilli isounit must have the structure (with h = 1)
when F(r) is a well behaved positive-definite function, since the above realization verifies the following conditions: 1) Representation of deep mutual penetration of the wavepackets of particles at distances of 1 fm; 2) Presence of novel nonlinear, nonlocal-integral and non-potential interactions represented by the isounit, rather than the Hamiltonian; and 3) Recovering of quantum mechanics uniquely and identically outside the hadronic horizon thanks to the limit (with h = 1)
We then introduce, apparently for the first time, the following realization of the isounit
that, to first order, can be written
It is then easy to see that the replacement of value (6.46) in Eq. (6.41) recovers Eq. (6.35), hence, Eq. (6.39), identically,
The minus sign in the exponent of isounits (6.42), 96.44) has a truly crucial function deserving a mention. Recall that Planck's constant h is positive-definite but much smaller than one. Since hadronic mechanics is an axiom-preserving isotopy of quantum mechanics, the isounit must equally be positive-definite but smaller than one,
Consequently, the renormalization rest energy (6.38) is much bigger then the conventional energy, i.e.,
This is the mechanism, first identified by Santilli in 1978B, turning an inconsistent Schroedinger equation into a consistent form because, as shown in the next section, the value of 2m' is bigger than 135 MeV, thus allowing the indicial equation to have physically meaningful solutions.
6.2C. Solution of the πo structure equation.
The representation of features (6.39e) to (6.39h) is trivial for all structure models of the πo as a bound state of a particle and its antiparticle. However, it should be clarified that, as requested by the very topology and differential calculus at the foundation of quantum mechanics, the constituents of hadrons must be point-like. Consequently, quantum mechanics predicts an equal probability for both singlet and triplet bound states.
In memoir 1978B, Santilli achieved the unique representation of the spin 0 of the πo by showing that the sole stable bound state of extended particles in conditions of total mutual penetration is singlet couplings, due to extreme repulsive forces existing in the corresponding triplet coupling, and illustrated this occurrence with the so-called "gear model" (see the figure).
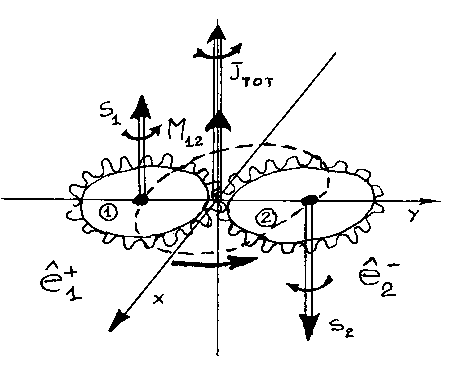
Figure 6.5: A reproduction of Fig. 2, page 852, of memoir 1978B depicting the "gear model" used to illustrate the general law of hadronic mechanics according to which, when in conditions of mutual penetration of the wavepackets and/or of the charge distributions, only singlet couplings of spinning particles are stable, while triplet couplings are highly unstable. In fact, gears can only be coupled in singlet, as shown in the figure, while their triplet coupling implies high repulsive forces. Note that this law does not exist for quantum mechanics since the particles in this case are dimensionless points, thus allowing both singlet and triplet couplings.
Consequently, Santilli restricted the analytic solution to Eqs. (6.39a) to (6.39d) reduced to their radial form (where we restore the use of Planck's constant for clarity)
where Eqs. (6.50b) to (6.50d) are not subsidiary constraints of Eq. (6.50a), but verified by the latter.
As it is well known from nuclear physics, Eq. (6.50a) admits the typical energy spectrum of the Hulten potential
where M is the maximal integer value in β2 n so that zero is lowest value of | E' |. Note that the Hulten potential has a finite number of admissible energy levels, as it is well known.
Santilli then introduces two parameters k1 and k2 defined as follows
the latter relation originating from the boundary conditions. In this case, the wavelength of the isoelectron becomes
thus being very small, and the Hulten constant can be written
thus being very large. The latter property establishes the strength of the hadronic interactions. In terms of the above parametrization, Santilli reached the following equations for the energy and the meanlife
Following due analytic process, the set of structure equations (6.50) is then reduced, rather remarkably, to the following algebraic solution in the k-parameters (see 1978B, (Eq. (5.1.32), page 840)
with numerical results
The following comments are now in order:
1) Invariant representation of all πo characteristics. As one can see, Santilli reached in 1978B the exact representation of all the characteristics of the πo with physical, that is, directly detectable massive constituents, a mutated electron (isoelectron) and a mutated positron (isopositron), including the exact representation of all intrinsic characteristics of the particle and constituents and of spontaneous decay (6.22), (6.23). The representation of the remaining spontaneous decays is based on second order effects, such as annihilation or pair creation in the interior of the πo, thus requiring the hadronic quantum field theory under development at this writing.
By comparison, the structure model of the πo as a bound state of a quark and an antiquark does indeed represent the rest energy, but as one element of a mass multiplet thus linking the structure of the πo to those of the remaining mesons of a given SU(3) multiplet. Such a characterization cannot possibly provide the joint representation of the meanlives of all members of the same multiplet, while the size of each meson remains essentially unaddressed. We therefore have a model similar to the classification of a family of atoms without any information for their quantized energy emissions and their size, with evident insufficiencies. Additionally, mesons are strongly interacting particles, thus experiencing gravity while, as indicated earlier, quarks cannot have gravity because they cannot be consistently defined in our spacetime. Moreover, the electron and the positron are believed as being "created" at the time of decay (6.23) although without a detailed quantitative representation, again, because quarks are solely defined in interior complex-values spaces, while electrons and positrons are solely defined in our spacetime. The conceptual, mathematical, physical and experimental advantages of Santilli's structure model of the πo over quark conjectures are then evident.
Besides the representation of all features of the πo, the axiomatic consistency of the model should be pointed out. In fact, the model is crucially dependent on the use of internal nonconservative and non-Hamiltonian forces, thus being nonunitary when formulated on a conventional Hilbert space over a conventional numerical field. The formulation of the model via hadronic mechanics is the only one known to the authors bypassing the Theorems of Catastrophic Mathematical and Physical Inconsistencies of Nonunitary Theories reviewed in Section 6.7, thus achieving axiomatic consistency, with particular reference to invariance over time of: numerical predictions, Hermiticity and observability that are necessary for any model to have physical value.
2) Suppression of the atomic energy spectrum. This feature is achieved by the property that , under values (6.62), the Hulten potential admits one and only one energy level, the πo because of the following maximal possible value
and the binding energy is very small,
In turn, this implies the following value of the isorenormalized energy of the isoelectron
which value is crucial for the consistency of Eq. (6.50a). As stressed earlier, the suppression of the atomic energy spectrum is crucial for the consistency of the model because any energy spectrum would imply the transition from the structure to the classification problem. Additionally, any excited state of the πo would imply exiting the hadronic horizon, thus returning to a quantum structure. Needless to say, the excited states of Santilli structure model of the πo meson are the positronium states.
3) Ignorable binding energies. The very small value of the binding energy, E' ≈ 0, should be clarified because generally believed as being inconsistent by readers with vast knowledge of quantum mechanics but insufficient technical knowledge of the covering hadronic mechanics. The forces primarily responsible for the above model are of contact, zero-range type for which the introduction of a potential, and, consequently, of a binding energy, has no physical meaning.
As indicated in the preceding section, Santilli eliminated the Coulomb interactions and absorbed them into the Hulten term because the latter is much stronger (in absolute value) than the former at short distances. However, the Hulten "potential" in Eq. (6.50a) is merely a projection of the nonpotential isounit as in Eq. (6.42). Hence, when properly formulated on a iso-Hilbert space over an isofield, Santilli structure model of the πo shows no potential at all. Hence, the value E' ≈ 0, rather than being inconsistent, is necessary for the consistency of the model.
It is evident that, having opposite isocharges, the isoelectron and the isopositron attract each other according to the Coulomb law, thus having indeed a non-null negative binding energy. The point is that such an enlargement, that is, the solution of Eq. (6.35) rather than (6.50a), was not considered by Santilli in 1978B and its study has remained left to interested readers to this day. Note that the low value of the binding energy is in line with models of the so-called "asymptotic freedom."
4) Strongly attractive hadronic couplings. One of the most scientifically productive features of the above structure model has been the identification of strongly attractive contact forces between particles when in singlet couplings under conditions of overlapping of their wavepackets or their charge distributions. This force has been crucial for the conception and industrial development of new clean energies studied in the next chapter.
5) Charge independence of strong interactions. Another central point in Santilli's structure model of hadrons is that, unlike electromagnetic interactions, strong interactions are primarily characterized by (nonlinear, nonlocal-integral and) nonpotential interactions he represents with the isounit. Such a conception is necessary, in any case, for the consistency of the model here considered because, as well known, the πo meson is a strongly interacting particle.
But one of the main features of strong interaction is their charge independence. Consequently, A. O. E. Animalu pointed out in the memoir
A. O. E. Hadronic J. Vol. 16, page 411 (1993)
that the contact interaction characterized by the Hulten force is so strong to overcome Coulomb repulsion between identical electrons resulting in the birth of a broader formulation of superconductivity and related Cooper pair studied in Chapter 5. Subsequently, Santilli and Shillady realized that the same force is responsible for the strength of valence electron pairs, as presented the paper
A new isochemical model of the hydrogen molecule
R. M. Santilli and D. D. Shillady,
Intern. J. Hydrogen Energy Vol. 24, pages 943-956 (1999)
by achieving the first known exact representation of molecular binding energies from unadulterated first principles.
6.2D. Structure model of unstable leptons and of the remaining mesons.
Next, Santilli provided in memoir 1978B a quantitative analytic solution of the following structure models of unstable leptons and of the remaining light (unflavored) mesons based on Assumptions 1-5 of Section 6.1C:
Let us consider first the three-body hadronic bound state models (6.67a) and (6.67b). The first difficulty in the acceptance of these models is the need to abandon quantum mechanics in favor of covering hadronic mechanics due to the impossibility of the former to represent the rest energies of the particles considered, as it was the case for the πo. However.
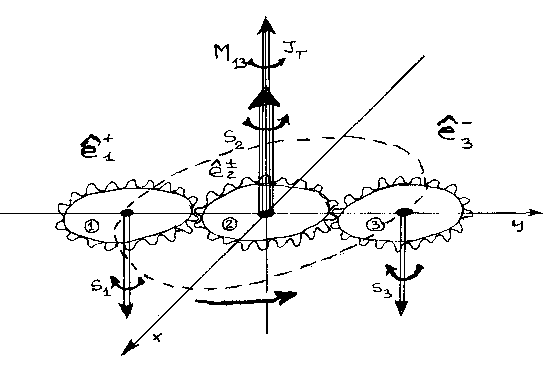
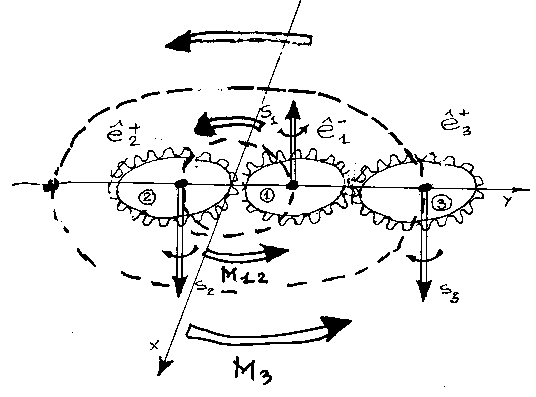
Figure 6.6. Reproduction of the original figure used by Santilli in Section 5 of the memoir 1978B to illustrate the dynamical differences between his structure model of the μ± (top view) and of the π± (bottom view). In the former case, we have an isoelectron e± at the center and two isoelectrons orbiting around, thus requiring no mutation of the angular momentum to represent the spin 1/2 of the muons. In the latter case, we have a πo at rest in the center (since it is much heavier than the electron) with an isoelectron e± orbiting within the πo structure (since the size does not increase appreciably in the transition from the πo to the π±). In the latter case, a mutation of the total angular momentum of the isoelectron is necessary to represent the spin 0 of the π± mesons. These two different values of the spin under the same number of elementary constituents are an excellent verification of the regular and irregular isorepresentations of the Lie-Santilli SU(2) spin symmetry outlined in the next section for the structure of the neutron. As we shall see, the two cases here considered are interpreted by Santilli as providing a direct distinction between electroweak and strong interactions (see HMMC Vol. III for details and references).
Additionally, we see the emergence of the following new difficulty. Model (6.67a) readily represents the spin of the muons, while there is no possibility for quantum mechanics to represent the spin 0 of the π± mesons as bound states of three particles each having spin 1/2 when in vacuum. Consequently, models (6.67) were generally dismissed by the physics community of the late 1970s because impossible under Lie's theory. This caused a significant scientific impasse in hadron physics, including decades of delays in the conception and industrial development of much needed new clean energies (studied in the next chapter), since the latter are crucially dependent on deviations from quantum mechanics within hadronic media.
In our view, the above impasse was justified in 1978 since, at that time, Santilli had just proposed the isotopies of Lie's theory in the preceding memoir1978A. Moreover, said isotopies were presented as particular cases of the broader Lie-admissible genotopies of Lie's theory for irreversible conditions, thus dealing with a mathematical level beyond that of the general physics audience of the time.
Despite the lack of general acceptance of his structure model of hadrons, Santilli spent decades of solitary studies to develop in all details the theory nowadays known as the Lie-Santilli isotheory, with particular reference to the isotopies of the SU(2)-spin symmetry and its isorepresentations (reviewed in Chapters 2 and 3), by showing in the 1990s that model (6.67b) can indeed represent the spin 0 of the π± mesons in a fully consistent way, provided one accepts the existence within hyperdense hadrons of nonlinear, nonlocal and non-Hamiltonian interactions beyond any dream of representation via Lie's theory.
As a matter of fact, Santilli noted in memoir 1978B that the problem of the spin of the π± is essentially equivalent to that of the spin of the neutron when interpreted as a bound state of a proton and an electron because, in both cases, there is the need of the mutation of spin in addition to that of the rest energy. To follow the historical evolution, we shall review the mutation of spin in the next section, as originally achieved for the structure of the neutron. In this section, we shall limit ourselves to a review of the original presentation in memoir 1978B.
In regard to model (6.67a), Santilli states: With all due respect to different views by my colleagues, I could never accept the hypothesis that muons are elementary because they are naturally unstable with spontaneous decays releasing electrons and positrons. Hence, the most natural hypothesis is to assume that the muons are bound states of electrons and positrons. The decay mode
suggested that muons are three-body bound state of an electron-positron pair plus an electron, since such a structure allows the representation of muons rest energy, spin, meanlife, magnetic and electric dipole moments and decays via electron-positron annihilation or other processes. As well known, such a conception is utterly inconsistent for quantum mechanics due to the inability of Schrodinger's equation to represent the muon rest energy. Rather than restraining my studies, such an inconsistency provided additional reasons to build a new mechanics specifically conceived for the structure of unstable particles, so as to prevent the adaptation of physical reality to a preferred theory.
The main characteristics of the μ± are the following:
In Section 5 of memoir 1978B, Santilli provided an exact analytic solution of model (6.67a) via its reduction to a restricted three body system that reproduced the analytic treatment of the preceding sections, resulting in the following numerical values of the characteristic k-quantities:
that should be compared with the corresponding values (6.62).
Note that k2 is bigger than, but very close to 1. Hence, structure model (6.67a) also suppresses the atomic spectrum, this time, of the helium, down to one single energy level, that of the muon. It was noted in memoir 1978B that the above values were computed for the charge radius of the muon R = 10-19 cm and that, R ⇒ 0 implies k2 ⇒ 1.
The rest energy of the muon, as well as other features, such as the differences in magnetic and electric dipole moments between muons and electrons were interpreted via a mutation of the central isoelectrons e*±, thus confirming the need for hadronic mechanics. The argument is that deformations of the shape of charged spinning bodies are known in classical mechanics to cause corresponding deformations of magnetic moments. Santilli then argued that the central electron in structure (6.67a) must experience a deformation of its wavepacket due to its immersion within those of the other electrons, with consequential, inevitable alteration (mutation) of the intrinsic magnetic moment.
Decay (6.68) is interpreted as hadronic tunnel effect of the constituents along the same lines as for the π
In regard to model (6.67b), Santilli states: Again with due respect to different view by my colleagues, I could not accept that the π± mesons have the same number of constituents of the πo, because the latter admits the spontaneous decay into an electron-positron pair, while the former admits the dominant decay
The main characteristics of the π± as the following:
Primary decay (6.77) is considered the strongest evidence in support of the models for both pions and muons. In fact, strong spin-orbits couplings as needed for the spin of structure (6.67b) are unstable, thus implying the dominance of decay process (6.77) where there is no such strong spin-orbit coupling. The hadronic interpretation of the remaining decays is also possible, and left to interested readers.
In regard to structure models (6.67c)-(6.67e), Santilli states: In the structure models of the remaining light mesons I encountered the following new scenario. The preservation of the charge radius with the increase of the mass prevented the introduction of hadronic excited states, thus forcing the total immersion of new constituents into preceding structures. On one side, this provided a great exemplification of the calculations, since all light mesons could be reduced to two-body structures essentially similar to that of the πo. However, the increase of the density caused a multiplication of internal process requiring hadronic field theory that is not yet available, resulting in a number of alternatives in need of specific studies.
As an example, following the two elementary massive constituents for the πo and three constituents for the π±, it was natural for me to assume in 1978 that the η meson is a bound state of two mutated πo. However, the η admits the decay
thus suggesting that the π± are mutated forms of μ±. But the structure model of μ± requires a three-body structure. This occurrence left no other alternative than the increase of the number of constituents by one in the transition from πo to π±. Similar inspections of spontaneous decays of other unstable hadrons and leptons then lead to the rule according to which the number of elementary massive physical constituents of unstable particles increases with mass.
By reducing the three-body structure to the two-body form ( Eq. 6.67b), and the use of the treatment of the preceding sections, memoir 1978B provided another exact analytic solution resulting again in the invariant representation of all the characteristics of the π± with the sole exception of the spin that was deferred to studies following the development the isotopies of Lie's theory. In particular, memoir 1978B found the following numerical values of the characteristic k-quantities
that should be compared with values (6.62) and (6.76).
and other decays suggesting a higher number of elementary constituents. The new aspect is that the above decays are no longer final indication of the number of elementary constituents because, with the increase of the density of the medium inside hadrons, there is the emergence of a host of basically new events, such as the creation of electron-positron pairs that, within the environment considered, are the πo, resulting in the following equivalence
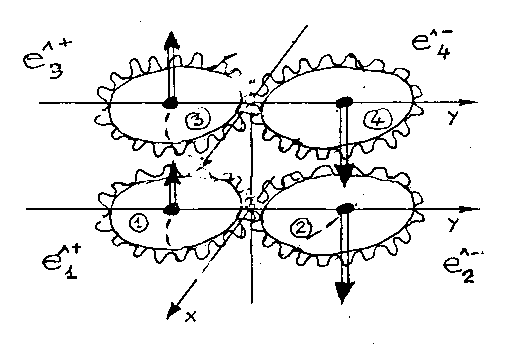
Figure 6.7: Reproduction of the original figure of memoir 1978B to illustrate the structure model of the η meson with four elementary massive constituents. Note the "compression" of two π*o one inside the other.
A similar situation holds for the K± that I considered in 1978 as being a five-body bound state of elementary massive constituents, or a two-body bound state of two mutated pions, or a two-body bound state of a mutated η meson and an isoelectron.
Again there is no contradiction with decays of the type
due to the creation of pions and other particles within the structure.
Finally, by following the same lines, it was also natural for me in 1978 to assume that the KoS and the KoL have six elementary massive constituents, thus being composed of three mutated πo. Their differences was then reduced to dynamical differences similar to those existing for μ± and π±, namely, we have the first possibility with one π*o at the center and two π*o orbiting in its interior, and the second possibility with two π*o coaleshed into the η* and the remaining π*o orbiting in its interior.
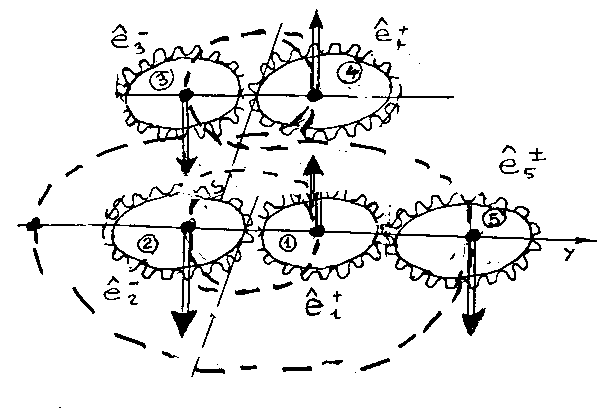
Figure 6.8. Reproduction of the original figure of memoir 1978B illustrating the structure model of the K± with five constituents.
All in all, I believe that the complexity of the events within the hyperdense hadronic medium is beyond our imagination at this writing, let alone our capacity of their analytic treatment. This aspect is best illustrated by the mystery of the origin of the 0.872 MeV missing in the synthesis of the neutron in the core of stars. Rather then being a drawback, these difficulties should intrigue true researchers with young mind of any age.
With the above clarifications, we shall assume models (6.67) as representative of the capabilities of Santilli's structure model of hadrons with elementary, physical, massive constituents, by leaving open their detailed study for interested colleagues. What is important for this presentation is that Santilli reduction of unstable leptons and light mesons to electrons and positrons is indeed plausible and does indeed provide an exact representation of all characteristics of the considered particles and their decays much beyond any possible representation with quark conjectures.
6.2E. Revisions due to the isodual theory of antimatter
In the preceding sections we have reviewed Santilli's structure model of unstable leptons and mesons as conceived in 1978. It is important to indicate that the sole significant advance since that time known to the authors has been the subsequent advent of the isodual theory of antimatter also due to Santilli, as reviewed in Section 3.7, see the comprehensive treatment in the 2006 monograph
Isodual Theory of Antimatter, with Applications to Antigravity, Grand Unification and Cosmology,
R. M. Santilli,
Springer (2006)
which is based on the operation of isoduality consisting of an anti-Hermiticity map applied to the totality of the formalism of matter, from numbers to first quantization.
As the reader may recall, the new theory was motivated by the historical imbalance of the 20th century between matter and antimatter, matter being treated at all levels of study from Newton to second quantization, while antimatter was solely treated at the level of second quantization. Santilli's isoduality has resolved this historical imbalance, by allowing the treatment of both, matter and antimatter, at all levels of study, from Newton to second quantization, in full scientific democracy.
The implications of this new formulation of antimatter are important for the hadronic structure model of particles and can be indicated as follows. By denoting the electron with the symbol e, the isoelectron with the symbol e* and their isoduals (antiparticles) with the symbols ed and e*d, model (6.2) should be written more correctly
and the same rules applies for all antiparticles. Far from being trivial, the reader should be aware that the isodual theory avoids the second quantization, thus allowing the treatment of anti-isoparticles at the level of first hadronization under a total democracy between particles and antiparticles.
Additionally, Santilli has discovered a new important symmetry verified by Dirac's equation as well as by the entire universe at the limit of equal matter and antimatter. It is given by the isoselfduality, namely, by the invariance under isoduality. The πo particle is isoselfdual because it is composed by a particle and its antiparticle. However, its decay into two γ, (Eq (6.3)) is inconsistent because it violates isoselfduality, thus confirming the insufficiency of 20th century particle physics in regard to antiparticles. In fact, the correct formulation of the πo decay is the following one verifying isoselfdual invariance on both sides
that, alone, is sufficient to illustrate the experimentally detectable inequivalence of photons produced by matter and antimatter, a feature that has stimulated the birth of the new field of antimatter astrophysics.
It is an instructive exercise for the interested reader to reformulate the preceding structure models of leptons and hadrons in the remaining aspects involving antiparticles and identify the nontrivial consequences.
6.2F. Compatibility of the new structure model of hadrons with unitary classifications
The compatibility of the structure model of mesons with physical, massive, and elementary constituents and the SU(3) classifications was worked out in Section 3.15 of the 1997 memoir
Relativistic hadronic mechanics: nonunitary, axiom-preserving
completion of relativistic quantum mechanics
R. M. Santilli,
Found. Phys. Vol. 27, 625-729 (1997)
Said compatibility is conceptually simple, but mathematically quite advanced since it requires the multi-valued hyperstructural lifting of the Lie-Santilli isotheory indicated in Chapter 2.
Let us recall the basic meson octet as characterized by the SU(3) symmetry (see Figure 6.9) which, by indicating anti-quarks with a dash, can be written
A basic implication of hadronic mechanics is that different hadrons are characterized by different isounits. Consequently, in the 1997 memoir, Santilli proposes the identification of the octet of light mesons via the total isounit
The proposed compatibility between the hadronic structure model and the SU(3) classification is then achieved via the isotopic lifting of the SU(3) symmetry with respect to the above total isounit since the latter is known to be isomorphic to SU(3), thus preserving all features of the latter, including the numerical predictions. For the study of the hyperstructural branch of hadronic mechanics we refer the interested reader to the 2005 monographs.
"Elements of Hadronic Mechanics", Vol. I: "Mathematical Foundations"
R. M. Santilli, Ukraine Academy of Sciences (1995),
"Elements of Hadronic Mechanics"
Vol. II: "Theoretical Foundations"
R. M. Santilli, Ukraine Academy of Sciences (1995)
"Isotopies, Genotopies and Hyperstructures and their applications"
R. M. Santilli and T. Vougouklis, contributed memoir in New Frontiers in Hyperstructures, Hadronic Press (1996).
The significant of the above hyperformulations of the SU(3) symmetry is that of identifying quarks as they really are, purely mathematical objects defined on purely mathematical internal spaces without connection to our spacetime. In fact the u, d, s quarks characterized by hyperunit (6.93) are regular hyperrepresentation of SU(3) that remain three-dimensional, although but 8-valued, thus without any possibility of definition in our spacetime.
6.2G. Experimental verifications
In Santilli's view, the most significant direct experimental verification of the hadronic structure model of unstable leptons and mesons is that it represents all intrinsic characteristics of the particles and their spontaneous decay, thus achieving a representation of experimental data not possible for quark conjectures, such as the representation of meanlives, charge radius, and other features.
The most significant indirect experimental verifications are the following. The hadronic structure model considered in this section is centrally based on the inapplicability of special relativity and quantum mechanics in the interior of hadrons, inapplicability that is nowadays supported by rather vast experimental evidence reviewed in Chapter 5.
It is sufficient to indicate in this respect the recent experimental evidence of deviation from the Doppler's law within physical media
Experimental verification of isoredshift with possible absence of universe expansion, big bang, dark matter and dark energy
R. M. Santilli, The Open Astronomy Journal, in press Vol. 3 (2010).
that, alone, establishes the inapplicability of special relativity within physical media at large, thus including the hyperdense media inside hadrons, in favor of Santilli isorelativity. This occurrence, alone, establishes the inapplicability in the interior of hadrons of relativistic quantum mechanics in favor of the covering relativistic hadronic mechanics. The structure model of unstable particles studied in this section then follows uniquely and unambiguously due to the direct universality of the covering theory.
Independently from all the above, the reader should remember that the studies presented in this section are based on the isotopic branch of hadronic mechanics, thus being limited to processes that are reversible over time (invariant under time reversal). Note that such a restriction is fully permitted by the basic assumption that the constituents of hadrons are massive particles produced free in the spontaneous decays.
However, the most significant decays are irreversible over time, thus preventing the use of quantum mechanics due to its reversible structure, and mandating the use of the irreversible Lie-admissible branch of hadronic mechanics.
In summary, we can conclude by saying that the hadronic structure model of unstable leptons and light mesons presented in this sections is supported by a rather significant number of conceptual, mathematical, theoretical, and experimental evidence.
6.3. REDUCTION OF BARYONS TO PROTONS AND ELECTRONS
6.3A. Conception of the neutron structure
As recalled earlier, Santilli accepted Rutherford's original conception of the neutron as a "compressed hydrogen atom" in the core of stars, identified the reasons for the impossibility by quantum mechanics to represent such a natural conception, and proposed the construction of the covering hadronic mechanics for its quantitative study.
Following a lifelong preparatory research outlined in this volume, Santilli was finally able to achieve the first known nonrelativistic, numerically exact, and invariant representation of "all" characteristic of the neutron as a hadronic bound state of a proton and an electron in the historical paper (hereon referred to as the "1990 paper")
Apparent consistency of Rutherford's hypothesis on the
neutron as a compressed hydrogen atom
R. M. Santilli,
Hadronic J. Vol. 13, 513-531 (1990)
as well as in the ICTP paper (referred to as the "1992 paper")
Apparent consistency of Rutherford's hypothesis on the neutron structure via the hadronic generalization of quantum mechanics - I: Nonrelativistic treatment
R. M. Santilli,
ICTP preprint # IC/91/47 (1992)
published in "Santilli's 1991 Papers at the ICTP", International Academic Press (1992)
Subsequently, while visiting the Joint Institute for Nuclear Research in Dubna, Russia, Santilli achieved the first known relativistic, numerically exact, and invariant representation of "all" characteristics of the neutron in its synthesis from a proton and an electron inside stars in the paper (referred to the "1993 paper")
Recent theoretical and experimental evidence on the apparent
synthesis of neutrons from protons and electrons.
R. M. Santilli, Communication of the JINR, Dubna, Russia, number JINR-E4-93-352 (1993)
subsequently published in China while visiting the Academia Sinica in Beijing, in the paper (referred to as the "1995 paper")
Recent theoretical and experimental evidence on the apparent
synthesis of neutrons from protons and electrons.
R. M. Santilli,.
Chinese J. System Engineering and Electronics Vol. 6, 177-199 (1995)
The most comprehensive studies were provided in the monographs (referred to as HMMC)
Hadronic Mathematics, Mechanics and Chemistry, Volumes I, II, III, IV and V
R. M. Santilli, International Academic Press (2008)
Among various independent studies, an excellent review is that by J. Kadeisvili in the memoir
The Rutherford-Santilli neutron
J. V. Kadeisvili,
Hadronic J. Vol. 31, 1-114 (2008)
Santilli main concretion of the neutron structure is expressed via nonrelativistic and relativistic nonunitary liftings of the conventional treatment of the hydrogen atom (hereon denoted "ha") with quantum mechanics (qm) into the corresponding forms of hadronic mechanics (hm),
where asterisk denotes the lifting of protons and electrons into isoprotons and isoelectrons, respectively, more technically realized via the transition of unitary irreducible representations from the Galilei symmetry to the Galilei-Santilli isosymmetry at the nonrelativistic level and from the Lorentz-Poincare' symmetry to the covering Lorentz-Poincare'-Santilli isosymmetry at the relativistic level.
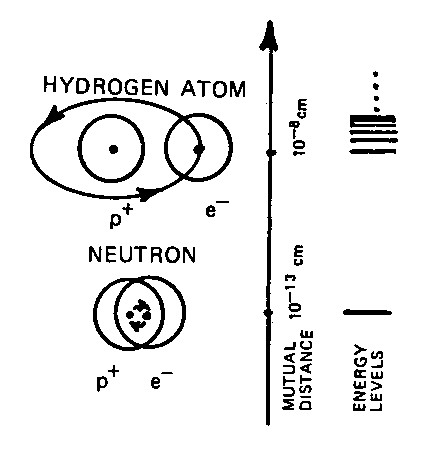
Figure 6.10: The sole bound state of a proton and an electron predicted by quantum mechanics is the hydrogen atom, with smallest orbit of the order of 10-8 cm. Thanks to the use of hadronic mechanics, Santilli has identified the existence of one and only one additional bound state, the neutron, characterized by the electron orbiting within the proton structure at distances of the order of 10-13 cm or less. Remarkably, Santilli has proved that the hadronic state is one and one only because, when excited, the isoelectron leaves the proton structure, thus recovering all conventional quantum states. In this sense, the energy levels of the hydrogen atom are the excited states of the neutron. As we shall see, these notions are at the foundation of the new hadronic energy studied in Chapter 7.
In this section we provide a review of the nonrelativistic and relativistic treatments in a form accessible to the general physics audience. However, it should be indicated again that a serious understanding of these achievements requires a technical knowledge of the entire studies because all deeply interconnected in a direct or indirect way to the neutron structure.
6.3B. Nonrelativistic exact and invariant representation of the neutron rest energy, meanlife and charge radius
The original 1990 derivation of the exact and invariant nonrelativistic representation of the rest energy, mean life and charge radius of the neutron follows very close that of the πo presented in the preceding section and, therefore, we shall review it only in its main aspects. The basic model is the familiar Schroedinger's equation for the structure of the hydrogen atom (for h = h/2π)
where |e> = |e(t, r)> represents the conventional Hilbert state of the hydrogen atom. Since the proton mass is about 2,000 times bigger than the electron mass, Santilli assumes in first nonrelativistic approximation that the proton is at rest in the neutron structure and it is not mutated, thus studying the particular case
The next step is to subject Eqs. (6.96), (6,97) to a nonunitary transforms by reaching again the main equations of hadronic mechanics,
where m' is the isorenormalized rest energy of the electron as in Eq. (6.38) and E' is the isorenormalized binding energy due to the transition from the Hamiltonian H to the new operator H*T*. At this point, the 1990 paper introduces the trigger since the hydrogen atom cannot spontaneously change into the neutron unless there is a sufficient external action. In this case, the extreme pressures in the center of a star are represented again with the Hulten potential, resulting in the modified hadronic equation
The Coulomb potential is again absorbed into the much stronger Hulten potential inside the hadronic horizon, and the coupling of the proton and the electron is necessarily assumed as being in singlet, resulting in this way in the nonrelativistic structure equation of the neutron for the rest energy, mean life and charge radius similar to those for the πo, Eq. (6.50),
The 1990 paper then studies in detail the analytic solution, by recovering the finite spectrum of the Hulten potential,
Differential equation (6.103) were then turned into the algebraic equations
where the expression 0 ≤ ε < 1 originates from the boundary conditions. In this case the Hulten constant becomes
because k2 is very close to 1. As we shall soon see, the above expression establishes that the value of V is rather large. In turn, this establishes the strength of the strong nonpotential interactions.
In this way, by plotting the numerical values, Santilli reduces Eqs. (6.103) to the solution of the following algebraic equations in the k-parameters
with numerical value for the neutron
that should be compared to the corresponding values (6.62) for the πo.
Again, as it is the case for the πo, numerical values imply the suppression of the quantum spectrum of energy of the hydrogen atom down to one energy level only, that of the neutron. Again model (6.103) admits excited states, but they cross the hadronic horizon, thus being fully quantum. Consequently, in Santilli's view, all known quantized level of the hydrogen atom are excited states of the neutron.
A result achieved by the 1990 of primary importance for new clean energies (see Chapter 7) is that the binding energy E' is very small, as expected from the "nonpotential" character of the primary binding force, as a result of which the total energy of the isoelectron is given by
As we shall see, the reduction of the neutron to a hadronic bound state of a proton and an electron has far reaching implications for all quantitative sciences, e.g., because nuclei can now be reduced to isoprotons and isoelectrons as shown in Section 6.5. The reduction also has far reaching industrial implications, e.g., because the isoelectron can be stimulated to exit the neutron, thus permitting the utilization of the inextinguishable clean energy inside the neutron as outlined later on in this section.
In closing this section, we should indicate that the above model has been reinspected since 1990 various times. A reinspection worth mentioning is that by Animalu and Santilli of 1996
Nonlocal isotopic representation of the Cooper pair in superconductivity,
A. O. E. Animalu and R. M. Santilli
Intern. J. Quantum Chemistry Vol. 29, 185 (1995)
who re-derived Eq.s (6.103) via the use of the following realization of the isounit
that can be written
where |e> is the wavefunction of the ordinary electron and |e*> is that of the isoelectron. This re-interpretation illustrates again the desired character of hadronic mechanics as being nonlinear in the wavefunctions, yet reconstructing linearity on isospaces over isofield (isolinearity). The nonpotential character of the interactions represented with the isounit is self-evident and needs no additional comments.
For clarity, we should indicate that isounit (6.113) is different than our form (6.44) because the charge was mutated in the later realization, while it was left unchanged in the former.
6.3C. Nonrelativistic, exact and invariant representation of the neutron spin.
The 1990 paper then considers the initiation of Rutherford's compression of the electron within the proton in singlet coupling, as illustrated in Figure 6.11. It is evident that, as soon as the penetration begins, the electron is trapped inside the hyperdense, much heavier and spinning proton, thus resulting in a constrained orbital motion. This is due to the fact indicated earlier that the proton is about 2,000 times heavier than the electron, as a result of which the proton can be assumed in first approximation as remaining at rest and un-mutated in its intrinsic angular momentum, while contributions from the proton mutations can at best be of second order or of relativistic character.
In this way, Santilli reached the conclusion in the 1990 paper that, under the geometry of Rutherford's compression, the electron is constrained to have an orbital angular momentum equal to the proton spin, namely an angular momentum with the value 1/2, yet opposite to the electron spin. Therefore, the spin of the neutron coincides with that of the proton.
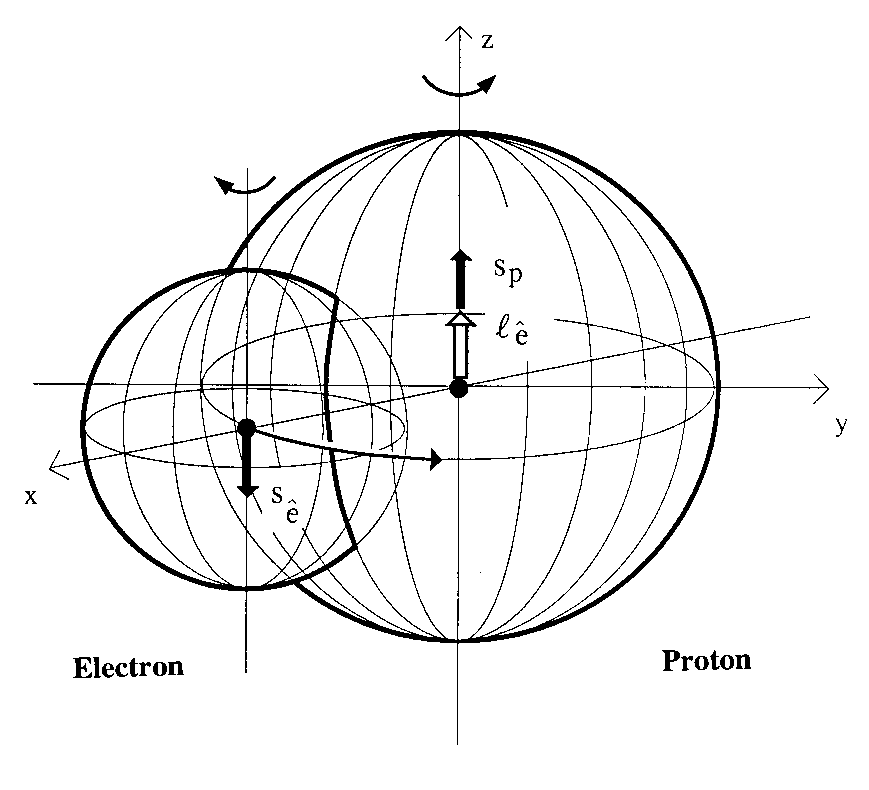
Figure 6.11: A reproduction of Figure 1 of Santilli 1990 on the spin of the neutron as permitted by hadronic mechanics. The main feature is the abandonment of the abstraction of the proton either as a point, or as a sphere with isolated points in its interior, as necessary for the applicability of quantum mechanics, and the representation of the proton as it is in the physical reality, a sphere of about 1 F in radius containing one of the densest media measured in laboratory until now. Then, at the initiation of "Rutherford's compression" of the electron inside such hyperdense medium, it is evident that the electron is captured and constrained to rotate around the proton with an angular velocity equal to the proton spin. But the electron and proton can only couple in singlet for stability. It then follows that the total angular momentum of the isoelectron is null and the spin of the neutron coincides with the spin of the proton.
It should be stressed that the above interpretation of the neutron spin is prohibited by quantum mechanics because angular momenta can only have integer eigenvalues. This is due to the fact that half-odd-integer angular momenta imply the breakdown of the unitarity of the theory, with a consequential host of problems, including the loss of causality and probability laws (see the Theorems of Catastrophic Inconsistencies of Nonunitary Theories of Section 3.9).
However, integer angular momenta were solely established for particles moving in empty space. Their supine acceptance as being also valid for a particle orbiting within a hyperdense medium without a serious scrutiny is deprived of scientific value. Also, constrained systems are well known in classical and quantum mechanics to imply anomalous eigenvalues. Finally, hadronic mechanics was constructed precisely for the regaining of unitarity on isospaces over isofields (Chapter 2). Therefore, half-off-integer angular momenta are quite natural for the covering hadronic mechanics because permitted by the Lie-Santilli isotheory, as shown below.
The exact and invariant representation of the spin 1/2 of the neutron was first achieved in the 1990 paper, which also provides the resolution of related consistency problems. This first derivation can be summarized as follows.
Let |s> be the conventional two-dimensional basis of the SU(2) spin symmetry with generators Jk, k = 1, 2, 3, conventional commutator rules and eigenvalues. Santilli applies in the 1990 paper the isotopic lifting of the SU(2) symmetry worked out previously (characterized by the following isounit, isotopic element, isocommutation rules and isoeigenvalues)
where M and N will be identified shortly, and condition (6.119) is needed to assure isounimodularity. A realization of the above SU*(2) Lie-Santilli isoalgebra is given by
with isoeigenvalues
with corresponding liftings for three- and higher-dimensional cases (that require isounits of corresponding dimensions) here omitted for brevity.
It is evident that the above isotopic SU*(2)-spin symmetry characterizes the following mutations of spin S and angular momenta L for an electron within the hyperdense medium inside the proton,,
where Q is the equivalent of P in the three-dimensional isotopy of SU(2) for the case of the angular momentum. Note that hadronic mechanics remains isounitary for all the above infinitely possible eigenvalues of spin and angular momenta, thus including fractional values of angular momenta as a particular case of a much broader class.
The spin of the neutron is given by the sum of the isotopic realizations of the intrinsic and orbital angular momentum of the proton and isoelectron with isoeigenvalues (see the 1990 paper for details)
Since the proton is much heavier than the electron, it can be considered at rest in first approximation, thus having conventional (quantum) spin 1/2 as indicated in Figure 6.11. Also, as indicated earlier, the electron can only have a stable coupling with the proton in singlet. Therefore, the electron has spin -1/2 in the configuration of Figure 6.11. It then follows that the only possible solution is that indicated earlier, for which the spin of the neutron coincides with that of the proton, and the isoelectron has null total angular momentum.
The invariant isounitary representation of the spin of the neutron via the isotopies of SU(2)-spin is then characterized by the values (see again Santilli's 1990 paper for details)
It should be noted that in a more realistic model all angular momenta of the electron and of the proton are mutated, thus implying eigenvalues that are not necessarily integer or half-off-integer.
Note also the necessity of the isotopies for the achievement of an exact and invariant representation of the spin of the neutron. Note finally the direct universality of the above isotopies of SU(2)-spin, in the sense that any other nonunitary realization is equivalent to the preceding one.
6.3D. Nonrelativistic, exact and invariant representation of the neutron magnetic moment
In this section we review the original, nonrelativistic, exact and invariant representation of the magnetic moment of the neutron,
from those of the proton and of the isoelectron also achieved for the first time in Santilli 1990.
Recall from the preceding sections that: the spin of the neutron coincides with that of the proton; the isoelectron's spin is antiparallel to that of the proton; and the orbital angular momentum of the isoelectron is parallel to that of the proton spin, yet the magnetic moment it creates is antiparallel due to the negative charge. Recall also that the intrinsic magnetic moment of the electron when isolated in vacuum is much bigger than that of both the proton and the neutron because
The magnetic moment of neutron is characterized by three contributions: the magnetic moment of the proton; that of the isoelectron; and that caused by the orbital motion of the isoelectron. Note that the third contribution is completely missing in quantum mechanics because all particles are considered as massive points, in which case the electron cannot rotate inside the proton. As Santilli states: I believe that the inability by quantum mechanics to treat the orbital motion of the electron inside the proton, with consequential failure to represent the anomalous magnetic momentum of the neutron, was the very origin of the conjecture of the neutrino.
With reference to the orientation of Figure 6.11, and by keeping in mind that a change of the sign of the charge implies a reversal of the sign of the magnetic moment, the derivation of Santilli 1990 is based on the identity
Since the spin of the proton and of the electron can be assumed to be conventional in first approximation, we can assume that the magnetic moments of the proton and of the isoelectron are conventional, i.e.,
It is then evident that the anomalous magnetic moment of the neutron originates from the magnetic moment of the orbital motion of the isoelectron inside the proton, namely, a contribution that has been ignored since Rutherford's time until treated in Santilli 1990.
It is easy to see that the exact and invariant representation of the anomalous magnetic moment of the neutron is characterized by the following numerical values
and this completes our review of the nonrelativistic representation of the neutron characteristics. Note that the small value of the total magnetic moment of the isoelectron is fully in line with the small value of its total angular momentum (that is null only in first approximation due to the assumed lack of mutation of the proton).
6.3E. Foudations of the relativistic treatment
Santilli achieved the first relativistic invariant and exact representation of all characteristics of the neutron as a "compressed hydrogen atom" in the 1993 paper written while visiting the Joint Institute for Nuclear Research in Dubna, Russia,
Recent theoretical and experimental evidence on the apparent
synthesis of neutrons from protons and electrons.
R. M. Santilli, Communication of the JINR, Dubna, Russia, number JINR-E4-93-352 (1993) published in the
Chinese J. System Engineering and Electronics Vol. 6, 177-199 (1995)
The achievement was based on preceding extensive studies on theisotopies of the Minkowski space, the Lorentz-Poincare' symmetry and special relativity summarized in the 1991 monographs (see HMMC Vol. III for a 2008 update)
"Isotopic Generalization of Galilei and Einstein Relativities",
Volume I: "Mathematical Foundations"
R. M. Santilli,
Hadronic Press (1991)
"Isotopies of Galilei and Einstein Relativities"
Vol. II: "Classical Foundations"
R. M. Santilli,
Hadronic Press (1991)
In his 1993 paper, Santilli achieved the first correct and time invariant isotopies of Dirac equation, and proved its validity by providing the indicated relativistic representation of the neutron synthesis.
Relativistic hadronic mechanics and the isotopies of Dirac equation have been outlined in Section 3.11Q. We discourage the reader from inspecting this section without an in depth knowledge of relativistic hadronic mechanics to prevent the possible illusion of valid criticisms. We merely recall for notational scopes that relativistic hadronic mechanics requires at least two isotopies, one for spacetime and one for spin, plus possible additional isotopies, e.g., for internal isounitary symmetries (see later on in this chapter). These isotopies are uniquely characterized by the Lie-Santilli isotheory with the two isounits (3.221), e.g.,
The isounit for spacetime (st) characterizes the Minkowski-Santilli isospace and the isospinorial Lorentz-Poincare'-Santilli isosymmetry, while the spin isounit characterizes the isotopic spin symmetry.
The isolinearization of the second order isoinvariant then yields the invariant isotopies of Dirac's equation, today known as the Dirac-Santilli isoequation (3.203), i.e.,
At this point, the reader should have a technical knowledge of the following aspects treated previously:
1) The conventional Dirac equation is not a two-body equation like the Schroedinger equation for the hydrogen atom, but represents one electron moving in vacuum under the external field of a proton. Consequently, the Dirac-Santilli isoequation represents the electron while being completely immersed within the hyperdense hadronic medium considered as external. Hence, the transition from the Dirac equation to the Dirac-Santilli isoequation is an effective way to reach a quantitative representation of the mutation of particles second only to the transition from the spinorial covering Lorentz-Poincare' symmetry to its isotopic covering outlined in Sections 3.10 and 3.11Q.
2) Santilli has strenuously opposed the idea that a particle in the core of a collapsing star has the same intrinsic characteristics (spin, charge, magnetic moment, etc.) as when nicely free in vacuum, as detected until now. Consequently, he has constructed relativistic hadronic mechanics for the quantitative studies of the biggest possible deviations of the intrinsic characteristics of particles when in vacuum. This is the general case of the Dirac-Santilli isoequation and its underlying Pauli-Santilli isomatrices reviewed in Section 3.11Q.
3) Since the proton is about 2,000 times heavier than the electron, the synthesis of the neutron can be well assumed as being a realization of the Dirac-Santilli isoequation without any mutation of the intrinsic characteristics. This feature was first well established by Santilli in his nonrelativistic analysis, and then adopted for the relativistic study as being valid to first order. Hence, the Pauli-Santilli isomatrices used in the neutron synthesis are indeed lifted, but they admit conventional eigenvalues for spin 1/2.
By using the above theoretical and experimental foundations previously established in vast studies (Chapters 1, 2, 3, 4, 5), Santilli relativistic, exact and invariant representation of all characteristics of the neutron in its synthesis from a proton and an electron is elementary and can be summarized as follows.
6.3F. Relativistic, exact and invariant representation of the neutron rest energy, meanlife and charge radius
Recall that the characteristic quantities of the spacetime isounit are not arbitrary parameters such as those used to adapt nature to a preferred theory (e.g., as it is the case for the chaoticity parameters to of the Bose-Einstein correlation), but represent actual, experimentally measured physical characteristics of hadrons.
In fact, the space characteristic quantities nk, k = 1, 2, 3, represent the actual dimension and shape of the neutron by characterizing its semiaxes normalized to the value 1 for the perfect spheridicity. Similarly, the forth characteristic quantity n4 represents the density of the neutron (defined as the ratio between the rest energy and the volume) normalized to the value 1 for the vacuum, as done for the index of refraction.
In his nonrelativistic 1990 paper, Santilli assumes the neutron is perfectly spherical and that the spin of the isoelectron is conventional. However, in the relativistic treatment of 1993, Santilli no longer assumes the neutron as being perfectly spherical, with consequential mutation of the spin, and assumes the numerical value of the neutron density n4 from the best data available at that time, the representation of the Bose-Einstein correlation via hadronic mechanics, Eqs. (5.69), i.e.,
A fundamental function of Santilli isorelativity is that of characterizing the isorenormalization of the rest energy, namely, the mutation of the conventional value of the rest energy of a particle when immersed within a hyperdense medium, according to Isoaxiom V (Section 3.10)
The use of the above experimental value of the neutron density then yields the representation of the rest energy of the isoelectron
from which Santilli obtains the exact and invariant representation of the rest energy of the neutron
with negative binding energy
while for conventional quantum mechanics the representation of the mass of the neutron would require the anathema of a "positive binding energy." It should be stressed that the above binding energy is entire of Coulomb origin due to the attraction between the proton and the isoelectron, since the strong hadronic forces are nonpotential and, consequently, they cannot characterize any binding energy.
Santilli also notes that value (5.69) represents the density of the proton-antiproton fireball in the Bose-Einstein correlation, which density is expected as being bigger than that of the neutron. Under the assumption of a null potential energy Santilli gets the limit values
that recovers the nonrelativistic result in first approximation
The relativistic, exact and invariant representation of the meanlife and charge radius was done in Santilli 1993 from the radial component of the Dirac-Santilli isoequation, thus being similar to the nonrelatvistic and and its review is omitted here for brevity.
6.3G. Relativistic, exact and invariant representation of the neutron spin.
Recall from Figure 6.11 that, under the assumption that the proton is un-mutated, the representation of the spin of the neutron requires that the total angular momentum of the isoelectron is null, namely, that its spin is identical in absolute value, yet opposite to the mutated angular momentum. In his 1993 paper, Santilli readily verified this condition via the use of the isotopies of the angular momentum studied in Section 3.11Q for which
with algebraic solution
Note not only the mutated values of the third components, but also those of the magnitudes of conventional angular momentum. Note also that the relationship between the mutated values of the third components and those for the magnitudes are not conventional, as apparently necessary for the constrained conditions of the electron trapped inside the proton. Note finally the exact and invariant character of the solution, since it is based on the isotopies of the rotational and spin symmetries achieved for the first time in Santilli 1993.
6.3H. Relativistic, exact and invariant representation of the anomalous magnetic moment of the neutron.
Recall from Section 3.11Q that the Dirac-Santilli isoequation characterizes the following isotopies of the magnetic and electric dipole moments,
The above laws provide a technical representation of the well known semiclassical property that the deformation of a charged and spinning sphere necessary implies an alteration of its magnetic moment. In particular, we have a decrease (increase) of the magnetic moment when we have a prolate (oblate) deformation or when we decrease (increase) the angular momentum.
Recall that the total magnetic moment of model of Figure 6.11 requires three contributions,
Recall also from the Dirac-Santilli isoequation studied in Section 3.11Q that the intrinsic magnetic moment of the isoelectron is mutated into the expression
where now both characteristic quantities n4 and n3 are known. In this way, Santilli reached the following relativistic, exact and invariant representation the intrinsic magnetic moment of the isoelectron
The desired representation of the anomalous magnetic moment of the neutron is then given by the following orbital magnetic moment of the isoelectron
Note the decrease of the intrinsic magnetic moment of the electron that is fully in line with the decrease of the third spin component from 1/2 to 1/21/2. Note also that the above values are different than the corresponding nonrelativistic expressions because in the latter treatment Santilli assumed in first approximation that the spin, and, consequently, the intrinsic magnetic moment of the electron are not mutated. At a relativistic level a mutation of both spin and magnetic moment does occur. Such a result could be predicted by the underlying symmetry, the Lorentz-Poincare'-Santilli isosymmetry, for which the mutation of one intrinsic characteristic of a particle generally implies that of all others.
6.3I. Santilli's etherino vs Fermi's neutrino.
As the attentive reader may have noted, the need for the emission in the neutron synthesis of a neutrino emerges nowhere at both the non relativistic and relativistic levels. This aspect is best clarified by Santilli's recollections released for this book:
As it is well known, the word "neutrino" is an Italian name proposed by Enrico Fermi to mean "little neutron." Being a physicist born and educated in Italy, Enrico Fermi was and remains my scientific star, particularly in view of my research on new clean nuclear energies.
However, with the passing of time, I grew more and more uneasy about the hypothesis of the emission of a neutrino in the neutron synthesis inside stars
Of course, I understood fully the need for the neutrino hypothesis, in whose absence we have violations of conservation laws noted also by Pauli. However, nature is not that simple as all of us dream and, as a physicist, I needed clean quantitative evidence establishing the existence of the neutrino independently from my unbounded respect for Pauli, Fermi and the other founders of our physical knowledge.
My first difficulties dealt with the identification of the energy needed to emit a neutrino in nuclear beta decays. The difficulty is representative of the dichotomy quantum vs hadronic mechanics. For quantum mechanics, nuclei are points, in which case the neutrino hypothesis is necessary to salvage conservation laws.
However, for the covering hadronic mechanics, nuclei are represented as they are in the physical reality, extended and actually very large bodies for particle standards. It is then easy to see that, following the beta decay, electrons remain attracted by nuclei due to their opposite charges and, consequently, the electron energy is a function of their direction of emission, being maximal for radial emissions and minimal for tangential emissions, resulting in the experimentally detected bell-shaped curve of the energy of the electron. The (rather primitive for today's knowledge) 20th century nuclear physics assumed that the variation of energy inherent in such a bell-shaped behavior was "evidence" of the emission of the neutrino. However, specific calculations based on extended nuclei and nuclei-electron attractions then left no energy at all for the very existence of the neutrino. I then started to have serious doubts on the existence of neutrinos as physical particles in our spacetime.
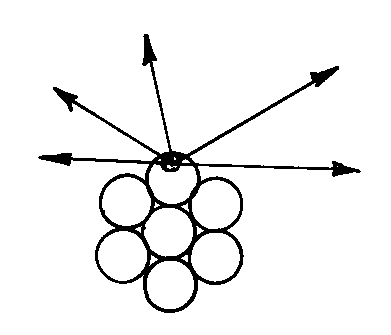
Figure 6.12. Reproduction of a drawing used by Santilli to illustrate that the variation of the kinetic energy in nuclear beta decay is due to the Coulomb interaction between the positively charged nuclei and the negatively charged electron, being maximal for radial emission and minimal for tangential emissions. This results in the well known bell-shaped behavior of the kinetic energy of the emitted electron with no energy at all to permit the very existence of the neutrino.
When I conducted in the 1980s systematic studies on the synthesis of the neutron from protons and electrons, my doubts on the existence of the neutrino grew considerably because I found the same dichotomy of quantum vs hadronic mechanics. In fact, Fermi had to assume the proton as being dimensionless because requested for the very consistency of quantum mechanics. Under such an assumption, the hypothesis of the neutrino is, again, necessary.
However, when studying the synthesis of the neutron with the covering hadronic mechanics, the situation is substantially different because, as soon as the extended character of the proton is admitted, the "orbital" angular momentum of the electron in its "compression" inside the proton is unavoidable. But the proton is hyperdense. Hence, the electron is constrained to orbit inside the proton along its spin, since other views would imply that the electron orbits inside the hyperdense proton against its spin, resulting in very implausible conditions.
Additionally, the proton and the electron can solely couple in singlet to prevent very strong repulsive forces of triplet coupling of extended particles one inside the other. I reached in this way in the mid 1980s the conclusion that the total angular momentum of the electron when immersed inside the proton is identically null because its spin is equal and opposite to its angular momentum. Consequently, the spin of the neutron coincides with that of the proton, without any possibility of identifying the neutrino anywhere.
As it is well known, half-odd-integer angular momenta are prohibited by the rotational symmetry SO(3) of quantum mechanics because they would violate unitarity, causality, and all that. However, the covering Lie-Santilli antisymmetry SO*(3) I had presented in my original 1978 memoir and studied subsequently in detail, readily admits half-odd-integer angular momenta in a fully invariant and causal way. As a matter of fact, the angular momentum in hadronic mechanics may have "continuously varying values" to prevent the theology that an electron in the core of a star can have the same discrete orbits as when isolated in vacuum.
More technically, in the transition from quantum to hadronic mechanics, Planck's constant h is replaced by the integral-differential isounit I*(t, r, p, ψ, ...) which becomes the basic unit of the Lie-Santilli isosymmetry SO*(3). Continuously varying, fully invariant and causal angular momenta are then a consequence of the locally varying character of the isounit. Invariance is guarantee by the fact that the unit is the basic invariant of any theory.
Following the achievement of the above technical knowledge, I was ready in the late 1980s to release for publication my first paper on the nonrelativistic representation of all characteristics of the neutron, thus including its spin, as a hadronic bound stated of a mutated proton and a mutated electron. A big dilemma soon emerged in writing the paper, whether I should disclose or not my view on the apparent lack of existence of the neutrino.
Since at that time I was dreaming of publishing such an innovative paper in a refereed journal, I decided to keep silence on the issue of the neutrino, with the intent of disclosing my doubts later on. Rutherford had published his conception of the neutron in the Proceedings of the Royal Society, Vol. 97, 1920, page 374 on. It is customary in physics to publish further advances in the journal of the origination of the idea. Hence, I submitted in 1988 my paper to the British Proc. Roy. Soc. in respect of Rutherford's memory because, after all, Rutherford had conceived the neutron as a bound state of a proton and an electron, to be later on dismissed by Pauli and others because impossible for quantum mechanics.
I still remember the months and months of fights with the editorial board of the Proc. Roy. Soc. to no avail. I was praying them to consider the paper in Rutherford's honor, I brought to their attention the potentially large societal implications for new clean energy, I appealed to scientific democracy for qualified inquiries because, after all, I had indeed proved the plausibility of Rutherford's original conception of the neutron as a bound state of a proton and an electron, all this to no avail. Rutherford's conception of the neutron required a necessary nonunitary generalization of quantum mechanics into hadronic mechanics and this occurrence caused clear hysteria in the editorial board of the Proc. Roy. Soc. to such a level to be offensive toward the memory of one of their most illustrious compatriots.
Still dreaming of publishing the paper in a conventional journal, I then submitted it to the journals of the Italian, American and other societies without disclosing my doubts on the existence of the neutrino, thus by using Fermi's reaction (6.149). The rejections used such strong language due to the surpassing of quantum mechanics to qualify as delicate in comparison the rejections by the Proc. Roy. Soc. To avoid that decades of research were wasted, I then published the paper in 1990 in the Hadronic Journal,
Apparent consistency of Rutherford's hypothesis on the
neutron as a compressed hydrogen atom
R. M. Santilli,
Hadronic J. Vol. 13, 513-531 (1990)
I was so discouraged by the absence of scientific contents of all these reviews that, as one can verify, I published the paper in the latest available form, that without any mention of the neutrino problem, thus with a clear inconsistency between the use of Eq. (6.149) showing a neutrino and Figure 6.11 of the paper showing lack of its need.
Despite these academic shortcomings, my uneasiness with the neutrino hypothesis grew deeper the deeper I studied the issue. I noted that, indeed, the Lorentz-Poincare' (LP) symmetry does require the "independent" conservation of the total linear and total angular momenta. However, such a symmetry solely holds for Keplerian systems, that is, for isolated masses moving in vacuum without contact or collisions all around a heavier Keplerian nucleus. I could not possibly accept the validity of the Lorentz-Poincare' symmetry for the structure of the neutron, I never did and never will, because the structure of the neutron does not admit a Keplerian center.
Hence I spent decades for the construction of covering symmetry specifically conceived for non-Keplerian systems such as the neutron, today known as the Lorentz-Poincare'-Santilli (LPS) isosymmetry. It was then easy to see rather radical changes in the transition from the LP to the LPS symmetry. In fact, the LP symmetry requires isolated point-masses particles moving in empty space without contact or collisions. By comparison, the LPS symmetry was conceived for particles totally immersed one inside the other, thus including inevitable constraints.
The technical characterization of the neutron constituents as (iso)-unitary irreducible (iso)-representations of the LPS symmetry, the isoprotons and the isoelectrons, confirms fully the lack of any need for the neutrino hypothesis to such an extent that its presence caused catastrophic inconsistencies. To begin, for an isolated neutron, the conservation of the linear and angular momenta of its constituents has no physical meaning, the sole conservation law being that of the total energy and the uniform motion of the center of mass.
Additionally, that constrained systems admit the transformation of linear into angular momenta and viceversa, as it is typically the case of a "sling shot", each physical quantity represented in the conservation of the total energy. Consequently, in the neutron synthesis, constrains cause the transformation of linear into angular momenta without any need to emit a neutrino for both the neutron synthesis and its spontaneous decay.
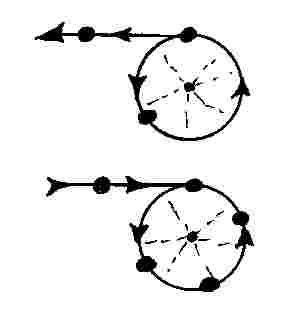
Figure 6.13. Reproduction of the original drawing made and used by Santilli to illustrate the absence of a neutrino in both the neutron synthesis and its decay. In the neutron synthesis in the core of a star (bottom view) the linear momentum of the electron is constrained to be turned into its angular momentum when compressed inside the proton. In the spontaneous decay of the neutron, we have the opposite event in which the constrained angular momentum is transformed into the linear momentum of the expelled electron, its spin being not mutated in first nonrelativistic approximation in both cases.
Despite these personal convictions, I published all additional relativistically and relativistic papers on the structure of the neutron in 1992, 1993 and 1995 by using Fermi's hypothesis on the neutrino without any mention of my doubts on its existence. This was due in part to my reverence for Enrico Fermi but also to my long experience that novelty in academia is the enemy to destroy at whatever cost. Since the neutrino hypothesis was deeply rooted in all segments of the physics of the time, from prep courses to large grants for very costly "neutrino detectors," I elected to keep my doubts to myself, yet my papers based on reaction (6.149) were structurally inconsistent because of the redundancy of spin 1/2, something no reviewer noted.
Yet, my uneasiness on the neutrino hypothesis kept growing in time and so did the disparity between my views and the so-called "mainstream neutrino physics." On theoretical grounds, Fermi's original conception of one massless and chargeless neutrino and one antineutrino was first enlarged to three different neutrinos (the electron, muon and tau neutrinos) and three antineutrinos although without any clear structural, experimentally measurable distinction, since flavor and other SU(3) features cannot be defined in our spacetime.
This enlargement turned out as being insufficient "to fix things," namely, to achieve compatibility with the standard model. Hence, the three neutrinos and three antineutrinos were assumed to have "masses" used for fitting data. This broadening of Fermi's original conception was and remains unacceptable to me because I already had difficulty in accepting that a massless particle could traverse entire planets and stars, that is, pass through the hyperdense media of something like 1010 nuclei without collision. But then, I could not possibly accept and never will accept as plausible idea that massive neutrino can pass through 10100 superdense nuclei without appreciable collision.
Then the hypothesis of three different massive neutrinos and three different massive antineutrino turned out as being still insufficient for achieving compatibility with the standard model. Hence, the so-called "main stream neutrino community" ventured the additional conjecture, immediately accepted by journals of all physical society around the world because proffered by high ranking physicists, that "neutrino oscillates" (loosely speaking different neutrinos can transform into each other).
My increasing uneasiness was due to the fact that one experimentally unverifiable but insufficient conjecture was being replaced with a broader equally unverifiable conjecture to fix the preceding one. When the new conjecture turned out as being insufficient, a yet broader, equally unverifiable conjecture was voiced. Consequently, I asked myself the question: when will this chain of unverifiable conjectures stop? Clearly the field requires a profound structural revision to regain plausibility since the maintaining of the theoretical status quo is no longer tenable.
On experimental grounds, my uneasiness on neutrino conjectures was even greater than that for theoretical profiles. Fermi had clearly stated that "neutrinos cannot be directly detected," evidently because they were assumed as being massless and chargeless. I still remember the first serious effort at the detection of neutrinos done in the 1980s in Italy with the construction of the "Gran Sasso Laboratory," consisting of a very large chamber excavated under the Gran Sasso Mountain in the Central Apennines, that was filled up with distilled water and equipped with various detectors. The laboratory was set up for the intent of detecting hypothetical events caused by neutrinos coming from the opposite side of Earth, while the Gran Sasso mountain was intended as a shield for cosmic rays and other radiation. Following five years of measurements, the laboratory produced no measured event worth considering.
Rather than initiating a serious re-inspection pf the foundations of the neutrino conjectures, the "mainstream neutrino community" immediately reacted in the late 1980s with the granting of Nobel prizes for the "discovery of neutrinos" after which any physicist claiming of their lack of existence was in need of psychiatric assistance for the establishment. "Experimental neutrino physicists" also moved to the attack of canceling the debacle caused by the Gran Sasso Laboratory with the design of bigger and bigger "neutrino detectors" that, as such, required bigger and bigger public funds.
Evidently, I always accepted the data originating from these "neutrino experiments" as real. That's not the issue. The issue is the "interpretation" of these data via neutrino conjectures since alternative interpretations are indeed possible, and one among others will be indicated shortly. I could not possibly accept these interpretations because of:
1) The extremely few events in "neutrino detections" over an extremely large number of events, thus having statistics insufficient for a final experimental claim.
2) The new "neutrino detectors" often contain radioactive isotopes whose decay could itself cause the very few events assumed as being "evidence of neutrinos," while being in reality events prohibited by quantum mechanics yet fully permitted by the covering hadronic mechanics, such as certain stimulated double beta decays.
3) The elaboration of the data was based on the assumption of the exact validity of the LP symmetry under conditions it was expected as being inapplicable, as it was eventually verified.
The main issue is that, on strict scientific grounds, all the past and ongoing neutrino experiments are indeed valuable, but they cannot claim direct detection of neutrinos, as stated by Fermi. These experiments essentially identify physical particles in our spacetime whose production is merely conjectured as being due to neutrinos. Once the indirect character of the detection is admitted, one can see the possibility of alternative interpretation of exactly the same experimental data with new theories without the litany of problems of neutrino conjectures, a process that is indeed under way at this writing (summer 2010).
My uneasiness on neutrino conjectures reached uncontrollable levels when I started to apply the preceding results to astrophysics, with particular reference to the study of the synthesis inside stars of light , natural, and stable element. As it is well known, the synthesis of the neutron requires 0.782 MeV (for which value there is no energy at all for the neutrino). The evident question was: where is this energy coming from?
As well known, a star initiates its life as large aggregates of hydrogen, first synthesizes neutrons from hydrogen atoms, and then synthesizes the deuterium, the helium and all other natural isotopes. The important point is that the first synthesis of neutrons "requires" energy, energy being "released" only in the subsequent nuclear syntheses.
It was easy to see that the missing 0.782 MeV per neutron cannot originate from the star itself. In fact, at the majestic initiation of its life, even a small star can synthesize 1050 neutrons per seconds. In the event the missing 0.782 MeV per neutron originated from the star interior, the star could not possibly initiate emitting light because it would "lose" 1050 MeV per seconds and produce no light.
These and other astrophysical considerations confirmed all my uneasiness on neutrino conjectures because I was clearly facing with the need for a structurally new approach to the neutron synthesis. In 2005 I received the visit at IBR in Florida of a distinguished, high ranking colleague (whose name I cannot disclose to prevent that his academic and personal lives be disrupted by neutrino fanatics). Since we knew and respected each other for decades, I decided to download on him all my doubts on neutrino conjectures. To my surprise, he shared them all and indicated that he too had elected to be silent to prevent hysterical reactions by neutrino fanatics. He also indicated that numerous other important physicists (whose names I also cannot disclose) had serious doubt on the neutrino business, a rather widespread condition among serious physicists.
That was it! The awareness that I was far from being alone for my doubts on neutrino conjectures gave me strength to publish my ideas. I plunged myself in the writing of the first paper on the neutron synthesis without neutrino, I presented the content at the 2006 meeting of the "International Association of Relativistic Dynamics" (IARD) held at the University of Connecticut in Storrs, I saw the plausibility of the ideas in the eyes and comments of the audience, and published in 2007 the paper
The etherino and/or the neutrino hypothesis
R. M. Santilli,
Foundation of Physics, Vol. 37, 670 (2007)
The main content is that, since the missing energy cannot plausibly originate from the star itself, it originates from space conceived as a universal medium of very high density (the historical ether) necessary not only for the existence and propagation of electromagnetic waves (no 'wave" can possibly exist without a "medium"!) but also for the existence and propagation of truly elementary particles such as the electron and, therefore, of all matter at large. I then introduced s new entity under the name "etherino with symbol "a" (from the Latin "aether") and proposed the following alternative to reaction (6.149)
with the isodual expression for the antineutron
To prevent the already large zoo of unknown particles, I stressed in the 2007 paper that the etherino was "not" proposed as being a particle. but was merely intended to represent the transfer of energy and other quantities from the ether to the neutron. I also indicated the new meaning of hadronic mechanics as permitting a quantitative study of the ether as a universal substratum with high energy density and its interaction with visible matter. In fact, the etherino cannot even be conceived with conventional, quantum Hilbert spaces over conventional fields, and necessarily require the covering Hilbert-Santilli isospaces over isofields.
Contrary to superficial impressions without prior technical knowledge, the connection between Fermi's neutrino and Santilli's etherino is quite deep. In fact, the synthesis of the neutron requires a third entity in the left-hand-side, according to Fermi's hypothesis (6.149)
Comparison of reactions (6.150) and (6.152) shows that they may eventually result as being the same. However, the "interpretation" changes dramatically. Fermi's neutrino is assumed as being a physical particle in our spacetime with consequential great uneasiness at the idea that neutrinos could traverse something like 10100 hyperdense nuclei without appreciable collisions.
By contrast, Santilli's etherino is an impulse propagating through the ether that, as such, can indeed cross 10100 hyperdense nuclei because the propagation is in the underlying medium and not through matter. In short, I conceived the etherino to remove the biggest implausibility of neutrino conjectures, while preserving experimental data as indicated below.
It has to be of "longitudinal" character (potentially it would be an ordinary electromagnetic wave), thus resolving the uneasiness of traversing entire planets and stars without collisions because the propagation occurs in the underlying universal medium.
Subsequently, I initiated astrophysical studies still under way to discover a number of events that appear to require more energy than that contained in stars, thus requiring the acquisition of energy from the ether. One of them is the supernova explosion generally occurring at the end of life of a star. It is evident that the star still remains as a large reservoir of fusion energy. However, calculations show that such a reservoir is grossly insufficient to explain the immensity of the energy in the explosion of a supernova that remains visible to the naked eye at billions of light years distances. The only numerical explanation I could come out in this case is that supernovas somehow trigger the transfer of immense energies from the ether to our visible world.
Additionally, these astrophysical studies brought again to my attention the old, fascinating theories of the "continuous creation" in the universe. It was then immediate to see that the etherino is essentially an alternative formulation of continuous creation, since it carries energy from the ether, thus energy that did not previously exist in our physical world. By studying deeper and deeper these astrophysical aspects, I became convinced that all stars are indeed a source of continuous creation in the sense that they have mechanisms for extracting energy from the ether.
Electromagnetic waves are known to be traverse. Hence, the neutrino could not be characterized by an equally transverse oscillation of the ether otherwise it would be an ordinary photon with a host of sequential inconsistencies in reaction (6.150). This and other aspects suggested that the etherino is expected as being a "longitudinal" impulse propagating through th ether. It is then possible to see that exactly the same experimental data on "neutrino detections," as available, can be identically re-elaborated via the etherino hypothesis.
Far from being a mere scientific curiosity, the implications are very intriguing indeed. In fact, currently available experimental data on neutrino events could be the type of a big scientific iceberg yet to uncover, the discovery of a new form of communication through space that, being longitudinal, is expected as being millions of times faster than the speed of electromagnetic waves. Hence, future generations of scientists have the possibility of establishing a new form of very rapid interstellar communication for which electromagnetic waves are similar to the smoke signals used by American Indians.
In closing, a most rewarding personal aspect is that, after such a long scientific journey that required new mathematics, new physics, new experiments and all that, I was forced to go back to the first paper I wrote when still a high school student and published during my first year of physics courses,
Perche' lo spazio e' rigido (Why space is rigid)
R. M. Santilli, Il Pungolo verde, Campobasso, Italy, (1956)
were I presented the conception of the ether as a universal medium of great rigidity (because electromagnetic waves are traverse) and the elimination of the "ethereal wind" used at the time to deny its existence. The latter was achieved by noting that the electron is a "pure oscillation" with the frequency of 0.829 x 1020 Hz, that is, an oscillation without a "little mass" oscillates in its interior. Consequently, the oscillation can only be realized by a point of the ether. When an electron is moved, its characteristic oscillation is moved from a region of the ether to another, and no "ethereal wind" is conceivably possible. The paper then extrapolated this basis features to matter at large. Inertia was conceived as the resistance by the ether against accelerations. Already at my first year undergraduate course of physics I dismissed any intrinsic value to mass, and considered its energy equivalent as the really basic characteristics.
According to this view, the universal substratum is necessary for the very existence as well as of propagation of all visible entities, including electromagnetic waves, elementary particle and matter at large, because waves, oscillations, strings and all that cannot plausibly exist without a medium.
In short the 2007 paper the confirmed my 1956 paper on the ether as a truly universal substratum to the effect that, contrary to our sensory perception, matter is totally "empty" in the sense that there is no "little solid" oscillating in the structure of the electron and other elementary particles, and space is totally "full" in the sense that it is a universal medium of extremely high density filling up the entire universe with no voids nowhere.
6.3J. Structure model of the remaining baryons with physical constituents
Santilli extended the results of his structure model of the neutron to the octet of baryons in the 1997 memoir
Relativistic hadronic mechanics: nonunitary, axiom-preserving
completion of relativistic quantum mechanics
R. M. Santilli,
Found. Phys. Vol. 27, 625-729 (1997)
resulting on hadronic structure model of the type here presented with increasing mass, and, therefore, increasing number of elementary constituents as per rules of Section 6.1C:
etc. It is an instructive exercise for the interested reader to prove that the hadronic structure model of the preceding sections permits an exact and invariant representation of all characteristics of the particle considered. It is equally instructive to prove that in each case we have the suppression of the atomic spectrum of energy down to one energy level only, that of the particles considered via the characteristic solution k1 of increasing (positive) values bigger than 1 and k2 more and more closer, but bigger than 1, as in values (6.62), thus ensuring the suppression of the atomic spectrum down to only one level.
In continuing the model to heavier baryons a number of additional rather complex events occur, such as pair creation inside hadrons. Quantitative studies of these events require the prior development of hadronic field theory that has not been constructed to date. As such, these aspects are deferred to the specialized technical literature.
6.3K. Compatibility of baryon syntheses with the SU(3) classification.
The compatibility of the syntheses of baryons with SU(3) classifications was achieved in the 1997 memoir in a way similar to that for mesons, Eq. (6.92), namely, with the following total isounit for the octet of barions
and then the construction of the hypersymmetry SU*(3) characterized by the above hyperunit (see Chapter 2 and quoted literature and Section 4.5). The isomorphism between such a hypersymmetry and the conventional SU(3) symmetry confirms the achievement of the desired equivalence under new intriguing degrees of freedom that can be used to resolve at least some of the remaining problems, such as the spin of baryons.
6.4. LABORATORY SYNTHESIS OF NEUTRONS FROM A HYDROGEN GAS
6.4A. Introduction
The laboratory synthesis of neutrons from a hydrogen gas according to Rutherford's conception is, by far, one of the most basic and important experiments of contemporary physics, with epistemological, scientific and environmental implications mostly beyond our comprehension at this time, hence, the need for its resolution one way or the other.
In fact, as stressed by Santilli in his works, the neutron is one of the biggest reservoirs of clean energy available to mankind since it decays spontaneously (when isolated) by emitting a highly energetic electron whose easy capture via a metal shield would produce a clean source of heat and electricity. Consequently, as we shall see in the next chapter, the neutron may admit mechanisms for its stimulated decay, with vast environmental implications. However, as stressed by Santilli in his works, the laboratory synthesis of the neutron outlined in this section is an evident pre-requisite for its possible stimulated decay outlined in the next chapter.
Additionally, as also stressed by Santilli, the neutron synthesis is the first and most fundamental fusion occurring in stars, since fusions synthesizing natural isotopes can only occur following the neutron synthesis. Therefore, no study of nuclear fusions can be truly exhaustive, or sufficiently deep, without prior experimental knowledge on the neutron synthesis.
Despite the above diversified fundamental relevance, the laboratory synthesis of neutrons from a hydrogen gas is incompatible with quantum mechanics. Consequently, the neutron synthesis has been generally opposed by academia for about half a century because its confirmation would terminate the current, widespread, preferred dominance by quantum mechanics for all conditions existing in the universe in favor of the covering hadronic mechanics.
The laboratory synthesis of the neutron from a hydrogen gas was first reached in the 1960s by the Italian priest-physicist of the University of Milan, Don Carlo Borghi and his colleagues, Don Carlo Giori and Antonio Dall'Olio. Being Italians, the experimentalists attempted to conduct first the test in Italy, but encountered extreme difficulties and were forced to conduct the experiment at the CEN Laboratories in Recife, Brazil. The results were presented in the following communications
C. Borghi, C. Giori C. and A. Dall'Olio, Communications of CENUFPE, Number 8 (1969) and 25 (1971),
whose publication was rejected by various journals on grounds that the synthesis is not possible because contrary to quantum mechanics. Don Borghi continued to try for the rest of his days to dismiss his findings with independent re-runs, since experiments can solely be dismissed via counter-experiments and not via theoretical theologies, with no avail. No laboratory of his time could even consider the re-run of the test despite its evident fundamental character. Subsequently, Santilli managed to have one of the papers published in Russia as part of the proceedings
C. Borghi, C. Giori C. and A. Dall'Olio, (Russian) Phys. Atomic Nuclei, Vol. 56, 205 (1993).
The test is today known as Don Borghi's experiment. The above references will be quoted in this section as Don Borghi 1969 and 1993.

Figure 6.15. A view of Don Carlo Borghi in the 1960s
Due to its fundamental character, Santilli proposed for some thirty years the repetition of Dom Borghi's experiment to numerous nuclear physics laboratories around the world to receive flat rejections at best. With the passing of the years, Santilli and his associates constructed hadronic mechanics and achieved the exact representation of all characteristic of the neutron in its synthesis from the hydrogen atom as reported in Section 6.3. Hence, the laboratory verification of the neutron synthesis became more and more necessary with the passing of time since the dismissals of the experiment via quantum mechanical arguments were no longer scientific.
After realizing the impossibility of testing the neutron synthesis in academic laboratories, Santilli had no other choice than that of doing the test himself at the laboratory of the Institute for Basic Research in Tarpon Springs, Florida, with the assistance of the IBR technicians J. Judy, G. West, M. Rodriguez, J. Alban and R. Jones.
The tests were conducted and repeated throughout the entire 1996 and concluded in early 1997 by confirming in full Don Borghi's results, although with a number of variations in its technical realization. The combined tests are today known as the Don-Borghi-Santilli experiment.
The paper presenting the measurements was rejected by journals of various physical societies on the same dismissals received by Don Borghi some forty years earlier, namely, that the claimed measurements are impossible because prohibited by quantum mechanics without any consideration of the complete solution then available via the covering hadronic mechanics. Santilli then published the paper in the Hadronic Journal
"Apparent confirmation of Don Borghi's experiment toward the synthesis of neutron from protons and electrons"
R. M. Santilli, Hadronic Journal Vol. 30, 709 (1997).
with the identification of the primary rejections in the main page. Santilli also provided the following website for detailed listing of scans and data
"The synthesis of the neutron according to hadronic mechanics"
R. M. Santilli, website (1997).
Fiugure 6.16. A photo of Ruggero Maria Santilli by the Club Med, Martinique, April 2008.
This section is mainly derived from Kadeisvili's 2008 review
The Rutherford-Santilli neutron
J. V. Kadeisvili,
Hadronic J. Vol. 31, 1-114 (2008)
6.4B. Don Borghi experiment on the synthesis of neutrons from an hydrogen gas
Don Borghi's 1969 experiment is truly simple and of easy duplication with very low costs. In essence, the experimentalists placed in the interior of a cylindrical metal chamber (called klystron) a hydrogen gas at a fraction of 1 bar pressure and kept partially ionized via an electric arc with about 500 V and 10 mA. Additionally, the gas was traversed by microwaves with 10-10 s frequency. Since protons and electrons are charged, they could not escape from the metal chamber, and remained trapped in its interior.
In the cylindrical exterior of the chamber, the experimentalists placed various materials suitable to be activated when exposed to a neutron flux (such as gold, silver and other substances). Following exposures of the order of days or weeks, the experimentalists reported nuclear transmutations due to a neutron count of up to 104 cps, apparently confirmed by β emissions evidently not present in the original material.
Figure 6.17. A view of Don Borghi's test equipment on the left and a typical activation curve on the right.
Note that Don Borghi's experiment makes no claim of direct detection of neutrons, and only claims the detection of clear nuclear transmutations that can only be caused by a neutron flux. Note also the dual presence of the electric arc plus the microwave. Note finally the credibility of the source, two of the experimentalists (Don Carlo Borghi and Don Camillo Giori) being Catholic priests.
Needless to say, Don Borghi experiment is in need of numerous independent reruns, either in its original form, or in one of several alternatives discussed in the next section. Nevertheless, Don Borghi experiment constitutes the first historical test on Rutherford's conception of the neutron, and it is remarkable, not only because of the claimed results, but also because of its simplicity and low cost, yet fundamental scientific implications.
Figure 6.18. A view of Don Borghi's activation data.
6.4C. Santilli experiment on the synthesis of neutrons from a hydrogen gas
Santilli experiment reported in the 2007 paper consists of a cylindrical chamber (the klystron) filled up with a hydrogen gas and solely traverses by an electric arc without any microwave. The chamber was constructed via transparent PVC so as to assure via visual inspection the activation of the arc. This experimental set up was selected for the specific purpose experiment. The expectation was that, in the absence of any detection of a neutron flux via the sole use of the electric arc, the addition of high frequency microwaves was expected to be necessary.

Figure 6.19.A view of Santilli's simple experimental set up showing the Miller DC Welder on the right, the PVC klystron in the center and the hydrogen pressure bottle on the left.
With reference to the website for pictures and further data
"The synthesis of the neutron according to hadronic mechanics"
R. M. Santilli, website (1997).
Santilli conducted the radiation counts via:
1) A detector model PM1703GN manufactured by Polimaster, Inc., with sonic and vibration alarms as well as memory for printouts, with the photon channel activated by CsI and the neutron channel activated by LiI. For reasons still under investigation (see below), the Li-activated neutron detectors resulted to be the most active and its use is necessary for any serious repetition of Santilli's tests.
2) A photon-neutron detector SAM 935 manufactured by Berkeley Nucleonics, Inc., with the photon channel activated by NaI and the neutron channel activated by He-3 also equipped with sonic alarm and memory for printouts of all counts. This detector was used to verify the counts from the preceding one.
3) A BF3 activated neutron detector model 12-4 manufactured by Ludlum Measurements, Inc., without counts memory for printouts. This detector was used to verify the counts by the preceding two detectors.
Electric arcs were powered by welders manufactured by Miller Electric, Inc., including a Syncrowave 300, a Dynasty 200, and a Dynasty 700 capable of delivering an arc in DC or AC mode, the latter having frequencies variable from 20 to 400 Hz.

Figure 6.20. One our of the large number of print-outs from the Berkeley Nucleonics detector Sam 935 following a neutron alarm in Santilli's 2007 tests.
The following three different klystrons were manufactured, tested and used for the measurements (see the website for pictures):
Klystron I: A sealed cylindrical klystron of about 6" outside diameter (OD) and 12" height made of commercially available, transparent, PolyVinyl Chloride (PVC) housing along its symmetry axis a pair of tungsten electrodes of 0.250" OD and 1" length fastened to the tip of 0.250" OD copper rods protruding through seals out of the top and bottom of the klystron for electrical connections. The electrodes gap was controllable by sliding the top conducting rod through the seal of the flange.
The klystron cylindrical wall was selected to be transparent so as to allow a visual detection of the arc because, as shown below, in the absence of a true DC arc within a pure hydrogen gas, no detection is possible.
Following initiation of a real DC arc within the hydrogen filled klystron, there were hours and at times days of no detection at all by all counters. However, hours after shaking the klystron, detections occurred in a systematic and repetitive way.
The detection were triggered by a neutron-type particle, excluding contributions from photons (because often their count were null as shown by the scans), and they were definitely not due to vibrations. However, these detections were anomalous, that is, they did not appear to be due to a flux of actual neutrons originating from the klystron.
This anomaly is established by the repeated "delayed detections," that is, exposure of the detector to the klystron with no counts of any type, moving the detector away from the klystron (at times for miles), then seeing the detectors enter into off-scale vibrational and sonic alarms with zero photon counts.
The first case of this type occurred when Prof. Santilli exposed detector PM1703GN to the klystron following the arc, put the detector in his briefcase and went to a local Walgreen store for purchases, which store is located some 15 m driving distance from the lab. To Prof. Santilli's great surprise and embarrassment, the detector in his briefcase entered into a maximal off-scale, sonic and vibrational, neutron alarm while he was in line for the payment of his bill. He had to leave his purchases and rush out of the store while the store personnel was calling security for control.
The 15 m "delayed self-activation" was reproducible with detector PM1703GN with the same time delay but in different locations although not with the other two who showed a different type of anomalous count (see [24] for brevity), thus establishing a dependence of the neutron counts from the type of activation as well as on the casing material of the detector itself.
Klystron II: A rectangular, transparent, PVC klystron 3" x 3" x 6" filled up with commercial grade hydrogen at atmospheric pressure and temperature traversed by a 2" long electric arc powered by a standard Whimshurst electrostatic generator.
This klystron was conceived for an implosion caused by combustion with atmospheric oxygen, thus explaining the small size of the klystron. This test was conducted only once because of instantaneous off-scale detection of neutrons by all detectors such to cause evacuation of the laboratory. Hence, this test was not repeated for safety.

Figure 6.21 One out of a number of print-outs from the Polimaster detector PM1703GN following one of the sonic and vibrational alarms that caused evacuation of the laboratory in Santilli's tests.
Klystron III: A cylindrical metal klystron fabricated in schedule 80 carbon steel pipe with 12" OD, 0.5" wall thickness, 24" length and 3" thick end flanges capable of withstanding hydrogen pressure up to 500 psi with the internal arc between thoriated tungsten electrodes controlled by outside mechanisms.
This test was conceived for the conduction of the test at bigger hydrogen pressure compared to that of Klystron I. The test was conducted only once at 300 psi hydrogen pressure because of instantaneous, off-scale, neutron detections such to cause another evacuation of the laboratory.
It should be stressed that Santilli had no intention or interest in measuring the cps, since that would have been premature and, in any case, required much more sophisticated equipment. Hence, the main purpose of Santilli's tests was to establish the production of neutron-type particles via a DC arc within a hydrogen gas.
No meaningful counts were detected with the above identified klystrons in using various gases other than hydrogen, although this should not exclude possible similar effects under sufficiently more powerful arcs. No neutron, photon or other radiation was measured from electric arcs submerged within liquids. Hence, the data herein reported appear to be specific for electric arcs within a hydrogen gas under the indicated conditions.
At the end of the tests, all detectors were returned to their manufacturers for control, and all detectors were certified as operating properly. The manufacturers then released the scans accumulated in the detector memories, some of which are reproduced in web site [42].
In summary, Santilli states in his 2007 paper that an electric arc within a hydrogen gas at a few psi pressure and atmospheric temperature as above described for Klystron I produces "entities" that:
1) Are not hydrogen atoms (because in that case no nuclear transmutation would be conceivably possible);
2) Have dimensions of the order of 1 fm as for all hadrons (otherwise the detectors would show no counts);
3) Are neutral (otherwise they would not move through walls);
4) Are stable for hadron standards (more accurate data being grossly premature at this writing);
5) Remain initially confined within the arc chamber under steady conditions, to slowly exit, except for the case of production under implosion causing rapid propagation;
6) Are generally released hours following the tests, with anomalous counts lasting for weeks;
7) Are not neutrons due to the anomalous behavior of the detectors.
Santilli does not exclude that the "entities" produced in the tests with Klystrons II and III are indeed actual neutrons, due to the instantaneous as well as off-scale nature of the neutron alarms in clear absence of photon or vibrations.
Whatever their interpretation, we can state that Santilli's 2007 experiment confirms Don Borghi's 1969 experiment because the latter test detected nuclear transmutations on various substances placed in the outside of the klystrons, which transmutations are necessary under the detected neutral particles in Santilli's tests.
6.4D. The Don Borghi-Santilli neutroids
Santilli excludes that the entities produced in the tests with Klystron I are true neutrons for various reasons, such as:
1) The anomalous behavior of the detectors, for the case of the 15 m delay, self-activated detection indicates first the absorption of "entities" producing nuclear transmutations that, in turn release ordinary neutrons.
2) Stars can indeed produce the missing energy of 0.78 MeV for the neutron synthesis, but the environment inside Klystron I is not expected do the same, due to the very low density of the hydrogen gas, the low power of the DC welder and other factors.
3) The physical laws of hadronic mechanics do not allow the systematic synthesis of the neutron under the conditions of Klystron I because of the need of the trigger, namely (see Sections 6.2 and 6.3), an external action bringing the proton and the electron at 10-13 cm mutual distances, that is, permitting the transition from quantum to hadronic conditions. In fact, the tests with Klystrons II and III do admit such a trigger and have apparently produced neutrons.
In view of these and other reasons, Don Borghi submitted in his 1969 paper the hypothesis that the "entities" are neutron-type particles he called neutroids. Santilli adopted this hypothesis and presented the first technical characterization of neutroids with the symbol ñ and the characteristics in conventional; nuclear units A = 1, Z = 0, J = 0, amu = 0.008. Hence, Santilli assumed that in Klystron I he produced the following reaction precisely along Rutherford's original conception
where: the value J = 0 avoids the spin anomaly in the neutron synthesis as indicated in Section 3; the rest energy of the neutroids is assumed as being that of the hydrogen atom because in atomic mass units
for which the hydrogen mass is given approximately by 1.008 amu; the p-e binding energy of Coulomb nature is too small for the approximation considered, being of the order of 10-3 MeV.
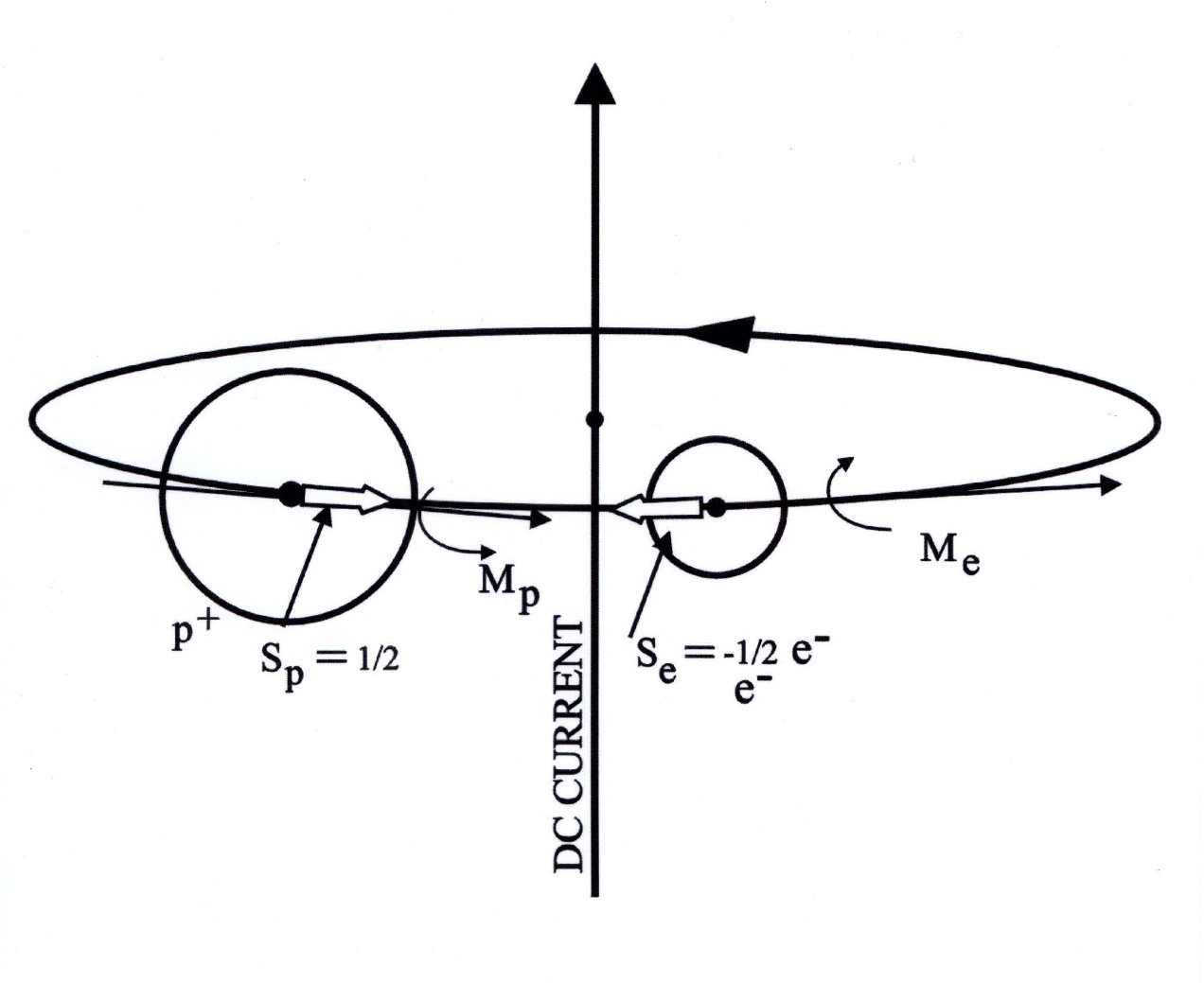
The interpretation submitted by Santilli is that the geometry of the electric arc is quite conducive to processes causing the synthesis of neutron-type particles. By recalling that the magnetic field created by an electric arc is directly proportional to the current and inversely proportional to the distance, in the conditions of Santilli's tests, protons and electrons are exposed to magnetic field with an intensity of the order of 109 Gauss when at atomic distances from the arc.
Under so powerful a magnetic field, the geometry of the electric arc first aligns protons and electrons with opposite polarities of their magnetic moments along the tangent to the local magnetic force. Subsequently, the same geometry is predicted to cause protons and electrons to collapse into a neutral, hadron-size particle due to the very strong Coulomb attractions at short distances of both, opposite charges and opposite magnetic polarities (see the figure).
The creation of neutroids is then due to additional reasons, such as the tendency of DC electric arc of compressing magnetically polarized particles toward the arc itself, resulting in the creation of the neutron-type neutroids.
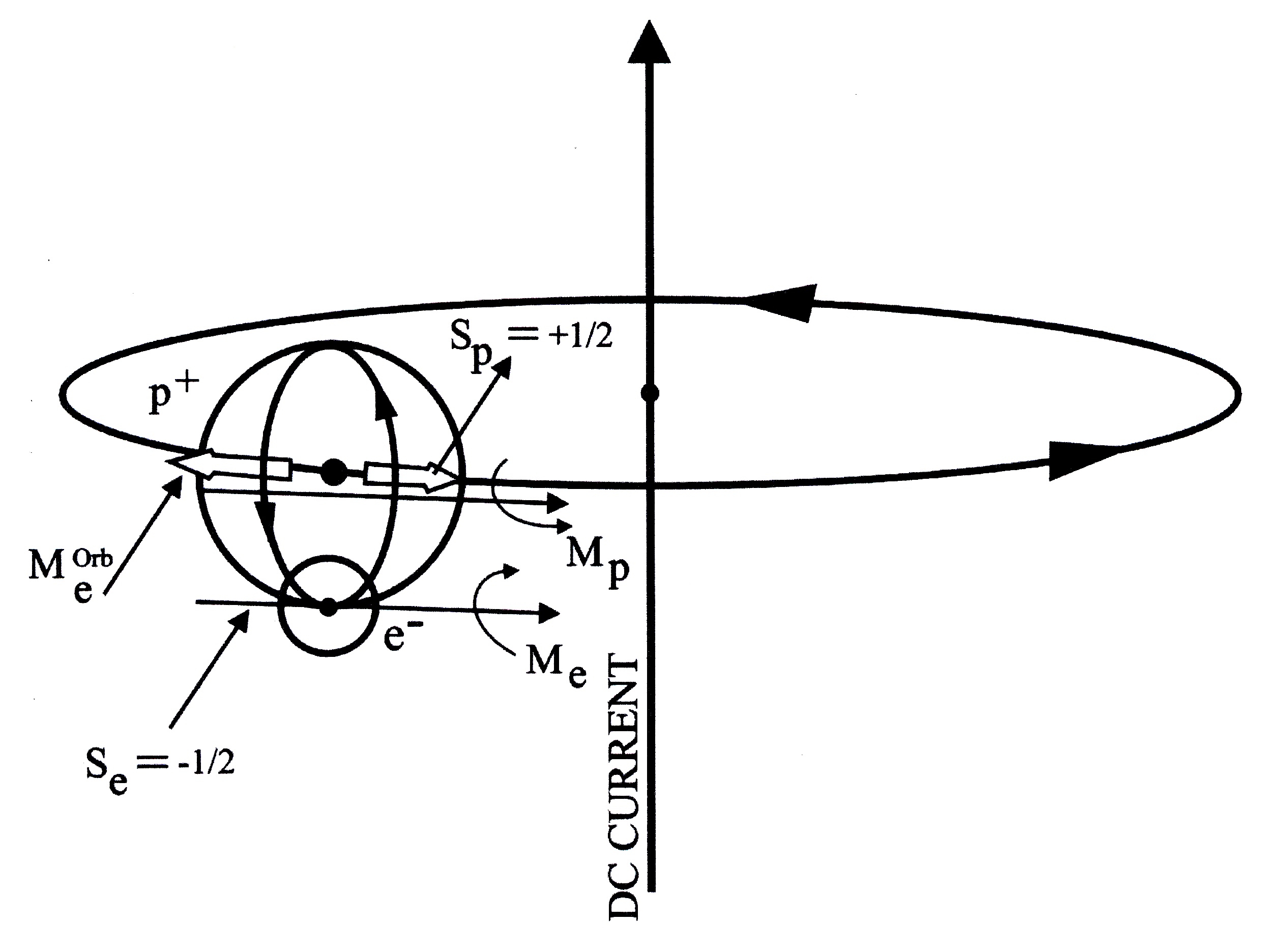
The reader should be aware that, despite the absence of the energy, spin and magnetic anomalies of the neutron, neutroids cannot exist for quantum mechanics and, consequently are assumed as being characterized by the covering hadronic mechanics as an intermediate state prior to the synthesis of the neutron.
6.4E. Interpretation of Don Borghi and Santilli experiments
By remembering the etherino hypothesis of the preceding section, and by ignoring the neutrino hypothesis, Santilli assumes that the energy, spin and magnetic anomalies in the neutron synthesis are accounted for by the reaction
where "a" represents the etherino, namely, the transfer of the missing energy and other quantities either from the ether or from the interior of nuclei, as conditions allow.
In other words, once neutroids are absorbed by nuclei, ordinary neutrons can be produced via a variety of mechanisms, such as the supply of the missing energy, spin and magnetic moment by the nucleus itself, the origination of the missing characteristics from the ether, and other possibilities inessential for this section. In fact, the replacement of the etherino with the antineutrino, in the event desired by academic interests, would leave the content of this section unchanged
Paper 2007 then shows that assumption (6,157) is sufficient, alone, to represent ''all" Don Borghi's data. The open issue is whether the neutron synthesis occurs directly in the nuclei of the activated substances or in the walls of the klystron.
To study this alternative, Santilli assumes the usual symbol N(A, Z, J, u) for ordinary nuclides as currently known, and the symbol Ñ(A, Z, J, amu) for possible anomalous nuclides, namely, nuclides following the absorption of a nuclidoid not existing in available data, called nuclidoids.
Santilli also assume that the binding energy of a neutroid is similar to that of an ordinary nucleon (e.g., BE = 0.0002 amu for the deuteron), since neutroids are assumed to be converted into neutrons when inside nuclei, or to decompose into protons and electrons, thus recovering again the nucleon binding energy.
In this way, Santilli indicates the following possible nuclear reaction for one of the activated substances in Don Borghi's tests
thus recovering conventional activation processes expected in Don Borghi's activation.
By comparison, the application of the above assumption to the steel casing of Don Borghi klystron yields an unknown nuclidoid
since the tabulated nuclide is Fe(58, 26, 0, 57.933).
Needless to say, the anomalous nuclide Fe'(58, 26, 1, 57.941) is expected to be highly unstable and to decay in a variety of possible modes, although they do not appear to provide the source of neutrons necessary to represent Don Borghi data.
This excludes that the neutrons in Don Borghi experiment were synthesized in the walls of his klystron and confirms that the neutrons were synthesized by the activating substances themselves.
6.4F. Santilli's prediction of a new class of nuclides.
Hypothesis (6.157) allows an interpretation of some of Santilli's detections, with the understanding that the anomalous behavior of the detectors, such as the delayed neutron counts, requires special studies and perhaps the existence of additional event not clearly manifested in Don Borghi's tests. To initiate the study, the 2007 paper considers the first possible reaction
namely, we have the prediction that, under transmutation (6.157), the coupling of a neutroid to a proton plus an adequate trigger, creates the ordinary deuteron.
Next, Santilli considers the polycarbonate of Klystron I wall containing about 75 % carbon, for which we have
thus excluding the carbon of the polycarbonate being a source of the detected neutrons. Said polycarbonate contains about 18.88 % oxygen for which we have the reaction yielding an unknown nuclidoid
because the known nuclide is O(17, 8, 5/2, 16.999). The latter reaction too is not expected to provide the neutron counts detected by Santilli. In conclusion, it does not appear that the detected neutrons are synthesized in the interior of the Klystron I or by its walls. The above analysis leaves as the only residual possibility that in Santilli tests, the neutrons are synthesized by the detectors themselves. To study this possibility, Santilli considers the reaction for the He3-activated detector
in which, as one can see, the detection of the neutroids is anomalous if any. Next, for the base of B-activated detectors we have the reactions
that do not appear to behave normally under a flux of neutroids. Finally, we have the reaction for the Li-activated detectors
that do indeed behave in a way fully equivalent as to whether the detection refers to neutroids or neutrons.
However, in the absence of a proper trigger, the etherino is not expected to occur, particularly for light natural and stable nuclides. In this case, it is easy to see that the absorption of a neutroid by a nucleus generally yields a tabulated, thus highly unstable nucleus. For instance, in the absence of the etherino, reaction (6.165) reads
that yields again 2α easily detected buy the Li-activated detector. It is easy to verify that Li*(8, 3, 3/2, 8.022) is not tabulated, thus being a basically new nuclide that, since it has not been detected so far, it is expected to have a very short meanlife. Similar occurrences hold for the re-writing of the preceding reactions without the etherino.
Recall that the neutroid is expected to have strong interactions similar to those of ordinary neutrons, if nothing else, because of its proton content, thus being necessarily absorbed by nuclides when at mutual distances of the order of the strong interactions. Hence, Santilli introduces the following hypothesis (see also next chapter):
HYPOTHESIS 6.4G: The absorption of a neutroid by tabulated neuclides generally produces new highly unstable, untabulated nuclides called "nucleoids" according to the reaction
>From the above reactions we can see a conceivable explanation of the reason the He3-activated detector resulted as being the least active of all 2007 tests. We can also see a plausible reason for the Li-activated detector as being the bests for Santilli's experiment, and that's the reason for mandating its use for any serious reruns.
The conclusion is, therefore, that the neutrons detected in Don Borghi experiment were synthesized by the nuclei of the activated substances, while the neutrons of Santilli experiment were synthesized by the detectors themselves, either by activated substances, or by their casing, the latter expected as being the origin of the delayed detection.
In closing, Santilli warns readers against superficial conclusions, one way or another, no matter how appealing they are, because of the possibility that neutroids could be produced inside Klystron I in clusters much similar, although different than electron clusters, in which case the absorption of neutroid clusters by ordinary nuclei is much more complex then the above analysis and cannot be treated here.
6.4G. Requirements for the re-run of Santilli's experiments
Needless to say, the tests of the neutron synthesis from a hydrogen gas is recommended for conduction under all possible conditions. Nevertheless, in the event these independent tests are used to claim either confirmation or dismissal of Santilli's results, the following conditions must be met to prevent lack of due process.
1) In Santilli's klystron, the electric discharge can be made under a short with no gap between the electrodes, in which case no "entities" are produced and the occurrence could be used to "disprove Santilli experiment." In fact, Santilli elected a transparent PVC klystron precisely to make sure he had an arc since, in case of a short without an arc, with at least a minimal gap of 2-3 mm for at least 4-5 seconds, no "re-run" of Santilli experiment can be scientifically claimed.
2) Santilli's experiment can be repeated with minimal power (say of 1 Kw), the use of a hydrogen gas with minimal pressure (say, a fraction of one psi), creating a real arc with a real gap within the hydrogen gas, resulting in no detection of any type for 2-3 days, thus claiming the "disproof of Santilli experiment." As indicated in the preceding sections, the production of the "entities" and the rapidity of their detection are proportional to the power, the pressure of the hydrogen gas and other factors.
3) Santilli experiment can be repeated with the klystron insulated from external influence such as noise, vibrations, etc., resulting in no detection for days, e.g. with the detector SAM 935, thus claiming the "disproof of Santilli experiment." As indicated in the preceding sections, at times Santilli had to shake the klystron with a rubber hammer, then wait for additional time to finally detect the "entities" outside the klystron, sometime occurring one or two weeks following the arc.
4) Santilli experiment can be easily dismissed with various neutron detectors none of which is Li-activated, then "fixing things" with a sufficiently low DC power and gas pressure, to end up with signals clearly not of neutron type. It has been indicated in the preceding sections that, for reasons unknown at this writing, Li-activation is, by far, the most sensitive to the "entities." Thus, the use of Li-activated detectors is mandatory for any scientific re-run of Santilli's experiment.
5) It is very easy to dismiss Santilli experiment via the mere use of the Tables of Nuclides. In fact, the transmuted nuclides caused by the absorption of a neutroid are not listed in said table and, consequently, they can be claimed not to exist. For the serious scholar we recall that the claim of production in Santilli experiment of true neutron, with consequential claims of producing conventional nuclides, is a direct admission of the continuous creation of matter in the universe for the reasons indicated in Section 6.3. But then, the only possibility of avoiding such extreme implications is to admit that the "entities" are not neutrons, and, consequently, the activated nuclei are not listed in the Table of Nuclides, that is, they are "new" in accordance with Hypothesis 6.4G
As Santilli's puts it: It is generally believed in nuclear physics that all possible nuclides existing in nature, whether stable or unstable, are known. By remembering our extreme ignorance at this writing on the nuclear structure, e.g., our inability for a quantitative representation of nuclear forces, nuclear spins, nuclear magnetic moments, etc., the honest nuclear physicist must admit that our nuclear knowledge is at its infancy, and so much remains to be discovered by young minds of any age.
6.5. REDUCTION OF NUCLEI TO PROTONS AND ELECTRONS.
6.5A. Introduction.
As it is well known, in the same way as Rutherford conceived in 1920 the neutron as a bound state of a proton and an electron, nuclei were also considered in the early part of the 20th century as being bound states of protons and electrons.
The historical successes of quantum mechanics for the atomic structure forced its application also to the nuclear structure, resulting in the denial of Rutherford's conception of the neutron, with consequential denial that nuclei are a bound state of protons and electrons.
Almost needless to say, quantum mechanics has permitted truly historical advances in nuclear physics with impressive verifications continuing to this day, such as the operation of nuclear power plants that are crucially dependent on the use of quantum mechanics. Nevertheless, as stated by Santilli, physics will never admit final theories because, no matter how exact a given theory may appear, its surpassing via broader theories for broader conditions is only a matter of time.
Also, on serious scientific grounds, a theory can be considered as being exact for given systems only when it represents all experimental data of the systems considered from first principles, that is, without the usual adulterations via the throwing into the equations of unknown parameters and arbitrary functions that are fitted from the data themselves, as customary in particle and nuclear physics.
On these serious grounds, quantum mechanics can indeed be considered as being exactly valid for the hydrogen atom, because it represented the totality of the data in an exact way from first principles. By comparison, Santilli has identified in research for about half a century large evidence according to which quantum mechanics can only be considered as being approximately valid for the nuclear structure because of its notorious inability of representing all nuclear data from first principles, including inabilities for exact representations from first principles of nuclear spin, magnetic moments, meanlives and other data, not to mention gross insufficiencies for about one century on the understanding of the nuclear force.
Among the body of evidence accumulated by Santilli, the evidence particularly appealing is the impossibility for the Galilei and the Lorentz-Poincare' symmetries for being exactly valid for the nuclear structure because, in Santilli's words, nuclei do not have nuclei (see Figure 1.2). It is well known that the indicated spacetime symmetries are solely valid for Keplerian systems, that is, as recalled earlier, for a system of massive bodies in point-like approximation moving isolated in vacuum without collision around a heavier bod known as the Keplerian nucleus.
The evident lack of exact validity of conventional spacetime symmetries for the nuclear structure has very deep implications. To begin, it confirms that both, nonrelativistic and relativistic quantum mechanics cannot possibly be exact for the nuclear structure in favor of covering more accurate formulations specifically built for the arena considered.
More deeply, the lack of exact validity of spacetime symmetries implies that the conception of nuclei as bound states of protons and electrons has no exact technical foundation. because these particles are technically characterized via unitary irreducible representations of the Galilei symmetry at the nonrelativistic level and the Lorentz-Poincare' symmetry at the relativistic level, thus leaving the way to broader, more accurate notions of nuclear constituents.
It is evident that Santilli's reduction of the neutron to a hadronic bound state of a proton and an electron directly implies the reduction of all nuclei and, therefore, all matter in the universe, to protons and electrons, for which very scope the construction of hadronic mechanics was proposed in memoir 1978B.
It should, however, be noted upfront that, on technical grounds, the constituents of nuclei are given by protons and electron in their form mutated by contact non-Hamiltonian, thus nonunitary interactions called isoprotons and isoelectrons and technically defined as isounitary irreducible representations of the Lorentz-Poincare'-Santilli isosymmetry.
Needless to say, the current conception of nuclei as bound states of protons and neutrons (nucleons) remains valid, but only as a first approximation of a much deeper physical reality.
In this section, we show that hadronic mechanics not only allows the reduction of nuclei to (iso) protons and (iso) electrons, but also achieves, for the first time known to the authors, a numerically exact and invariant representation of various nuclear data beyond any dream of representation via quantum mechanics.
Needless to say, we cannot possibly review the entire formulation of nuclear physics according to hadronic mechanics. We shall then limit ourselves to illustrate the new nuclear vistas with a representation of all characteristics of the simplest nucleus, the deuteron, and leave the formulations of the remaining aspects of the new nuclear physics to interested colleagues.
6.5B. Santilli's contributions in nuclear physics.
Santilli's main contributions of direct or indirect relevance for nuclear physics are the following:
BASIC CONTRIBUTIONS
[1] On a possible Lie-admissible covering of Galilei's relativity in Newtonian mechanics for nonconservative and Galilei form-noninvariant systems
[2] Need of subjecting to an experimental verification the validity within a hadron of Einstein special relativity and Pauli exclusion principle
[3]
Relativistic hadronic mechanics: nonunitary, axiom-preserving
completion of relativistic quantum mechanics
[4]
Invariant Lie-admissible formulation of quantum deformations
[5]
Nuclear realization of hadronic mechanics
and the exact representation of nuclear magnetic moments
LIE-ISOTOPIC CONTRIBUTIONS
[6]
Closed systems with non-Hamiltonian internal forces
[7]
Generalized two-body and three-bodies systems with non-Hamiltonian internal forces
[8]
Theory of mutation of elementary particles and its application to Rauch's experiment on the spinorial symmetry
[9]
The notion of nonrelativistic isoparticle
[10]
A quantitative isotopic representation of the deuteron magnetic moment
[11]
Theory of mutation of elementary particles and its application to Rauch's experiment on the spinorial symmetry
[12]
Isorepresentation of the Lie-isotopic SU(2) algebra with
application to nuclear physics and local realism,
[13]
Elaboration of the recently proposed test of Pauli's principle under strong interactions,
[14]
Can strong interactions accelerate particles faster than the speed of light?,
[15]
Apparent consistency of Rutherford's hypothesis on the
neutron as a compressed hydrogen atom
[16]
Apparent consistency of Rutherford's hypothesis on the neutron structure via the hadronic generalization of quantum mechanics - I: Nonrelativistic treatment
[17] "Apparent confirmation of Don Borghi's experiment toward the synthesis of neutron from protons and electrons"
[18]
The etherino and/or the neutrino hypothesis
[19]
Possible implications of nonlocal-integral effects for new methods of recycling nuclear waste
LIE-ADMISSIBLE CONTRIBUTIONS
[20]
A possible Lie-admissible time-asymmetric
model of open nuclear reactions,
[21]
Lie-admissible invariant representation of irreversibility for matter and antimatter at the classical and operator level
[22] "The novel 'Intermediate Controlled Nuclear Fusions' and a report on its industrial realization as permitted by hadronic mechanics"
[23]
Experimental confirmation of the novel intermediate controlled nuclear fusions without harmful radiations
[24]
Verification of Santilli's intermediate nuclear fusions without harmful radiation
MONOGRAPHS
[25] "Foundations of Theoretical Mechanics, I: The Inverse Problem in Newtonian Mechanics"
[26] "Foundations of Theoretical Mechanics, II: Birkhoffian Generalization of Hamiltonian Mechanics"
[27] "Isotopic Generalization of Galilei and Einstein Relativities",
Volume I: "Mathematical Foundations"
[28] "Isotopies of Galilei and Einstein Relativities"
Vol. II: "Classical Foundations"
[29] "Elements of Hadronic Mechanics", Vol. I: "Mathematical Foundations"
[30] "Elements of Hadronic Mechanics"
Vol. II: "Theoretical Foundations"
[31]
The Physics of New Clean Energies and Fuels According to Hadronic Mechanics.
[32] "The structure of the neutron as predicted by hadronic mechanics"
[33] Hadronic Mathematics, Mechanics and Chemistry, Volumes I, II, III, IV and V:
6.5C. Review of basic nuclear contributions.
Recall that the quantum mechanical description of nuclear physics is centered on Heisenberg's equations characterizing the time evolution of an observable A in the following infinitesimal and finite form
R. M. Santilli, Hadronic J. Vol. 1, 223-423 (1978)
R. M. Santilli, Hadronic J. Vol. 1, 574-901 (1978)
R. M. Santilli,
Found. Phys. Vol. 27, 625-729 (1997)
R. M. Santilli,
Found. Phys. Vol. 27, 1159- 1177 (1997)
R. M. Santilli,
Intern. J. of Phys. Vol. 4, 1-70 (1998)
R. M. Santilli,
ICTP preprint # IC/91/259 (1991)
published in "Santilli's 1991 Papers at the ICTP", International Academic Press (1992)
R. M. Santilli,
ICTP preprint # IC/91/264 (1991)
published in "Santilli's 1991 Papers at the ICTP", International Academic Press (1992)
R. M. Santilli,
ICTP preprint # IC/91/265 (1991)
published in "Santilli's 1991 Papers at the ICTP", International Academic Press (1992)
R. M. Santilli,
ICTP preprint # IC/91/265 (1991)
published in "Santilli's 1991 Papers at the ICTP", International Academic Press (1992)
R. M. Santilli,
in "Proceedings of the International Symposium 'Dubna Deuteron-93'", Joint Institute for Nuclear Research, Dubna, Russia (1994)
R. M. Santilli,
ICTP preprint # IC/91/46 (1991)
published in "Santilli's 1991 Papers at the ICTP", International Academic Press (1992)
R. M. Santilli,.
Acta Appliucandae Mathematicae Vol. 50, 177-190 (1998)
R. M. Santilli,
Lettere Nuovo Cimento Vol. 33, 145 (1982)
R. M. Santilli,
Hadronic J. Vol. 13, 513-531 (1990)
R. M. Santilli,
ICTP preprint # IC/91/47 (1992)
published in "Santilli's 1991 Papers at the ICTP", International Academic Press (1992)
R. M. Santilli, Hadronic Journal Vol. 30, 709 (1997).
R. M. Santilli,
Foundation of Physics, Vol. 37, 670 (2007)
R. M. Santilli,
in the proceedings of "Large Scale Collective Motion of Atomic Nuclei", G. Giardina, G. Fazio and M. Lattuada, Editors, World Scientific pages 549-556 (1996)
R. M. Santilli,
Lettere Nuovo Cimento Vol. 37, 337-344 (1983)
Ruggero Maria Santilli
Nuovo Cimento B Vol. 121, p. 443-595 (2006)
R. M. Santilli, Hadronic Journal Vol. 31, 115 (2008).
R. M. Santilli,
In press at New Advances in Physics (2010)
and the production of magnecular clusters
Robert Brenna, Theodore Kuliczkowski, Leong Ying
Princeton Gamma-Tech Instruments, Princeton, New Jersey,
In press at New Advances in P{physics.
R. M. Santilli, Springer-Verlag (1978)
R. M. Santilli, Springer-Verlag (1982).
R. M. Santilli,
Hadronic Press (1991)
R. M. Santilli,
Hadronic Press (1991)
R. M. Santilli
Ukraine Academy of Sciences (1995)
R. M. Santilli,
Ukraine Academy of Sciences (1995)
R. M. Santilli,
ICTP preprint # IC/91/47 (1992)
published in a special issue of the Journal of New Energy, Volume 4, pages 1-324 (1999)
R. M. Santilli, website (2006).
R. M. Santilli, International Academic Press (2008)
where: the brackets [A, H] characterize a Lie algebra; the finite time evolution constitutes a Lie group characterized by a unitary transform on a Hilbert space, and the Hamiltonian H characterizes the total energy
Under these assumptions, the sole possible representation of the nuclear force is that via action-at-a-distance forces derivable from a potential, resulting in a sequence of failed attempts during the 20th century to achieve a final understanding of the nuclear force, with implausible extremes up to the use of a very large number of potentials, as in Eq. (1.5), i.e.,
+ V11 + V12 + V13 + V14 + V15 + V16 + V17 + V18 +
+ V19 + V20 + V21 + V22 + V23 + V24 + V25 +
+ V26 + V27 + V28 + V29 + V30 + V31 + V32 +
+ V33 + V34 + V35 + ...
Due to the manifest insufficiency of the above representation, Santilli main assumption is that, when part of a nuclear structure, nucleons are in conditions of partial mutual penetration and overlapping of their charge distributions as established by comparing nuclear volumes with the charge volumes of nucleons. Consequently, in additional to conventional (e.g., Coulomb) interactions derivable from a potential, nuclei must admit non-potential, thus non-Hamiltonian internal forces, generally called in the 20th century "nonconservative forces."
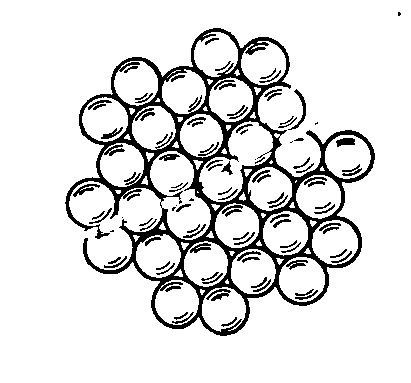
Figure 6.24. A view often used by Santilli to illustrate that nuclei are composed by extended constituents in contact with each other, thus prohibiting that the nuclear force is solely of potential type because the latter solely applies for action-at-a-distance forces among point-like particles. The need for a nonpotential component in the nuclear force motivated the birth and construction of hadronic mechanics.
Santilli proposed the construction of hadronic mechanics for the time invariant description of nuclear structures with both Hamiltonian and non-Hamiltonian internal forces. For this purpose, he first proposed in memoir [1] the Lie-isotopic generalization of Lie's theory in its various branches (universal enveloping associative algebras, Lie algebras, and Lie groups) into a covering theory today known as Santilli Lie-isotopic theory based on the axiom-preserving product [A, B]* = ATB - BTA, where T is a new Hermitean, positive-definite operator independent from H characterizing the inverse of the new unit I* = 1/T > 0 (see Chapters 2 and 3).
In memoir [1], Santilli also proposed the Lie-admissible broadening of his Lie-isotopic theory characterized by the product (A, B) = ARB - BSA, where R and S are also new operators independent from H, which product is Lie-admissible in the sense that the attached antisymmetry brackets [A, B]* = (A, B) - (B, A) is Lie-isotopic. This resulted in a yet broader theory today known as Santilli Lie-admissible theory.
Thanks to these necessary mathematical advances, in the subsequent memoir [2] of the same year, Santilli proposed two generalizations of quantum mechanics for nuclear physics, the first of Lie-isotopic character, based on the following lifting of Heisenberg equations today known as Heisenberg-Santilli Lie-isotopic equations
The above dynamical equations are at the foundation of the Lie-isotopic branch of nuclear mechanics. They imply that nuclei are represented via two operators, a con conventional Hamiltonian representing physically valid potentials, plus the isotopic operator T representing contact non interactions not derivable from a potential,
where F(r) function is positive-definite and the T operator, here presented in a simple realization, is restricted to recover the identity at all distances greater than 10-13 cm, so as to recover quantum mechanics uniquely and unambiguously.
In the same memoir [2], Santilli proposed the broader Lie-admissible generalization of his Lie-isotopic equations characterized by equations today known as the Heisenberg-Santilli Lie-admissible equations
which are at the foundation of the broader Lie-admissible branch of hadronic mechanics, further broadened into the hyperstructural branch for biological structure and the isodual Lie-isotopic, isodual Lie-admissible and isodual hyperstructural branches for antimatter hereon ignored.
In the latter case, nuclear processes are represented by three operators, the Hamiltonian H and the Lie-admissible operators R and S, e.g., of the type
where the latter expressions are restricted to the condition of admitting the isotopic formulation as a particular case for R = S = T > 0, and of recovering quantum mechanics identically and unambiguously at all distances bigger than 10-13 cm. The condition R = S† originates from technical condition of consistency (see later on).
The reason for two, rather than one, generalization of quantum formalisms is the following. The Lie brackets [A, B] and the Lie-Santilli bracket [A, B]* are invariant under anti-Hermiticity,
Consequently, both, quantum mechanics and the Lie-isotopic branch of hadronic mechanics are invariant under time reversal. Consequently, both mechanics are ideally suited to represent isolated nuclei verifying all conventional conservation laws, including that of the energy,
the only novelty of the Lie-isotopic theory is the admission of internal nonpotential forces not possible for quantum mechanics.
More technically, Santilli proved that all conventional conservation laws of total quantities are preserved in the Lie-isotopic mechanics because the generators of basic spacetime symmetries, representing precisely such conservation laws, remain unchanged in the transition from the Lie to the Lie-isotopic symmetries.
The broader Lie-admissible formulation is necessary because, unlike the structure of stable nuclei, nuclear reactions are generally irreversible over time. Consequently, the representation of, say, a nuclear fusion
via both the Lie and the Lie-isotopic mechanics implies the existence of a finite probability of the existence of the time-reversal spontaneous disintegration of the synthesized nucleus into the original nuclei
in gross violation of energy conservation, causality and other basic laws. To avoid these catastrophic inconsistencies, Santilli conceived hadronic mechanics since its inception with the Lie-admissible branch because it is irreversible over time due to the property R ≠ S, thus preventing no finite probability of inverse reaction (6.178). Rather than conservation law (6.176), the Lie-admissible branch characterizes the time rate of variation of physical quantities, such as that of the energy,
The latter characterization was proposed in memoir [1] via advanced mathematics based on Lie-admissible transformation group we cannot possibly review here.
Following the achievement of the above formulations, it became known by Santilli and other scholars that nonunitary theories formulated via the mathematics of unitary theories (Hilbert spaces, conventional numerical fields, differential calculus, etc.) are afflicted by the so-called Theorems of Catastrophic Mathematical and Physical Inconsistencies of Noncanonical and Nonunitary Theories reviewed in details in Section 3.9, including the lack of preservation of the same numerical predictions under the same conditions at different times, lack of preservation of Hermiticity (thus, observability) over time, violation of causality, and other inconsistencies.
The resolution of these inconsistencies required decades of research, including the construction of two new mathematics, the first underlying the Lie-isotopic theories known as isomathematics, and the second underlying the lie-admissible theories known as genomathematics, reviewed in Chapter 2.
Following the construction of the needed new mathematics, and only thereafter, Santilli achieved the resolution of the inconsistency theorems for the Lie-isotopic case in memoir [3] of 1997 and for the Lie-admissible case in paper [4] of the same year. The formulation of hadronic mechanics, specifically, for nuclear physics was presented in memoir [5] of 1998.
In summary, to understand the treatment of nuclear physics via hadronic mechanics, one must first identify first whether the structure or process considered is reversible or not over time (invariant or not under time reversal). In the former case the Lie-isotopic formalism must be used with underlying isomathematics, and in the latter case the broader Lie-admissible formalism must be used with underlying genomathematics.
6.5D. Review of Lie-isotopic nuclear contributions.
Prior to Santilli's studies, it was popularly believed that total conservation laws are solely verified by systems with conservative/potential internal forces, thus leading to the quantum treatment of nuclear structures since quantum mechanics can notoriously represent only potential forces. Santilli went to great lengths in disproving this belief, and established the existence of closed-isolated non/Hamiltonian systems, namely, systems with conservative-potential and nonconservative-nonpotential internal forces. In the latter systems, we merely have internal exchanges, in general, of all physical quantities in such a way that they cancel each other, since the system is assumed as being isolated, resulting in total conservation laws.
This important discovery, which is at the foundation of the Lie-isotopic representation of isolated stable nuclei, was studied in detail in the two monographs [25,26] published by Springer-Verlag, Heidelberg, Germany. When visiting in 1991 Nobel Laureate Abdus Salam (in the the last months of his life) at the International Center for Theoretical Physics (ICTP) in Trieste, Italy, Santilli wrote paper [6] on closed non-Hamiltonian system (see also the review in Section 3.11D)
To illustrate the differences between closed Hamiltonian and non-Hamiltonian systems, Santilli has repeatedly compared the former to planetary systems, where all forces are clearly at a distance derivable from a potential, while, by contrast, non-Hamiltonian systems can be compared to the structure of Jupiter that, when isolated from the rest of the universe, clearly verifies all conventional total conservation laws, yet its interior structure has highly nonconservative internal effects visible via a telescope, such as tornado in the upper atmosphere with locally varying angular momenta. Santilli then assumes the planetary structure as a classical counterpart of the atomic structure, as customary, and the structure of Jupiter as a classical counterpart of the nuclear structure of hadrons, nuclei and stars.
During the same 1991 visit at the ICTP, Santilli also wrote paper [7] to illustrate that, rather unexpectedly, contact internal forces among extended constituents, rather than complicating structure equations, generally allow exact analytic solutions. For the two-body case of constituents with equal masses, the structure equation for Hamiltonian systems is rather complex with a number of elliptic orbits. When contact interactions are admitted forcing the constituents to remain at the same mutual distance, as it is the case for nuclear forces, the circle is the sole stable orbit, thus allowing a rather simple exact analytic solution. Similarly, three-body Hamiltonian systems do not admit analytic solutions, as well known. By comparison, when contact interactions are admitted, the system is turned into a restricted three-body with rather simple analytic solutions.
The next basic notion needed for an understanding of the new nuclear theory is that of isoparticles indicated in the preceding section. Unfortunately, this notion is very advanced since it requires a technical knowledge of Santilli Lie-isotopic theory. Nevertheless, it is important to have at least a conceptual outline. As it is well known, action-at-a-distance interactions, such as electromagnetic interactions, generally alter the kinematics characteristics of particles, but they do not change the intrinsic characteristics, such as spin, charge, mass, etc. By comparison, as shown in the preceding sections 6.2 and 6.3, contact non-Hamiltonian interactions generally alter all characteristics of particles, including mass, spin, charge, etc. trivially, because the particle considered is under partial or total immersion within other particles, thus generally exchanging with the latter all possible physical characteristics.
Santilli has also dedicated particular care to the quantitative treatment of the notion of constituents of closed non-Hamiltonian systems called isoparticles, technically characterized by the notions of mutation or isorenormalization. A readable account is presented in papers [8,9] also written at the ICPT in 1991. It should be indicated that the primary objective of the notion of isoparticle is to assure that, for example, an isoelectron in the core of a star violates the rotational symmetry as a necessary condition to prevent the nonscientific belief that an electron in the core of a star can orbit with a conserved angular momentum.
The implications of the notion of closed non-Hamiltonian systems with mutated constituents are truly far reaching. To begin, nucleons must be perfectly rigid for quantum mechanics, evidently as a necessary condition not to violate a pillar of the theory, the rotational symmetry. At any rate, quantum mechanics is known to be incompatible with the deformation theory. Santilli claims that such a rigid notion of nucleons is unrealistic because there exist no rigid bodies in nature, the sole debatable issue is the amount of deformation of nucleons under given external conditions. Hence, Santilli replaces the quantum notion of perfectly rigid nucleons with that of isonucleons, that is, isoprotons and isoneutrons that, as such, do admit deformations of their charge distribution
since their shape verifies the covering rotational symmetry admitting indeed all possible deformations. In turn, such a deformability readily permits the first known exact numerical representation of nuclear magnetic moments from axiomatic first principles without ad hoc adulterations via arbitrary parameters and the like (see papers [10,11] and Section 5.3).
Rather surprisingly, conventional quantum symmetries are not "destroyed," but reconstructed as being exact at the covering Lie-isotopic level. Consider, for instance, the deformation of the perfect sphere on an Euclidean space with conventional metric δ = Diag. (1, 1, 1),
Such a deformation causes the breaking of the rotational symmetry SO(3) when treated via conventional mathematics with unit I = Diag. (1, 1, 1). However, when the same deformation is treated via the new mathematics based on isounit
the covering isorotational symmetry SO*(3) leaves invariant the ellipsoids while being isomorphic to the original symmetry SO(3). This is due to the fact that the deformation of the semi axes, represented by the isotopic element T*, is entirely compensated by the inverse values of the isounit,
resulting in the perfect sphere in isospace over isofields called the isosphere. Rather than being broken, the rotational symmetry is reconstructed as being exact, although under the proper mathematical formulation.
The reconstruction of the exact rotational symmetry also applies to all spacetime and other symmetries. In fact, the basic spacetime symmetries of the new nuclear structure, the Galilei-Santilli isosymmetry for nonrelativistic treatments and the Lorentz-Poincare'-Santilli isosymmetry for relativistic counterparts, are isomorphic to the original forms as a very condition to have consistent "isotopies" (see monographs [27,28] and original contributions quoted therein). Therefore, rather than "destroying" the basic spacetime symmetries of the 20th century, Santilli has dramatically broadened their conditions of applicability.
To further illustrate the non triviality of these advances, we should note that statements such as "the SU(2) nuclear isospin symmetry is broken by electromagnetic interactions" have been proved as being erroneous. In fact, Santilli has reconstructed in paper [12] the isotopic SU* symmetry and proved that it is exactly valid under electromagnetic interactions while being isomorphic to the conventional SU(2) symmetry. The mechanism is quite simple and essentially consists in embedding in the isounit all symmetry breaking terms.
The notion of isonucleons has additional very deep implications. One of them is the inapplicability of Pauli's exclusion principle in the nuclear structure pointed out by Santilli in the very title of memoir [2] and then studied in detail in various works, such as paper [13]. In essence, Santilli argues that Pauli's principle is definitely valid for fermions in a quantized energy level of an atomic structure. In the transition to a nuclear structure, we have the loss of quantized orbits to be replaced by shells, the general loss of the Fermionic character by the isonucleons and other feature that prohibit the very definition of Pauli's principle in the interior of a nucleus, let alone its verification. Note that Santilli stresses the inapplicability of Pauli's principle in nuclear physics and not its "violation."
As an additional, far reaching implications,. we should indicate that the maximal speed of nuclear constituents is not limited by the speed of light in vacuum. This occurrence was predicted by Santilli in paper [14] of 1982 on grounds that the maximal causal speed c of special relativity is based on the sole existence of interactions admitting a potential energy. For the case of contact interactions the situation is dramatically different because contact interactions can accelerate particles without energy considerations, as it is the case of a balloon accelerated by wind in atmosphere. The absence of a potential energy then permits contact interactions of causal accelerations beyond the speed of light in vacuum.
Subsequently, Santilli provided great efforts for systematic theoretical studies of maximal causal speeds in the interior of non-Hamiltonian systems. In essence, the basic invariant of the Lorentz-Poincare'-Santilli isosymmetry is the light isocone here presented in two dimensions for simplicity
Consequently, the maximal causal speed is given by
that,as such can be smaller, equal or bigger than c (see monographs [27-30] for details).
Additionally, Santilli has conducted comprehensive experimental studies reported in Vol. IV of series [33] (see also the review in Chapter 5) according to which the fit of experimental data from first axiomatic principles without ad hoc adulterations indicates that the maximal causal speed within hyperdense media, thus including in the interior of nuclei, is bigger than c.
Papers [15-18] have been reviewed in Section 6.3 and are at the foundation of the reduction of nuclei to protons and electrons. Paper [19] deals with the stimulated recycling of radioactive nuclear waste and will be considered in the next chapter.
6.5E. Review of Lie-admissible nuclear contributions.
Dissipate processes in nuclear physics have been known since the inception of the theory. However, dissipation is incompatible with the axioms of quantum mechanics, since they describe conservation laws of Hermitean, thus observable quantities. To bypass this occurrence, a widespread approach to dissipativity in the 20th century nuclear physics has been the use of "imaginary potential" with Hamiltonians of the type
Santilli pointed out in paper [20] of 1983 that under the above assumption, we have the follolwing finite and infinitesimal time evolution of a Hermitean operator A(t)
namely, Heisenberg's unitary time evolution (6.168) characterized by the Lie brackets [A, H] is turned into a nonunitary time evolution characterized by the triple system [A, H. H†], namely, a structure which is incompatible with the axioms of quantum mechanics.
To begin, "imaginary potentials" have no known physical meaning of any type. Next, being nonunitary, time evolution (6.186) verifies the Theorems of Catastrophic Inconsistencies of Section 3.9. Finally, being non-Hermitean, the Hamiltonian is no longer observable, namely, time evolution (6.186) loses the observability for the very effect to be measured, the nonconservation of the energy.
To resolve these inconsistencies, paper [20] proposed the maintaining of the Hermiticity of the Hamiltonian as a necessary condition for its observability, and the use of the Lie-admissible time evolution (6.173) that assures indeed the dissipation of the observable energy, Eq. (6.179), by recovering in this way a fully consistent theory, although at the level of the covering hadronic mechanics.
In any case, the abandonment of quantum mechanics in favor of a covering mechanics for dissipative nuclear events is beyond any possible scientific doubt. The only open scientific issue is the apropriate covering theory. Santilli suggested the Lie-admissible branch of hadronic mechanics for the representation of dissipative nuclear events because of its "direct universality" for all possible nonconservations (representation of all possible systems in the frame of the observer), as well as because it is the only known formulation for nonconservative events achieving invariance over time, thus bypassing the Theorems of Catastrophic Inconsistencies.
The final invariant representation of all nonconservative processes, including dissipative nuclear events in particular, was reached by Santilli in the historical memoir [21] that is the apex of his research achievement since it includes as particular cases Lie-isotopic and quantum formmulations. Particulalry instructive for nuclear physicists is the study of the last section of memoir [21] with numerous examples of invariant representation of dissipative systyems, as well as the "direct universality" in the representation of all possible non conservative forces not derivable from a potential with the operators R and S acting on a Hermitean but non-conserved Hamiltonian.
Papers [22-24] deal with a a novel approach to nuclear fusion, thus being crucially dependent, for evident consistency, on the Lie-admissible formulation. Since these papers deal with a new form of clean energy, they will be reviewed in the next chapter.
6.5F. Reduction of the deuteron to two protons and one electron.
6.5Fa. Foreword.
We are now sufficiently equipped to review Santilli's structure model of the deuteron as a hadronic bound state of two protons and one electron verifying the laws and symmetries of hadronic mechanics. In fact, to prevent major misjudgments, its understanding requires the prior knowledge of the following aspects treated previously:
1) The deuteron is a stable light, natural isotope that, as such, is reversible over time, namely, its structure equation must be invariant under time reversal. Under the assumption of internal potential/Hamiltonian and contact/non-Hamiltonian forces, the sole known invariant treatment is that via Lie-isotopic formulations and basic dynamical equations (6.171);
2) Therefore, by using his structure model of the proton studied in Section 6.3, Santilli assumes the quantum mechanical structureless of the deuteron (hereon denoted "d")
as valid in first approximation, and reduces the deuteron to two protons and one electron according to the structure
with the understanding that the constituents are isoparticles, namely, two isoprotons and one isoelectron, technically defined as isounitary irreducible representation of the Galilei-Santilli isosymmetry for nonrelativistic treatments and of the Lorentz-Poincare'-Santilli isosymmetry for relativistic formulations with consequential generally mutated intrinsic characteristics of mass, charge, spin, etc.;
3) Contrary to expectations, contact interactions generate a special version of restricted three body system that admits an exact analytic solution.
In this section we shall first review the several insufficiencies of quantum mechanics for a quantitative representation of very basic experiential data on the deuteron and then review their exact and invariant representation via Santilli isomechanics and underlying isomathematics.
6.5Fb. Insufficiencies of quantum mechanics for the deuteron structure.
Despite the widespread acceptance of quantum mechanics throughout the 20th century as providing the final representation of nuclear structures, we begin our analysis with the review of the inability by quantum mechanics to represent the following basic data of the simplest possible nucleus, the deuteron, with embarrassing deviations for large nuclei such as the zirconium:
1) Quantum mechanics has been unable to represent the stability of the deuteron. This is evidently due to the natural instability of the deuteron. The unsolved problem is due to the absence in the technical literature of quantitative numerical proofs that, when bonded to a proton, the neutron cannot decay, as an evident condition for stability. Except for philosophical-political statements, the stability of the deuteron has been left fundamentally unexplained by quantum mechanics to this day (see Figure 1 for more details).
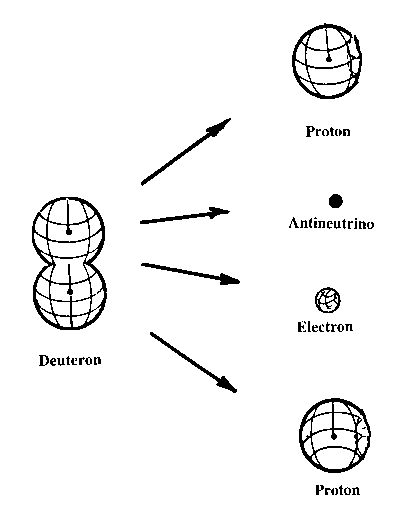
Figure 6.25. A reproduction of the drawing used by Santilli to illustrate the inability by quantum mechanics to represent the stability of the deuteron since the neutron is naturally unstable and, therefore, the deuteron should decay into two protons, an electron and the hypothetical antineutrino. No quantitative argument is known to the authors explaining the reason for the neutron to become stable when coupled to a proton. By comparison, Santilli's three body model of the deuteron represents its stability ab initio.
2) Quantum mechanics has been unable to represent the spin 1 of the ground state of the deuteron. The basic axioms of quantum mechanics require that the most stable bound state of two particles with the same spin is that with SPIN ZERO. No such state has been detected in the deuteron. Therefore, following one century of research, quantum mechanics has been unable to represent the spin 1 of the ground state of the deuteron except, again, for political-nonscientific views (see Figure 2 for more details).
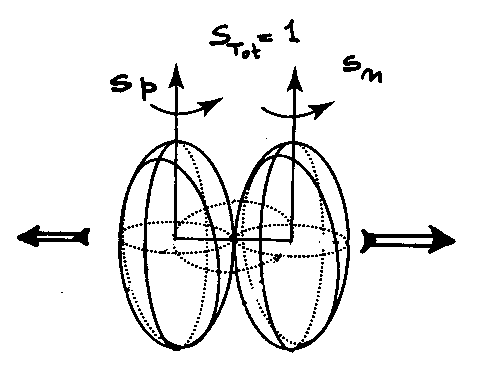
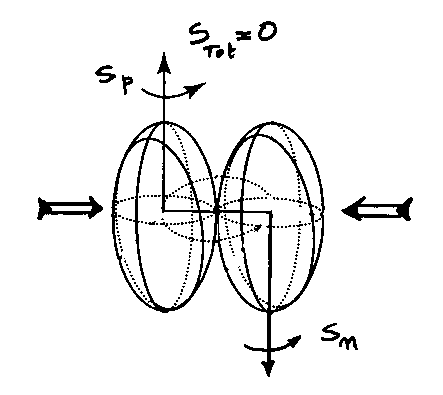
Figure 6.26. Reproduction of the original drawing used by Santilli to illustrate the impossibility of quantum mechanics to represent the spin 1 of the deuteron in a way compatible with its size. In fact, spin 1 can solely be achieved with a triplet coupling (top view), in which case no stable nucleus is conceivable due to very strong repulsive forces at the distance of nuclear forces. The only stable state is the singlet (bottom view), but in this case the total angular momentum is zero, in disagreement with experimental evidence.
3) Quantum mechanics has been unable to reach an exact representation of the magnetic moment of the deuteron. After about one century of research, nonrelativistic quantum mechanics misses 0.022 Bohr units corresponding to 2.6% of the experimental value. Relativistic corrections reduce the error down to about 1% but under highly questionable theoretical assumptions, such as the use for ground state of a mixture of different energy levels that are assumed to exist without any emission or absorption of quanta as requested by quantum mechanics. Embarrassing deviations occur for the magnetic moments of heavier nuclei.
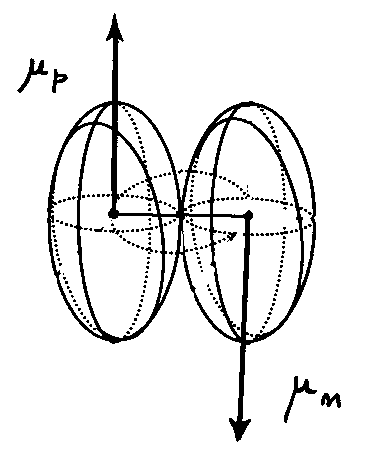
Figure 6.27. Reproduction of the figure used by Santilli to illustrate the impossibility by quantum mechanics to achieve an exact representation of the deuteron magnetic moment in a way compatible with the other characteristics such as total angular momentum, and charge radius.
4) Quantum mechanics has been unable to identify the physical origin of the attractive force binding together the proton and the neutron in the deuteron. Since the neutron is neutral, there is no known electrostatic origin of the attractive force needed for the existence of the deuteron. As a matter of fact, the only Coulomb force for the proton-neutron system is that of the magnetic moments, which force is REPULSIVE for the case of spin 1 with parallel spin. Therefore, a "strong" force was conjectured and its existence was subsequently proved to be true. Nevertheless, the physical origin of such strong force has remained unidentified following one century of research via quantum mechanics. Particularly mysterious remain the "exchange forces," namely, forces originating from the exchange of protons and neutrons.
5) Quantum mechanics has also been unable to treat the deuteron space parity in a way consistent with the rest of the theory. The experimental value of the space parity of the deuteron is positive for the ground state, because the angular momentum L is null. However, in the dream of achieving compatibility of the deuteron phenomenology with quantum mechanics, nuclear physicists assume for the calculation of the magnetic moment that the ground state is a mixture of the lowest state with L = 0 with other states in which the angular momentum is not null, thus implying an embarrassing incompatibility of these calculations with the positive parity of the ground state.
In conclusion, after about one century of research, quantum mechanics has left unresolved fundamental problems even for the case of the smallest possible nucleus, the deuteron, with progressively increasing unresolved problems for heavier nuclei. Following these insufficiencies, any additional belief on the final character of quantum mechanics in nuclear physics is a sheer political posture in disrespect of the societal need to search for a more adequate mechanics.
Not only quantum mechanics is not exactly valid in nuclear physics, but the very assumption of neutrons as nuclear constituents is approximately valid since neutrons are composite particles. Therefore, the main objective of this chapter is the identification of stable, massive physical constituents of nuclei and their theoretical treatment that admits in first approximation the proton-neutron model, while permitting deeper advances.
The replacement of protons and neutrons with the hypothetical quark is mathematically significant, with the clarification that, in Santilli's view, quarks cannot be physical particles because, as stresses several times in this presentation, quarks are purely mathematical representations of a purely mathematical symmetry realized in a purely mathematical internal unitary space without any possible formulation in our spacetime (because of the O'Rafearthaigh's theorem).
Consequently, quark masses are purely mathematical parameters and cannot be physical inertial masses. As also stressed several times, on true scientific grounds, inertial masses can only be defined as the eigenvalues of the second order Casimir invariant of the Lorentz-Poincare' symmetry. But this basic symmetry is notoriously inapplicable for the representation of quarks because of their particular features. Therefore, quark "masses" cannot have inertia.
Additionally, Santilli points out that the hypothetical orbits of the hypothetical quarks are excessively small to allow an exact representation of nuclear magnetic moments via their polarization. In fact, various attempts have been made in representing magnetic moments when reducing nuclei to quarks with the result of bigger deviations from experimental data than those for the proton-neutron structure. Similar increases of the problematic aspects occur for all other insufficiencies of quantum mechanics in nuclear physics. Consequently, the reduction of nuclei to quarks will be ignored hereon because of its excessive deviation from solid physical foundations as well as experimental data.
In conclusion, quarks can indeed be considered as replacements of protons and neutrons, with the understanding that nuclei made up of quarks cannot have any weight, since, according to Albert Einstein, gravity can solely be defined for bodies existing in our spacetime.
6.5Fc. Conception of the deuteron structure.
Recall that the nuclear force solely applies up to the distance of 10-13 cm, which distance coincides with the charge radius of the proton as well as the electron wavepacket, and that the sole stable orbit for the two protons under contact strong interactions is the circle. The size of the deuteron then forces the charge distributions of two protons as essentially being in contact with each other (of course, in first nonrelativistic approximation). It then follows that the electron is totally immersed within a proton, expectedly exchanging its penetration from one proton to the other.
Recall also that: the spin of the deuteron in its ground state is 1; the spin of the protons (assumed in first approximation as being un-mutated) is 1/2; the spin of the isoelectron is 1/2; and that the mutated angular momentum of the isoelectron is -1/2. These features suggested Santilli to assume the structure of the deuteron as being composed of two un-mutated protons with parallel spins rotating around the central isoelectron to allow the triplet coupling, and then the two coupled particles in line have an orbital motion around the isoelectron at the center, resulting in the first approximation in the following hadronic structure model of the deuteron [5] (see also monograph [31] and website [32])
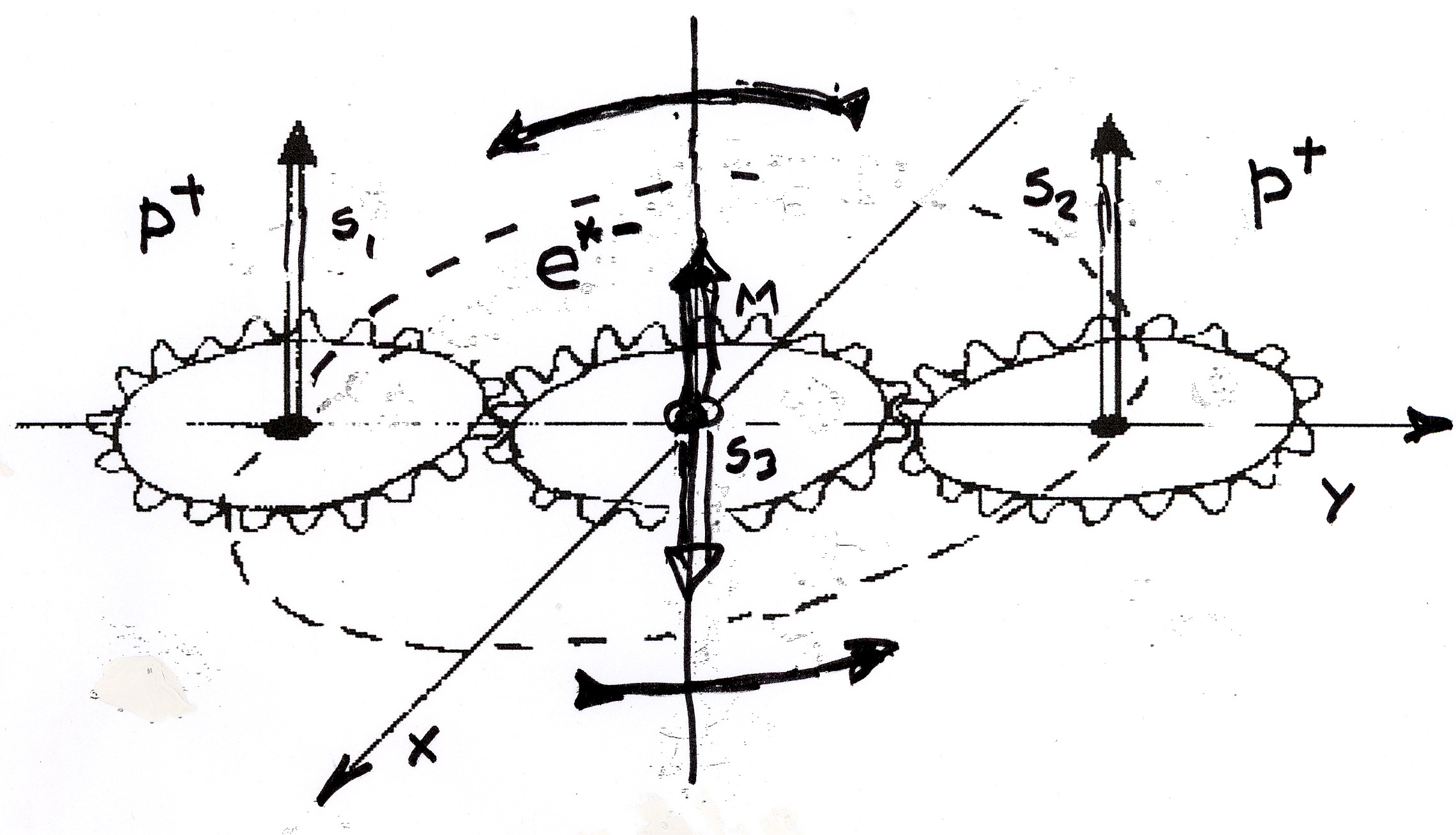
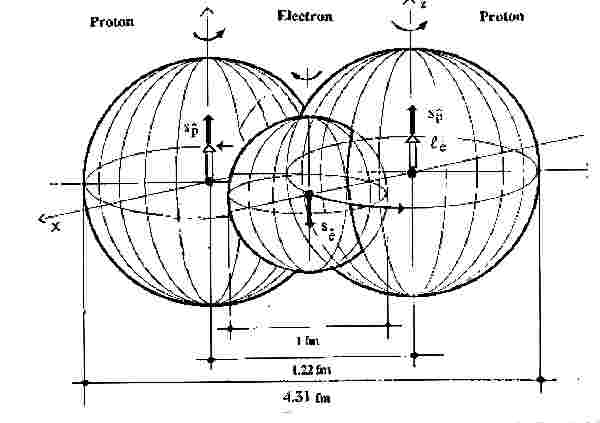
Figure 6.28. Reproduction of two original drawings used by Santilli to illustrate his conception of the structure of the deuteron as a restricted three body of two un-mutated protons (due to their weight) and one mutated electron. As reviewed in detail in the following sections, the top view uses the very effective "gear model" to avoid the highly repulsive triplet couplings, while the bottom view is the same as the top view, the particles being represented with overlapping spheres.
As we shall see, irrespective of the resolution of the objections against Rutherford's conception of the neutron presented in Section 6.3, a three-body structure provides the only known consistent representation of all characteristics of the deuteron, first achieved by R. M. Santilli in Ref. [5] of 1998.
6.5Fd. Representation of the stability of the deuteron.
As indicated earlier, the lack of a quantitative representation of the stability of the deuteron when composed by the stable proton and the unstable neutron has been one of the fundamental problems left unsolved by quantum mechanics in about one century of research.
By comparison, protons and electrons are permanently stable particles. Therefore, structure model (6.189) resolves the problem of the stability of the deuteron in a simple, direct, and visible way. The deuteron has no unstable particle in its structure and, consequently it is stable due to the strength of the nuclear force.
In fact, as shown below, the Coulomb and contact attractive forces in pair-wise singlet couplings proton-isoelectron are so "strong" to overcome Coulomb repulsion among the two protons and form a bound state that is permanently stable when isolated, as already established for the valence bond and Cooper pairs of identical electrons (Chapter 5).
6.5Fe. Representation of the deuteron size.
Experimental data have established that the proton has the following values for the charge radius and diameter (size)
A value of the size of the deuteron that can be found in the literature is given by
Structure model (6.189) does indeed fully represent the above data in accordance with Figure 6.28. In fact, the above data indicate that the charge radii of the two protons are separated by approximately 1.1 fm, namely, an amount that is fully sufficient, on one side, to allow the triplet alignment of the two protons as in the upper part of Figure 6.28 and, on the other side, to generate contact nonlocal effects from the penetration of the wave packet (here referred to the square of the probability amplitude) of the central spinning electron within the two peripheral protons.
6.5Ff. Representation of the deuteron charge.
At a first glance, model (6.189) trivially represents the deuteron positive charge +e. Nevertheless, its quantitative representation is not trivial at a deeper inspection. This is due to the fact that hadronic mechanics generally implies the mutation of all characteristics of particles, thus including the mutation Q* of conventional charges Q, and we shall write for the mutated charge of the deuteron constituents
where a, b, c are positive-definite parameters, and e is the elementary charge. These mutations are necessary for consistency with other aspects, such as the reconstruction of the exact isospin symmetry in nuclear physics.
However, these mutations are only internal, under the condition of recovering the conventional total charge +e for the system as a whole, as it is the case for closed non-Hamiltonian systems. Consequently, the charge mutations are subject to cancellation in such a way to yield the total charge +e, i.e.,
Needless to say, the mutations of the charge is expected as being quite small in value since, namely as being a second order effect ignorable at a first approximation since the deuteron structure does not require the mutual penetration of the charge distribution of protons.
6.5Fg. Representation of the deuteron spin.
As recalled earlier, quantum mechanics predicts that the most stable state between two particles with spin 1/2 is the singlet, for which the total spin is zero, thus predicting that the ground state of the deuteron as a bound state of a proton and a neutron should have spin zero, contrary to the experimental value of spin 1.
When the deuteron is assumed as being a three-body bound state of two protons with an intermediate electron, hadronic mechanics achieves the exact and invariant representation of the spin 1 of model (6.189) in a way similar to that of the neutron (Section 6.3). It is easy to see that the electron is trapped inside one of the two protons, thus being constrained to have an angular momentum equal to the spin of the proton itself. In this case, with reference to Figure 6.28, the total angular momentum of the isoelectron is null. By recalling that the ground state has null angular momentum, the total angular momentum of the deuteron is given by the sum of the spin 1/2 of the two isoprotons.
Recall that fractional angular momenta are prohibited for quantum mechanics (namely, when angular momenta are defined on a conventional Hilbert space over the conventional field of complex numbers), because they violate the crucial condition of unitarity, with consequential violation of causality, probability laws, and other basic physical axioms.
For hadronic mechanics, the isotopic lifting S* and L* of the spin S and angular momentum L of the electron when immersed within a hyperdense hadronic medium are characterized by
where P and Q are arbitrary (non-null) positive parameters. Recall that Santilli introduced the above isotopy of SU(2)-spin to prevent the believe of the perpetual motion that is inherent when the applicability of quantum mechanics is extended in the core of a star. In fact, quantum mechanics predicts that an electron moves in the core of a star with an angular momentum that is conserved in exactly the same manner as when the same electron orbits around proton in vacuum, thus exiting the boundaries of science, since an electron in the core of a star can only have a locally varying angular momentum and spin as represented by Eqs. (6.194).
For the case of the isoelectron in the deuteron, we have the constraint that the orbital angular momentum must be equal but opposite to that of the spin,
The exact and invariant representation of the spin 1 of the ground state of the deuteron then follows according to the rule
An elaboration of the mechanisms of representing arbitrary angular momenta may be helpful to the non-initiated reader. Suppose that the quantum mechanical angular momentum operator L has expectation value 1,
Under isotopic lifting the above expression easily acquires the value 1/2 for T = 1/2, L* = 2
However, in this case the isounit is given by I* = 1/T = 2. Therefore, when the isoeigenvalue of the angular momentum is properly represented as an isonumber (an ordinary number multiplied by the isounit), one recovers the original value 1,
thus recovering causality and other laws.
Note that there is no violation of Pauli's exclusion principle in this case since that principle only applies to "identical" particles and does not apply to protons and neutrons, as well known (more explicitly, one of the two protons of Eq. (6.189) is in actuality the neutron since it has embedded in its interior the isoelectron).
6.5Fh. Representation of the deuteron magnetic moment.
Recall the first exact and invariant representation of the magnetic moment of the deuteron was reached in Section 5.3 under the conventional proton-neutron interpretation while the proton and the neutron are isoparticles.
We review here Santilli's second, exact and invariant representation of the magnetic moment of the deuteron according to model (6.189). Let us recall the following experimental values of magnetic moments for the deuteron and its constituents
Recall also that the deuteron is in its ground state with null angular momentum in which case there is no orbital contribution to the total magnetic moment from the two protons. By keeping in mind the structure of the deuteron as per Figure 6.28, the exact and invariant representation of the total magnetic moment of the deuteron is then given by
namely, the missing contribution is provided by the total magnetic moment of the isoelectron. In particular, the latter numerical value is given by the difference between the orbital and the intrinsic magnetic moment that is very small (per electron's standard) since the total angular momentum of the isoelectron is indeed small.
Also note the correct value of the sign because the isoelectron has the orbital motion in the direction of the proton spin. But the charge is changed in sign. Therefore, the direction of the orbital magnetic moment of the isoelectron is opposite that of the proton, as represented in Eqs. (6.189). Note finally that the small value of the total magnetic moment of the isoelectron for the case of the deuteron is close to the corresponding value for the neutron, Eqs. (6.132).
6.5Fi. Representation of the deuteron force.
As indicated earlier, the assumption that the deuteron is a bound state of a proton and a neutron permits no identification of the physical origin of the nuclear force. Quantum mechanics merely provides numerous mathematical descriptions of the attractive force via a plethora of potentials, although none of them admits a clear physical explanation of the strong attraction between protons and neutrons.
Santilli's primary objective in generalizing quantum mechanics for nuclear physics is the truncation of this century old failed process of keep adding new and new potentials in the nuclear force, and search instead for fundamentally different notions and representations, a task for which hadronic mechanics has no known equals.
In fact, model (6.189) permits a clear resolution of this additional insufficiency of quantum mechanics via the precise identification of two types of nuclear farces, the first derivable from a Coulomb potential and the second of contact type represented with the isounit.
The constituents in the configuration of Figure 6.28 have short range pair-wise opposite signs of charges and magnetic moments with long range identical signs of charges and magnetic moments. This configuration implies the following net attractive Coulomb force in the deuteron
In addition, the constituents admit an attractive force not derivable from a potential due to the deep penetration of their wavepackets in singlet pair-wise couplings, which force is the same as that of: the two identical electrons in the Cooper and valence pairs (Part III); the structure of mesons (Part IV); the structure of the neutron (Part V); and can be represented via the isounit in now familiar notations
As the reader may recall from Sections 6.2 and 6.3, the projection of the above force in our spacetime (that with trivial unit 1) characterizes a strongly attractive Hulthen potential, that behaves at short distances like the Coulomb potential, by therefore "absorbing" the latter and resulting in a single, dominating, attractive Hulthen well with great simplification of the calculations.
Besides the above potential and contact force, no additional nuclear force is needed for an exact and invariant representation of the remaining characteristics of the deuteron (such as binding and total energies), as shown below.
For instance, the mysterious " exchange force potentials" (in which protons and neutrons interchange themselves) become unnecessary and, if used, misleading because the underlying physical effect is of purely contact type, thus having no meaningful potential at all. If a potential is granted, as done throughout the 20th century, it is like describing the resistive force of a spaceship during re-entry in our atmosphere with a potential, thus exiting the boundary of science.
It is easy to prove that the isoelectron cannot solely be restricted to exist within one of the two protons, because there exists a 50% isoprobability of moving from the interior of one proton to that of the other proton. Therefore, the proton-neutron exchange is confirmed by model (6.189) and so is the attractive character of the related force.
Similarly, "noncentral forces" are un-necessary in model (6.189) because they become a particular case of the broader nonlocal forces extended over the volume of wave-overlappings. The important point is that, again, noncentral forces generally do not have a potential energy in classical mechanics and the idea that they could instead acquire a potential energy in nuclear mechanics is not plausible unless proved beyond doubt.
A similar fate holds for the various other mysterious forces adopted in nuclear physics during the 20th century. They all become un-necessary for the treatment via hadronic mechanics unless their action-at-a-distance, potential character is established on rigorous grounds.
An illustration is that of "velocity-dependent potentials." They are known as being particular cases of contact nonlocal forces because the latter are approximated via power series in the velocities and other variables.
The occurrence illustrates again the remarkable power of the isounit for unifying a considerable variety of forces assumed as being of potential type in the 20-th century, with a consequential dramatic reduction of the number of meaningful nuclear forces.
6.5Fj. Representation of the deuteron total energy.
As it is well known, the binding energy of the deuteron is given by
Recall from the main lines of hadronic mechanics that the binding energy is mainly characterized by forces derivable from a potential since the contact forces due to mutual wave-overlapping of wave packets have no potential energy. Hence, the binding energy of the deuteron is due to the potential component of the deuteron binding force, Eq. (6.202), as the reader can verify by using known values of charges and magnetic moments for the two electron-proton pairs of the deuteron and their mutual distances as identified earlier.
Hadronic mechanics also permits the exact and invariant representation of the total energy of the deuteron, that, as such, becomes another verification of model (6.189). Recall the following conversion of one atomic mass unit to MeV
and the known values
The mass of a nucleus with A nucleons and Z protons without the peripheral atomic electrons is characterized by
that yields for the deuteron
The iso-Schroedinger equation for model (6.189) can be reduced to that of the neutron, Eq. (6.103), under the assumption that the isoelectron spends 50% of the time within one proton and 50% within the other, thus reducing model (6.189) in first approximation to a two-body system of two identical particles with un-isorenormalized mass M* = 937.782 MeV, the main differences being given by different numerical values for the energy, meanlife and charge radius.
Santilli reaches in this way the structure equation of the deuteron in a first two-body nonrelativistic approximation
It is easy to see that the above equations admit a consistent solution reducible to the algebraic expressions as for the case of Rutherford-Santilli neutron
it should be indicated that, in the above model, the deuteron binding energy is null,
because all potential contributions have been included in the structure of p* and, for the binding of the two p*, all potential forces have been "absorbed" by the nonlocal forces and k2 has now reached the limit value of 1 (while being close to but bigger than 1).
A more accurate description can be obtained via the restricted three-body configuration of Figure 6.28 that, as such, also admits an exact solution. The model can be constructed via a nonunitary transform of the conventional restricted three-body Schroedinger equation for two protons with parallel spin 1/2 and one isoelectron with null total angular momentum as per Figure 6.28 with conventional Hamiltonian H = T + VCoul, where VCoul is expression (6.202). The nonunitary transforms then produces an additional strong Hulthen potential that can, again, "absorb" the Coulomb potential resulting in a solvable equation. This more accurate approach is left to the interested researcher.
6.5Fk. Representation of the deuteron electric dipole moment and parity.
The electric dipole moment of the deuteron is identically null. Its representation via hadronic mechanics follows from the fact that isotopies cannot alter null values.
The positive parity of the deuteron is trivially represented by hadronic mechanics via the expression
and the value for the unperturbed deuteron in its ground state L* = L = 0.
By comparison, the reader should be aware of another misrepresentation existing in the nuclear literature consisting of the fact that, on one hand, the parity of the deuteron is positive (L = 0), while on the other hand, in order to attempt a recombination of deuteron magnetic moments and spin, the unperturbed deuteron is assumed as being a mixture of different levels, some of which have non-null values of L, thus implying the impossibility of a positive parity.
In summary, Santilli has shown that the isotopic branch of nonrelativistic hadronic mechanics permits the exact and invariant representation of "all" the characteristics of the deuteron composed by two isoprotons and one isoelectrons, while jointly resolving all quantum insufficiencies identified above.
6.6. Reduction of matter to proton and electrons.
It is evident that, following the reduction of the neutron to a proton and an electron and the reduction of the deuteron to two protons and one electron, Santilli has indeed achieved the important reduction of all matter to protons and electrons, since the reduction of the remaining nuclei to protons and electron is consequential, e.g., as a hadronic bound state of two mutated deuterons.
6.7. Reduction of neutron stars to protons and electrons.
We have pointed out earlier various astrophysical implications off Santilli's research, such as:
1) The initiation of antimatter astrophysics with the first known possibility of identifying whether a far away star or galaxy is made up of matter or of antimatter (Section 3.7);
2) The absence of universe expansion, big bang, dark matter and dark energy expected from Santilli isoredshift (Section 5.5);
3) The new conception of stars as a portal for continuous creation via the transfer of energy from the universal substratum to out world as needed for the synthesis of the neutron (Section 6.2) and other astrophysical contributions.

Figure 6.29. Artist rendering of a neutron star.
We would like to close this chapter by indicating Santilli's additional astrophysical contribution given by the fact that the so-called "neutron stars" are in reality an extremely high density and high temperature fluid composed by the original constituents of the star, protons and electrons, in conditions of deep mutual penetration under the laws of hadronic mechanics.