NEW SCIENCES FOR A NEW ERA:
Mathematical, Physical and Chemical Discoveries of
Ruggero Maria Santilli
I. Gandzha and J Kadeisvili
PRINTED VERSION
I. Gandzha and J Kadeisvili, New Sciences for a New Era:
Mathematical, Physical and Chemical Discoveries of
Ruggero Maria Santilli,
Sankata Printing Press, University of Kathmandy, Nepal (2011),
Free pdf download
http://www.santilli-foundation.org/docs/RMS.pdf
CHAPTER 3:
DISCOVERIES IN PHYSICS
3.1. FOREWORD
3.2. ETHER AS A UNIVERSAL SUBSTRATUM (1952-1955)
3.3. ORIGIN OF THE ELECTRIC AND MAGNETIC FIELDS (1955-1957)
3.4. ORIGIN OF THE GRAVITATIONAL FIELD (1974)
3.5. SYMMETRY OF THE ETHER (1970)
3.6. QFT (AND QCD) VIOLATIONS FROM DISCRETE SYMMETRY VIOLATIONS (1974)
3.7. RESOLUTION OF THE HISTORICAL IMBALANCE ON ANTIMATTER (1994)
3.7A. Foreword
3.7B. Newton-Santilli isodual equation for antimatter
3.7C. Isodual representation of the Coulomb force
3.7D. Hamilton-Santilli isodual mechanics
3.7E. Isodual special and general relativities
3.7F. Prediction of antigravity
3.7G. Test of antigravity
3.7H. Isodual quantum mechanics
3.7I. Experimental detection of antimatter galaxies
3.7J. The new isoselfdual invariance of Dirac's equation
3.7K. Dunning-Davies thermodynamics for antimatter
3.7L. Isoselfdual spacetime machine
3.7M. Original literature
3.8. INITIATION OF q-DEFORMATIONS OF LIE THEORY
3.9. THEOREMS OF CATASTROPHIC INCONSISTENCIES OF
NONCANONICAL AND NONUNITARY THEORIES
3.9A. The majestic consistency of Hamiltonian theories.
3.9B. Theorems of catastrophic inconsistencies of noncanonical and nonunitary theories.
3.9C. Examples of catastrophically inconsistent theories.
3.10. SANTILLI RELATIVITIES (1978)
3.10A. Historical notes
3.10B. Santilli's opening statement
3.10C. Conceptual foundations
3.10D. Mathematical foundations
3.10E. Invariance and universality of Santilli's isotopies.
3.10F. Lorentz-Poincare'-Santilli isosymmetry and its isodual
3.10G. Santilli's isorelativity and its isodual
3.10H. Santilli's isogravitation and its isodual
3.10I. Santilli's geno- and hyper-relativities and their isoduals
3.10J. Isotopic reconstruction of exact spacetime symmetries when conventionally broken
3.10K. Experimental verifications
3.10L. Original literature
3.11. HADRONIC MECHANICS (1967)
3.11A. Foreword
3.11B. Historical notes
3.11C. Interior and exterior dynamical systems
3.11D. Closed and open dynamical systems
3.11E. Newton-Santilli isoequations
3.11F. Hamilton-Santilli isomechanics
3.11G. Animalu-Santilli isoquantization
3.11H. Hilbert-Santilli isospaces
3.11I. Schroedinger-Santilli isoequations
3.11J. Heisenberg-Santilli isoequations
3.11K. Elimination of quantum divergencies
3.11L. Genotopic and hyperstructural branches of hadronic mechanics
3.11M. Isodual branches of hadronic mechanics
3.11N. Two-body hadronic system
3.11O. Simple construction of hadronic mechanics
3.11P. Invariance of hadronic mechanics
3.11Q. Relativistic hadronic mechanics
3.11R. Direct universality and uniqueness of hadronic mechanics
3.11S. EPR completion of quantum mechanics, hidden variables and all that
3.11T. Operator isogravity
3.11U. Iso-grand-unification
CHAPTER 3:
SANTILLI'S DISCOVERIES IN THEORETICAL PHYSICS
3.1. FOREWORD
In this chapter, we outline Santilli's most important discoveries in physics and provide copies of the original papers in free pdf downloads, when copyrighted. As it was the case for Chapter 2, we regret not to be able to outline subsequent contributions by independent researchers to avoid a prohibitive length, but they can be located in the
General Bibliography on Santilli Discoveries
The serious scholar is suggested not to restrict the attention solely to individual topics, but provide primary attention to the overall mathematical and physical construction with particular reference to its consistency as well as beauty.
None of the discoveries presented in this chapter has been disproved in the scientific literature to our best knowledge. Scholars are requested to inform the Foundation of the existence of papers in the refereed journal disproving any of the discoveries listed in this chapter for their outline, quotation and listing in the related section.
During the first subsections, we shall use for clarity the conventional associative multiplication AB of numbers, vector fields, operators, etc., and use the symbol AxB for the same multiplication when initiating the presentation of classical or operator generalized theories.
3.2. ETHER AS A UNIVERSAL SUBSTRATUM (1952-1955)
Santilli was fascinated by the ether (also called aether, or space) since his high school studies in the 1950 that he conducted in the city of Agnone, province of Isernia, Italy. A controversy was raging at that time on space conceived as a universal medium (or substratum) because such as conception was believed to be in conflict with special relativity due to its foundation on the lack of existence of a privileged reference frame.
An argument used to deny the existence of space as a universal medium was the lack of "aethereal wind," namely, the absence of any resistance by Earth during its motion in space. Another argument was the use of Einstein's photon for the reduction of light to particles, thus eliminating the need for a medium to propagate electromagnetic waves.
In his first writings dating back to his high school years, Santilli opposed these views. To begin, he saw no conflict between the existence of a universal medium and special relativity because, assuming that an absolute reference frame can be set at rest with said universal medium, that frame cannot be identified by man precisely in view of the relativity of motion.
In 1952, when 16 years old, Santilli delivered a seminar on Albert Einstein to the teachers and students of his high school whose transcript (in Italian) has been retrieved by our Foundation from the high school documents and made available in free pdf download:
"Albert Einstein"
Seminar delivered by R. M. Santilli in 1952 at the High School in Agnone (Isernia), Italy.
Next, Santilli accepted the reduction of light to photons, but only for high frequencies, such as for UV or gamma rays, and rejected the reduction to photon for electromagnetic waves at large, such as those with large wavelength (e.g., radiowaves), thus considering the notion of photon as an approximation of reality motivated by the characteristics of electromagnetic waves to cause an impulse when hitting a surface, since they carry energy. As a general position, he writes (in Italian): My voice can be heard because there is air as a medium propagating sound waves and, in the absence of air, no voice can be propagated. By the same token, my face can be seen because there is a universal medium to propagate light and, again, in the absence of a universal medium, light could not exist or propagate.
By noting that sound waves are longitudinal because the medium (air) is compressible, and by noting that electromagnetic waves are transversal, Santilli assumed that space is a universal medium with very high rigidity and, consequently, very high energy density, (otherwise light would be characterized by longitudinal or other forms of waves).
Finally, Santilli dismissed the hypothesis of the "aethereal wind" because he conceived space as the universal substratum necessary for the characterization not only of electromagnetic waves, but also of the elementary particles constituting matter, the difference being that oscillations of space propagate in the former case in the form of waves, while they are stationary in the latter case (unless moved).
In particular, Santilli assumed the electron to be a pure oscillation of space, that is, the electron is characterized by an oscillation of a point of space without any oscillating "little mass" or any other material entity, and assumed the same for all other particles constituting matter, although with a much more complex oscillating structure. In this way, Santilli eliminates the "aethereal wind" by writing:
As we shall see, Santilli returned to his conception of space some 50 years later following his discovery of new mathematics permitting quantitative studies of the expected interconnection between space as a universal medium with high energy density and matter (achieved via the isotopies of Hilbert spaces and fields at the foundation of hadronic mechanics). In particular, his conception of space emerged rather forcefully in his studies on: the synthesis of the neutron and the expected continuous creation in our universe; alternatives to the neutrino conjecture via longitudinal impulses propagating through space; geometric propulsions with unlimited speeds without fuel tanks; and other far reaching conceptions.
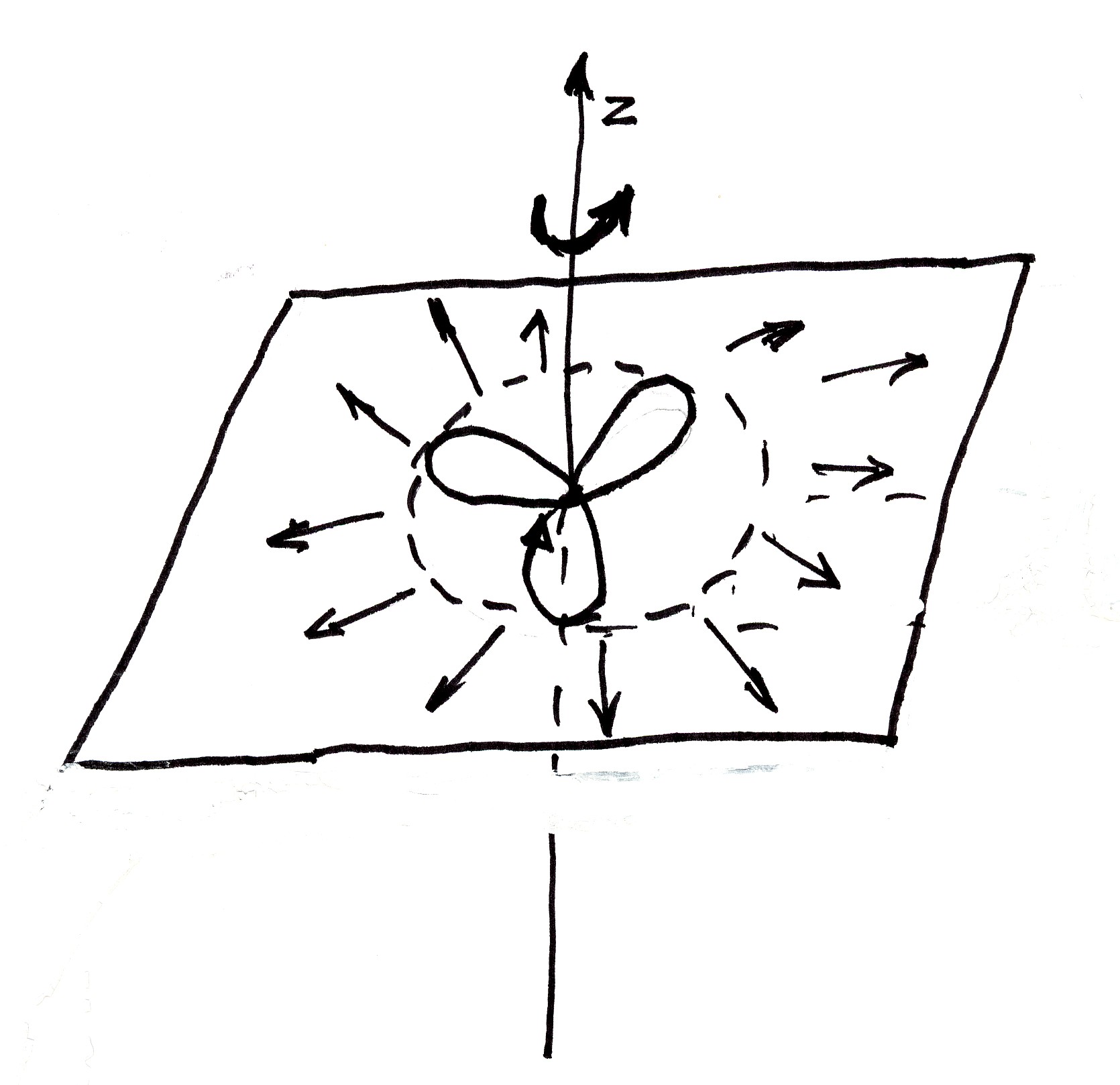
Figure 3.1. An original drawing by Santilli dating back to 1955 on his conception of the structure of the electron as a pure oscillation of a point of the ether, showing the distribution on a plane due to rotation, the longitudinal force propagated through space, thus being interpreted as the origin of the electric charge, Eq. (3.2).
Santilli's conception of the ether
The elements indicated above refer to studies in the 1950s. The understanding of Santilli's conception of space requires the knowledge of all his studies, including experimental verifications and applications.
To begin, there is the need of a technical knowledge of Santilli's representation via hadronic mechanics of the synthesis of the neutron from a proton and an electron as occurring in Stars that requires 0.782 MeV (see Chapter 5). The only plausible origin of the missing energy is the ether because, in its absence, stars could never initiate to produce light. In fact, even a small star synthesizes at its initiation about 1030 neutrons per seconds, thus requiring about 1030 MeV that, unless supplied by the ether, would prevent any additional nuclear syntheses. This leads to the conception of the ether as a universal medium with extremely high density of positive energy, as indicated above.
But the universe is expected to be symmetric under charge conjugation. Therefore, the synthesis of the antineutron from antiprotons and antielectrons requires, this time, 0.782 MeV of negative energy (referred to a negative unit as per the isodual theory of antimatter) that, again, can solely be obtained from the ether. This leads to the additional conception that the ether is also constituted by a very large density of negative energy.
The understanding of the coexistence of the positive and negative energies in the ether requires a technical knowledge of Santilli's hypergeometries. In essence, positive and negative energies can coexist because defined in different spaces characterized by different units, the positive unit for positive energy and the negative unit for negative energy (two-valued hypergeometry). The conventional (classical) notion of vacuum originates precisely from the superposition of opposite energies defined in different spaces.
The above conception of the ether appears to be confirmed by serious studies of all existing physical knowledge from particle physics to astrophysics, such as pair creation in particle physics, neutron and antineutron stars in astrophysics, etc. The expectation is that the scholar is sufficiently serious to study Santilli's results before throwing judgments solely based on the old and surpassed knowledge of the 20th century.
Original literature
Our Foundation has identified some (but not all) original writings by Santilli and we make them available here as free pdf downloads for interested scholars. We list the first book written by Santilli in 1955 (but not listed in his CV) and two articles of 1955 and 1956. Note the title of the second article (Elimination of the mass in atomic physics) that anticipate the need to replace the mass with energy in Newton's and Einstein's gravitation discovered years later and outlined below.
"Principi su una Teoria Unificata sulla Fisica Atomica" (Principles for a Unified Theory in Atomic Physics)
R. M. Santilli,
Naples (1955)
"Eliminazione della massa nella fisica atomica" (Elimination of mass in atomic physics),
R. M. Santilli, Phoenix, Volume 1, pages 222-227 (1955)
Perche' lo spazio e' rigido (Why space is rigid)
R. M. Santilli,
Il Pungolo verde, Campobasso, Italy, (1956)
The Foundation is interested in providing financial support to studies on the ether as a universal substratum, under the conditions that the assumed characteristics of the ether allow a quantitative representation of the transversal character of light, as done by Santilli with his rigidity equivalence of the ether, thus excluding models of the ether as being a fluid and the like.
3.3. ORIGIN OF THE ELECTRIC AND MAGNETIC FIELDS (1955-1957)
As a natural continuation of the preceding conception of the ether, Santilli concentrated his attention in the structure of the electron as part of his 1957 thesis for the degree in physics at the University of Naples, Italy.
Starting from the compelling need for space to be a universal medium with high rigidity to characterize light via transversal waves propagating at very high speed, and the consequential need for the electron to be a pure oscillation of space in the sense indicated above, Santilli addressed the problem of the origin of the elementary charge and magnetic field or, equivalently, the structure of the electron.
In recollection of these studies, he states: I believe that no study on the electron can be claimed to be of structural character unless it explains how it is possible for one electron to exercise an attractive force with a positron and a repulsive force with another electron. The conjecture I studied in the 1950s is the logical consequence that each electron (or positron) releases both attractive and repulsive forces through space, which forces are then separated by the coupling with another elementary charge.
His main intuition is that the electron is widely represented with its well known characteristic frequency
Hence, he argued that the elementary charge "e" cannot possibly be a constant as believed during the 20th century, but must also show some form of periodic time dependence. The understanding is that a collection of sufficient number of elementary charges q = ∑k ek is indeed expected to be constant as per known experimental evidence.
The issue raised by the characteristic frequency (3,1) is the following: If space is a universal medium with high rigidity, the oscillation of one of its points will propagate an oscillating force in the medium that can be safely assumed to decay with the inverse square of the distance. However, when such a force encounters another electron (positron), it results in a repulsive (attractive) force.
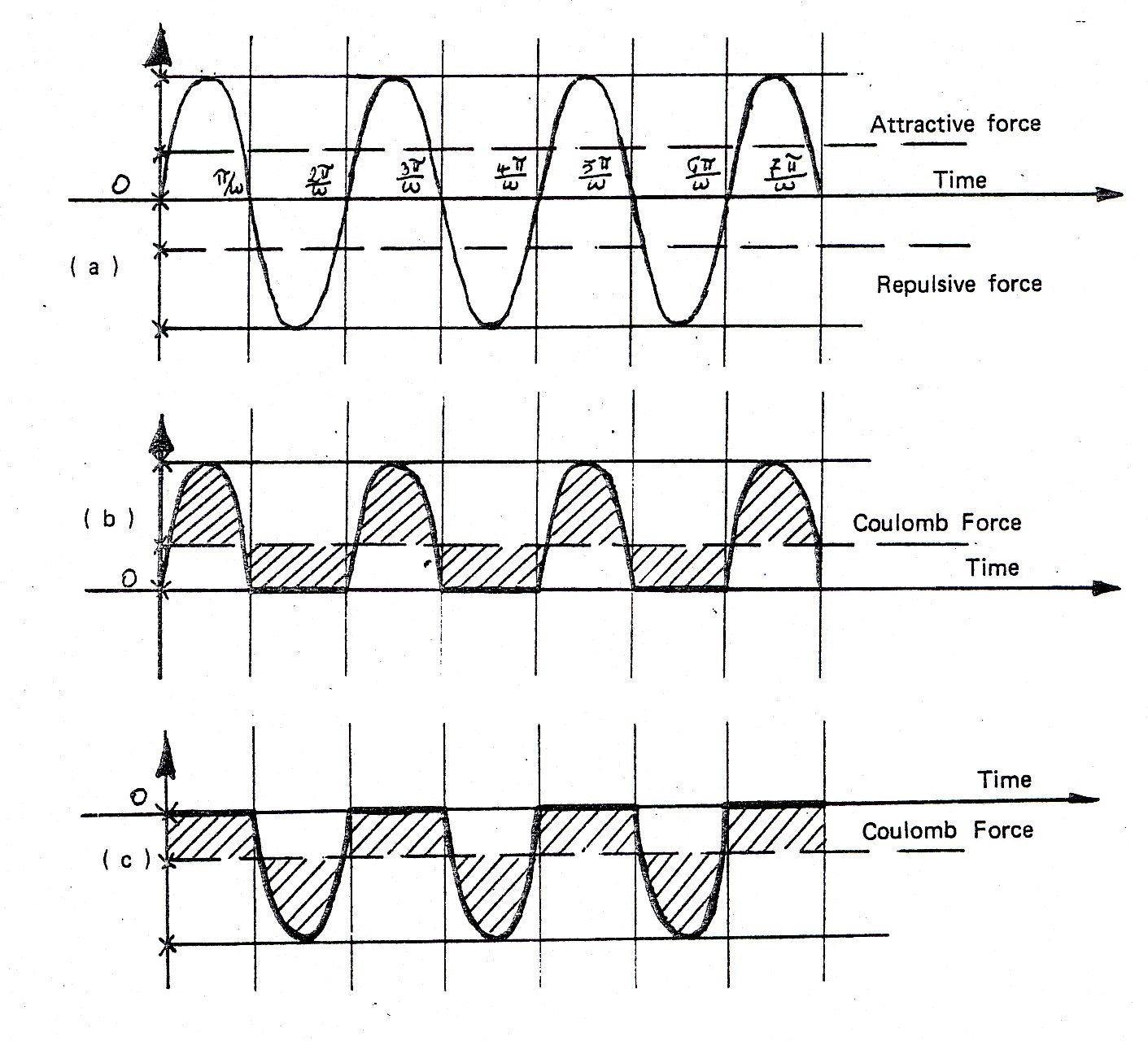
Figure 3.2. Another original drawing by Santilli dating back to 1955 on his conception of the elementary charge of the electron according to Eq. (3.2) as containing both attractive and repulsive actions (top view), which actions are separated into repulsive or attractive force when coupling elementary charges of the same or opposite sign, respectively (lower views).
The solution identified by Santilli is that the coupling of identical elementary charges activates only the repulsive part of the oscillating force, while the coupling of opposing charges activates only the attractive component of the oscillating force propagating through space.
Hence, Santilli assumed that such an oscillation transfers to space an oscillating force with the same frequency, resulting in the following structure model of the elementary electric charge
In this way Santilli reached in 1955 a structural generalization of the Coulomb law for two elementary charges into a time dependent, pulsating form that, for the simplest possible case of two one-dimensional oscillations along the same axis can be written
where the positive (negative) sign denotes repulsion (attraction) and R is the amplitude of the oscillation, with much more complex expressions for oscillations in two and three dimensions (see for details the literature quoted below). Needless to say, the actual model contains a complex phase terms in the argument of the sinus that is a function of the rotation or, equivalently, of spin 1/2 of the electron, we cannot review here.
Santilli then concluded with the hypothesis that The repulsive force between two identical electrons is not constant, but has the shape of half a sinusoid with the characteristic frequency of the electron. It should be indicated again that the above hypothesis solely applies for two electrons because, when considering a large number of electrons, the above periodicity is evidently averaged out, resulting into a constant force.
The conception of the electron as a pure oscillation of space is far from being trivial and should be taken seriously by researchers in the field, if nothing else, because alternative hypotheses appears to lack plausibility. In fact, the addition of rotation to the pure oscillation of space creates a rosetta-type planar distribution with an SO(2) symmetry that (unlike the SO(3) case) admits angular momentum 1/2 as the lowest non-null state, thus allowing a structure model of the electron spin.
Additionally, an oscillation of a point of a rigid medium propagates two different impulses in the medium, the radial one identified with the origin of the electric charge, and the transversal one that propagates in the two directions opposite to the oscillation thus having all prerequisites for their interpretation as the origin of the elementary magnetic dipole moment, as illustrated in the figure.
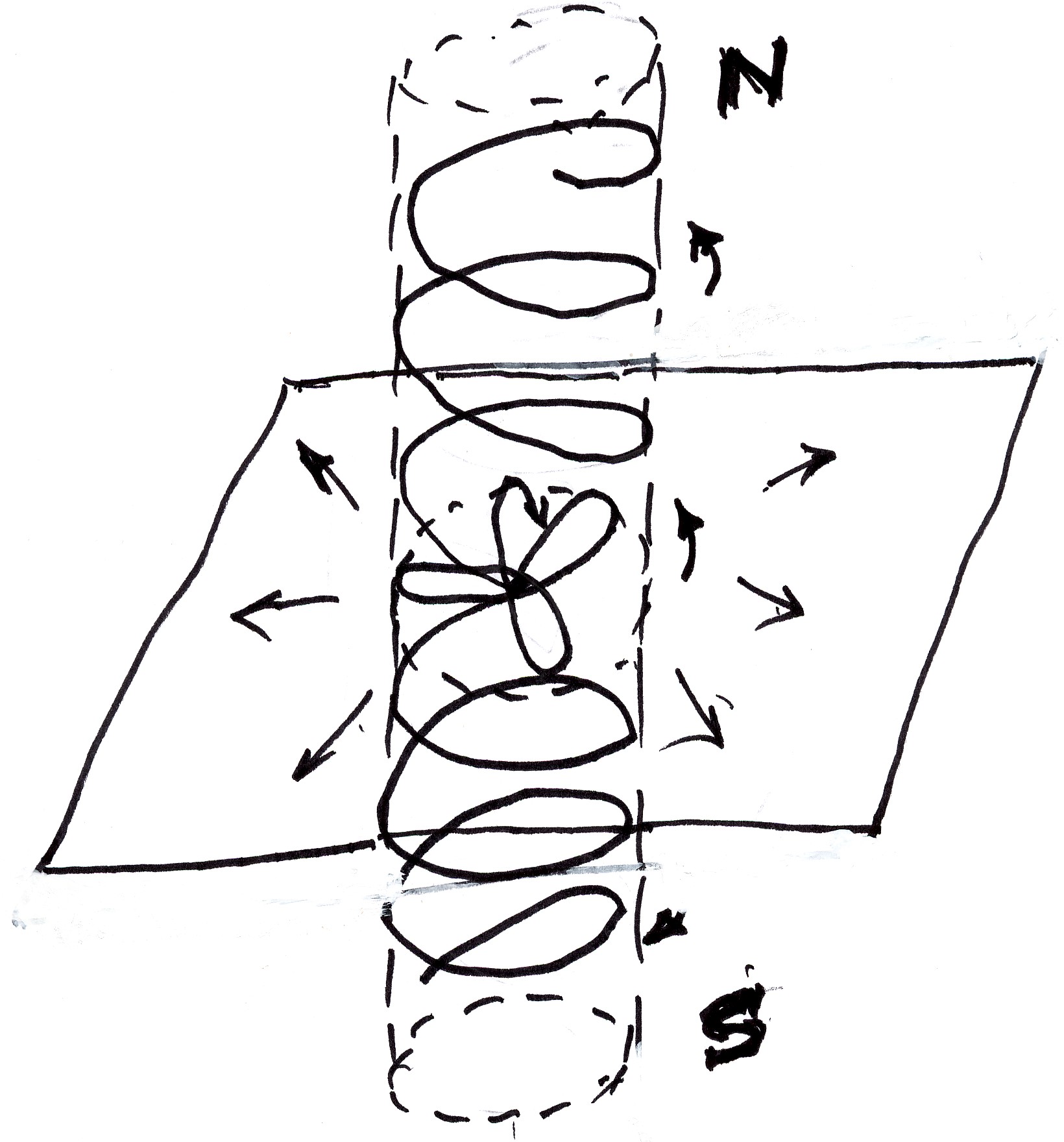
Figure 3.3. An original drawing by Santilli dating back to 1955 on his conception of the origin of the magnetic field of the electron conceived as a pure oscillation of space, showing the clear duality of the field along the rotational symmetry axis originating from deformations of space perpendicular to the characteristic structural oscillation.
Half a century has passed since these pioneering studies and, in view of the obscurantism created by Einsteinian theories, studies on space as a universal substratum have been vastly ignored by the so-called "mainstream" of physics research, with the consequential dismissal of studies on the origin of the electromagnetic field in favor of its description.
Yet, Santilli must be credited to have voiced a restoration of serious scientific democracy with the addressing of truly fundamental physical issues irrespective of their political implications, a pattern that has been at the basis of Santilli's entire life.
Our Foundation has retrieved Santilli's thesis (in Italian) at the University of Naples on the structure of the electron and the origin of its electromagnetic field, and makes it available in free pdf download:
"Fondamenti per una teoria unificata sulla struttura dell'elettrone" (Foundations for a unified theory on the structure of the electron)
R. M. Santilli,
Department of Nuclear Physics. University of Naples (1958)
Following various academic research, Santilli resumned a study of the above ideas only in the early 1980s, and released two short papers for publication in the Hadronic Journal and in Nuovo Cimento Letters merely to have a (generally ignored) record of his studies
A structure model of the elementary charge
R. M. Santilli, Hadronic J. Vol. 4, 770-784 (1981)
A conceivable lattice structure of the Coulomb law
R. M. Santilli, Lettere Nuovo Cimento Vol. 37, 505-508 (1983)
The connection between Santilli's structure model of the electron and string theories (appeared some half a century later) should be noted. Unfortunately, the latter have been patterned along the requirement of representing extended particles while verifying special relativity, a notorious impossibility since the latter solely admit point-particles as indicated earlier.
In Santilli's views, string theories essentially constitute an edifice built without foundations due to the lack of identification of the truly fundamental notion, the entity that vibrates thus permitting the existence of the strings. This identification is generally omitted because the universal substratum would be perceived as violating special relativity. Additionally, string theories in their current formulation verify the Theorems of Catastrophic Mathematical and Physical Inconsistencies of Noncanonical and Nonunitary Theories reviewed in Section 3.9. Due to these unsettled aspects, string theories will be ignored hereon.
Yet, it is clear that Santilli's structure model of the electron can indeed provide a plausible foundation to string theories, and their reconstruction based on a universal substratum and related advances is here recommended.
The Foundation is interested in providing financial support for the experimental verification or denial of Santilli's laws (3.2) and (3.3) and is seeking interested experts in the field.
3.4. ORIGIN OF THE GRAVITATIONAL FIELD (1974)
Following the above pioneering studies on th structure of space and the origin of the electromagnetic field, it was natural for Santilli to study the origin of the gravitational field. This study was conducted in the 1970s when he was at the Center for Theoretical Physics of the Massachusetts Institute of technology.
Santilli initiated the study with the origin of the exterior gravitational field for the most elementary particle, the electron, whose mass is well known to be entirely of electromagnetic origin. Hence, he reached the conclusion that the gravitational field of an electron is entirely of electromagnetic origin, and wrote the gravitational field equations on a Riemannian space in the form
where T
The above case is well known but ignored in the sense that, when passing to neutral matter, it is customary to assume that mass is the origin of the gravitational field. Therefore, Santilli studied the exterior gravitational field of the πo particle as a bound state of one charged constituent called "parton" and its antiparticle (assumed to have the same elementary structure of the electron). The constituents were assumed to be in very high rotation at 1 fm mutual distance with tangential speeds close to that of light. By using the most advanced relativistic calculations, Santilli discovered that the mass of the πo is also of entire electromagnetic origin. Therefore, for the gravitational field of the πo Santilli wrote the field equation in the form (3.4), namely, with a first order source tensor in the r.h.s.
He then passed to the study of ordinary massive bodies and reached the conclusion that the exterior gravitational field in vacuum of an ordinary massive body is entirely generated by the sum of the electromagnetic fields of all elementary constituents of the body considered, with field equations of type (3.4) having a source tensor in the r.h.s. of first order in magnitude, irrespective of whether the body considered is neutral or charged and with or without a magnetic field. In this case, Santilli characterized the source tensor T
He then passed to the problem of the origin of the interior gravitational field by recalling that, from a structural viewpoint, the main difference between the exterior and the interior problem is the additional presence in the interior case of short range, weak and strong interactions. Hence, for the interior gravitational problem of the πo particle, he wrote the field equations in the form
Santilli also noted that: the tensor Tμ ν is traceless, while the tensor Wμ ν is not; the source tensor of the interior problem has a bigger numerical value of that for the exterior problem; and, consequently, he concluded that the inertial mass is bigger than the gravitational one, the former (latter) being characterized by the interior (exterior) problems.
Santilli then compared the above results (reached via first principles of quantum electrodynamics) with Einstein's conception of the exterior gravitational problem that, as well known, is based on its entire reduction to curvature without any source for neutral bodies, and celebrated field equations
A) One assumes Einstein gravitation as being correct, in which case classical and quantum electrodynamics must be profoundly reformulated in such a way to avoid a first order electromagnetic contribution to masses; or
B) One assumes quantum electrodynamics as being valid, in which case Einstein's reduction of gravity to pure curvature without source (for the case of neutral bodies) must be abandoned.
Santilli then concluded the study of 1974 with its evident consequence: The electromagnetic origin of the gravitational fields implies their "identification," thus eliminating the need for their "unification", with the understanding that the former (latter) field is described by second-order (first-order) equations.
In the late 1990s, Santilli added the proof that Einstein's field equations for a neutral body are additionally incompatible with the Feud identity of the Riemannian geometry, since the latter requires two source tensors in the r.h.s of the field equations, one traceless and the other with trace, exactly as predicted by the origin of the interior gravitational field, Eqs. (3.5). Santilli also identified numerous additional inconsistencies of Einstein's gravitation reviewed later on in this chapter.
The implications of the above studies are far reaching, even though vastly ignored for evident political reasons of not being aligned with Einsteinian doctrines. In fact, Santilli's identification of the gravitational and electromagnetic fields implies:
A) The evident equivalence of phenomenologies, that is, gravity must admit attraction and repulsion since that is the case for the electromagnetic field. This problem was resolved by Santilli via the construction of the isodual theory of antimatter (see later on Secton 3.19);
B) The possibility of resolving the century old unresolved problem of a consistent operator form of gravity, that was subsequently achieved by Santilli via his isogravity (see Section 3.11);
C) The need to formulate the scattering theory in such a way to incorporate, apparently for the first time, gravitational contributions, due to the possible creation of ,Mini Black Holes since the latter depend on sufficient energy density, and not necessarily occur solely for large masses (see Chapter 5).
The origin of the gravitational field and its identification with the electromagnetic field were published by Santilli in the paper:
Partons and gravitation: some puzzling questions
The violation by Einstein's gravitation of the Freud identity of the Riemannian geometry for neutral bodies and nine inconsistency theorems were presented in the paper
Nine theorems of catastrophic inconsistencies of general relativity and their possible resolution via isogravitation
with a general review in the volume
Hadronic Mathematics, Mechanics and Chemistry, Volume I: Limitations of Einstein's Special and General Relativities,
Quantum Mechanics and Quantum Chemistry
3.5. SYMMETRY OF THE ETHER (1970)
As indicated earlier, Santilli considers the ether (or space) to be a universal substratum permitting the existence of all visible universe, thus being the most fundamental and final frontier of scientific knowledge. The physics community of the 20th century did not accept this notion because it implies an absolute reference frame that is perceived as being prohibited by special relativity, thus adapting nature to a preferred theory.
Being a physicist interested in quantitative studies, it was natural for Santilli to search for the symmetry of the ether, that is, the spacetime symmetry admitting indeed a universal substratum for all visible events, while, of course, being compatible with available experimental evidence. The absence of such a symmetry originates from the fact that there is no possibility to characterize said notion of the ether via the spacetime symmetry of the 20th century, the 10-dimensional Poincare' symmetry, here indicated in its simpler connected form
Hence, Santilli searched for a broadening of the Poincare' symmetry in such a way to admit special relativity as a particular case, while allowing means for the characterization of the ether via a primitive, spacetime symmetry.
The solution was presented in a series of papers written from 1970 on by Santilli in collaboration with P. Roman and J. J. Aghassi at the Department of Physics of Boston University. The proposal consisted in the 15-dimensional ether symmetry as called privately by Santilli and officially called in publications the relativistic Galilei group G5(3+2) where 5 denotes the extension of the 4-dimensional Minkowski spacetime with coordinates xμ, μ = 1, 2, 3, 4, plus an additional scalar u characterizing the ether as a universal medium, e.g., u representing the ether proper time. The new symmetry is characterized by the transformations
In summary, the Poincare' symmetry can be extended into the ether symmetry (or the relativistic Galilei symmetry) G5(3, 2) that admits as a subgroup both the Poincare' symmetry and the conventional (nonrelativistic) Galilei symmetry, as well as fundamental new features that are impossible in the Poincare' symmetry, such as the position and energy operators, a universal constant (originating from the scalar extension) and other intriguing features.
A possible use of the ether symmetry is the following. The Poincare' component is used for the representation of all data connected to special relativity with no change, including the adoption of all its experimental verifications. The remaining components mainly represent the interplay between cosmological aspects, the universal medium, and the event considered. The latter cause the emergence of position and energy operators that are an evident consequence of the introduction of the proper time of the ether.
Needless to say, it would be presumptuous to claim that the ether symmetry is the correct spacetime symmetry for relativistic dynamics, and the same holds for the believe of the Poincare' symmetry as the final spacetime symmetry to the end of time. Yet, it is the Foundation's opinion that, until experimental evidence disproving the new symmetry is identified, the ether symmetry is superior to the Poincare' symmetry, if nothing else, because of the much broader conception and representational capability.
The two papers below are the historical paper presenting the new spacetime symmetry. For numerous additional papers, particularly those on the representation theory and applications, interested scholars are suggested to consult Santilli curriculum.
A new dynamical group for the relativistic quantum
mechanics of elementary particles
Representation theory of a new relativistic dynamical group
An important study of the nonrelativistic case has been done by H. E. Wilhelm in the paper
Galilei invariant electrodynamics and quantum mechanics relative to the cosmic aether frame
An important independent study has been made by J. R. Fanchi in the recent memoir
Tutorials on parametrized relativistic dynamics
The reader should be aware that the American Physical Society
prohibited any mention of the use intended by Santilli of the relativistic
Galilei symmetry for the characterization of a universal substratum,
for the evident political reason to avoid the perception of the
paper being incompatible with Einsteinian doctrines. The
presentation of the new symmetry adopted above has been derived by
the Foundation from Santilli's unpublished manuscripts of the time,
and coincides with the above quoted Phys. Rev. paper only in the
formulae.
3.6. QFT (AND QCD) VIOLATIONS FROM DISCRETE SYMMETRY VIOLATIONS (1974)
The rigorous implementation of Lie's theory demands that the fundamental symmetry of special relativity, the Poincare' symmetry, is given by a continuous component characterized by the (connected) Lorentz symmetry, and discrete components characterized by space and time inversions.
In the early part of the 20th century, the entire Poincare' symmetry was assumed to be exactly valid throughout the universe. The discovery of parity violation by weak interactions, rather than causing scientific joy, caused panic among the Einsteinian followers because of fear that the entire edifice may collapse. Organized interests on a world wide basis were then activated in the physics community to reach a vast consensus, intentionally without any technical inspection, that "the violation of discrete symmetries does not cause the violation of the continuous component of the Poincare' symmetry or of special relativity," a popular political belief without scientific process that is still widespread at this writing (mid 2008).
Thanks to his notorious independence of thought from popular, academic beliefs, Santilli conducted in the 1970s quantitative technical studies as to whether the violation of discrete symmetries implies that of the connected Lorentz symmetry and, consequently, of special relativity. The analysis was conducted with the most advanced and rigorous technical knowledge in quantum field theory of the time, that via Wightman's axioms.
Being an applied mathematician, Santilli was fascinated by the beauty of quantum field theory (QFT) characterized by Whitman axioms. However, being a physicist, he also knew that such a theory had to admit limits of exact applicability because physics will never admit final theories to the end of time. Thus, he initiated comprehensive studies for the identification of such limits of applicability as a necessary foundation for suitable covering theories. The reader should be aware that these studies are of extreme complexity and, therefore, can be only reviewed here in their main conceptual lines.
The discrete symmetries of quantum field theories are given by the following operations and their combinations:
While supervising a Ph. D. thesis of one of his students at the Department of Physics of Boston University (the Greek physicist C. N. Ktorides), Santilli achieved the extension of the PCT theorem to all discrete spacetime symmetries, a possibility simply unknown at that time. To achieve this goal, he derived the following dual discrete symmetries
:
THEOREM 3.6A: Under Lorentz invariance, analyticity and energy boundedness from below, the validity (at a Jost point) of any discrete symmetry in a quantum field theory satisfying the Whitman axioms implies that of its dual and vice versa:
Generalization of the PCT theorem to all discrete spacetime symmetries in quantum field theory,
The reading of the following preceding paper, also at the Phys. Rev., is instructive
Can the generalized Haag theorem be further generalized?
It should be noted that the results reported above solely present
the version published by Phys. Rev. and not the complete research
conducted by Santilli. In essence, the editors of Phys. Rev. kept
the paper for years without accepting it and without rejecting it,
evidently due to the absence of a credible technical
counter-arguments (in the 1970s, technical arguments were required
for a rejection, something abandoned these days at the
American and other Physical Societies).
Santilli finally understood the reason for the delay, changed the
final parts, and the paper was accepted and published immediately
thereafter. The political problems were multifold. The first problem was caused by
the conclusion stating that, {\it in the event a given discrete symmetry and
its dual are violated, the Wightman axioms are violated too.} This
evident conclusion had to be removed from the paper for its
publication, as confirmed by Santilli recollections, because
Wightman was in control of quantum field theory of the time.
The biggest political problem, was, however, caused by Santilli's
analytic continuation of a discrete symmetry to its connected
component as expected from Lie's theory, namely, {\it the
achievement of the original goal of deriving the lack of exact
character of the (continuous) Lorentz transformations from the
violation of a discrete symmetry.} Unfortunately, the Foundation
could not identify any of Santilli's original manuscripts in the
ield. Following consultation, Santilli released the following
statement:
%
A direct test of the applicability or inapplicability of
special relativity under conditions violating discrete symmetries
was inconceivable in the 1970s as it is inconceivable today due to
organized opposing interests controlling major particle laboratories
around the world.
This scientific obscurantism is implemented despite the
evidence that a theory, such as special relativity, that is strictly
invariant under time reversal, cannot possibly be exact for a
strictly irreversible process, such as a weak interaction decay,
since the scattering amplitude is invariant under time reversal,
thus predicting the spontaneous recombination of the debris of the
decay into the original particle.
Due to this unfortunate political control of basic physical
knowledge, in the 1970s I asked myself whether there was any way of
establishing the lack of exact character of the connected component
of the Lorentz symmetry from the violation of its discrete
component. To my best recollection, I did find an analytic
continuation connecting said components in such a way that the
violation of one would imply that of the other.
However, for scientific honesty, I have to stress that I am not
sure whether the derivation was correct due to lack of its technical
review by the American Physical Society. Also, in view of the
extreme complexity of the field in which I have not conducted
research for some thirty years, I do not have the time to reconsider
it now.
I am proud for my reputation of never accepting abuses without
due response. In this particular case, the defense of the Ph. D.
thesis of my student Ktorides was at stake because crucially
dependent on the publication of the paper by Phys. Rev. Hence, I had
to accept the political manipulation of the conclusions by the editors of Phys. Rev.
and their referees to allow Ktorides graduation.
Following the appearance of the 1974 paper, I destroyed the
entire file out of sheer rage that, in a seemingly democratic
country, the American Physical Society was allowed such a
totalitarian control of fundamental human knowledge in complete
impunity and without any control by the country.
The Foundation is interested in supporting research on
``Santilli problem in quantum field theory," namely, whether there
is an analytic continuation or other mechanism under which the
violation of a discrete symmetry causes the inapplicability of the
Lorentz symmetry and special relativity.
3.7. RESOLUTION OF THE HISTORICAL IMBALANCE ON ANTIMATTER (1994)
3.7A. Foreword
Santilli has conducted comprehensive studies on antimatter at all possible levels, from Newtonian mechanics to second quantization and for conditions of increasing complexity, from fully conservative conditions to the most general possible irreversible non-Hamiltonian conditions, as well as hyperstructural conditions expected in possible antimatter living structures.
In this section we outline the most elementary level of study, that for point-like abstractions of antiparticles under sole potential interactions. The subsequent levels of study are given by the broader isodual isotopic, genotopic and hyperstructural theories that cannot possibly be reviewed in this presentation, but can be constructed via an isodual map of matter theories.
3.7B. Newton-Santilli isodual equation for antimatter
As recalled in Section 1.4, no consistent classical theory of antimatter existed prior to Santilli's research, to our best knowledge. For instance, by resuming the use of the conventional associative multiplication axb = ab, the celebrated Newton's equation
Thanks to the prior discovery of his isodual mathematics outlined in Chapter 2, Santilli developed the isodual theory of antimatter that holds at all levels of study, thus restoring full democracy between matter and antimatter.
In essence, in the 20th century antimatter was empirical treated by merely changing the sign of the change, under the tacit assumption that antimatter exists in the same space as that for matter. Thus, both matter and antimatter were studied with respect to the same numbers, fields, spaces, etc. However, a correct classical representation of antimatter required a mathematics that is anti-isomorphic to that used for matter as a necessary condition to admit a charge conjugated operator image.
Santilli represents antimatter via his anti-Hermitean isodual map (2.9) that must be applied to the totality of quantities used for matter and all their operations. Hence, under isoduality, we have not only the change of the sign of the charge, but also the isodual conjugation of all remaining physical quantities (such as coordinates, momenta, energy, spin, etc.) and all their operations. This is the crucial feature that allows Santilli to achieve a consistent representation of antimatter also for neutral bodies.
We have in this way the Newton-Santilli isodual equation for antiparticles that we write in the simplified form
Note that, after working out all isodual maps, antiparticle equation (3.19) merely yields minus the value of the conventional equation for particles in both the l.h.s. and the r.h.s, thus appearing to be trivial. However, a most important feature of the above equation is that it defines antiparticles in a new space, the Euclid-Santilli isodual space, that is coexistent but different than our own space. The Euclidean space and its isodual then form a two-valued hyperspace.
In this section we shall show that, starting from the fundamental equation (3.19), the isodual theory of antimatter is consistent at all subsequent levels, including quantization, at which level it is equivalent to charge conjugation.
Note that isodual antiparticles have a negative energy. This feature is dismissed by superficial inspections as being nonphysical, thus venturing judgments prior to the acquisition of technical knowledge. In fact, negative energies are indeed nonphysical, but when referred to our spacetime, that is, with respect to positive units of time. By contrast, when referred to negative units, all known objections on negative energies become inapplicable, let alone resolved.
Note also that isodual antiparticles move backward in time. This view was originally suggested by Stueckelberger in the early 1900s, and then adopted by various physicists, such as Feynman, but dismissed because of causality problems when treated with our own positive unit of time. Santilli has shown that motion backward in time referred to a negative unit of time td = - t is as causal as motion forward in time referred to a positive unit of time t, and this illustrates the nontriviality of the isodual map.
where Wμ ν is the energy-momentum tensor due to weak and strong interactions in the interior of the πo and w is another constant.
>From the evident differences between Eqs. (3.4) or (3.5) and (3.6), Santilli concluded that: Einstein conception of gravitation as pure curvature is irreconcilably incompatible with quantum electrodynamics because, either
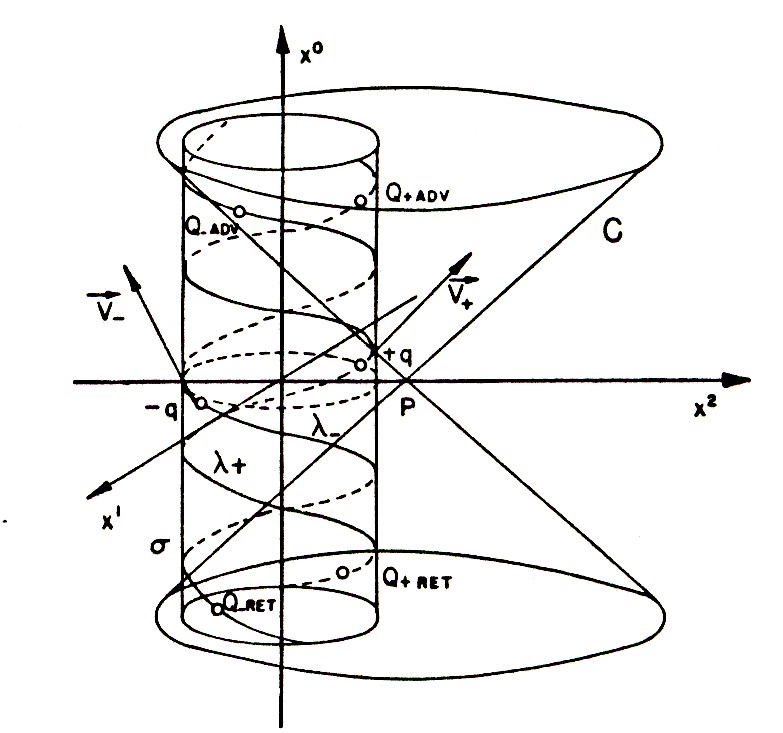
Figure 3.4. A schematic view of the calculations via advanced and retarded field theoretical methods, used by Santilli in 1974 to establish the incompatibility of Einstein's gravitation with quantum electrodynamics, in this case showing the entire electromagnetic origin of the exterior gravitational mass of the πo particle, in irreconcilable disagreement with the null source of Einstein's field equations for the case considered.
R. M. Santilli,
(MIT) Annals of Physics Vol. 13, 108-157 (1974)
Ruggero Maria Santilli
Galilean Electrodynamics, Summer 2006, p. 43-79 (2006)
R. M. Santilli, International Academic Press (2008)
where: SO6(3.1) represents the connected 6-dimensional Lorentz symmetry; T4(3.1) is the group of translations in Minkowski spacetime; and ⊗ is the semidirect product.
with group structure
and generators of the Lie algebra
where: Jμν and Pμ are the conventional generators of the Poincare' algebra; Xμ is a position operator, and E is the energy operator, the latter operators being a novelty of the new symmetry since they are impossible for the Poincare' symmetry. For additional technical data, interested readers are suggested to consult the literature below.
A. Aghassi, P. Roman and R. M. Santilli,
Phys. Rev. D vol. 1, 2753-2765 (1970)
A. A. Aghassi, P. Roman and R. M. Santilli,
Nuovo Cimento Vol. 5, pages 551-590 (1971)
H. E. Wilhelm,
Hadronic J. Vol. 31 (2008) in press
J. R. Fanchi,
Hadronic J. Vol. 31 (2008) in press
The PCT theorem within the context of vacuum expectation values (VEV) verifying Wightman's axioms essentially related the PCT conditions to the weak local commutativity conditions (WLC) under the assumption of Lorentz invariance for the vacuum expectation values plus, boundedness of the energy from below and other conditions permitting smooth analytic continuations.
and proved the following:
The implications of the above discovery presented in the papers quoted below are the following: For quantum field theories admitting discrete symmetries, Santilli's Theorem 3.6A implies the validity of basically new discrete symmetry that can be experimentally verified. For theories violating any discrete symmetry, Theorem 3.6A. implies that, whenever a discrete symmetry is violated, the corresponding dual symmetry has to be violated too, and vice versa.
The original 1974 paper can be downloaded from the following link
R. M. Santilli and C. N. Ktorides,
Phys. Rev. D Vol. 10, 3396-3406 (1974)
R. M. Santilli and C. N. Ktorides,
Phys. Rev. D Vol. 7, 2447-2456 (1973)
or the celebrated Newton's gravitation
solely apply for matter, and have no means whatsoever to distinguish between matter and antimatter for the very simple reason that antimatter was inconceivable at Newton's times.
where "d" denotes isodual map (2.9), and the same conjugation holds for gravitation (see below).
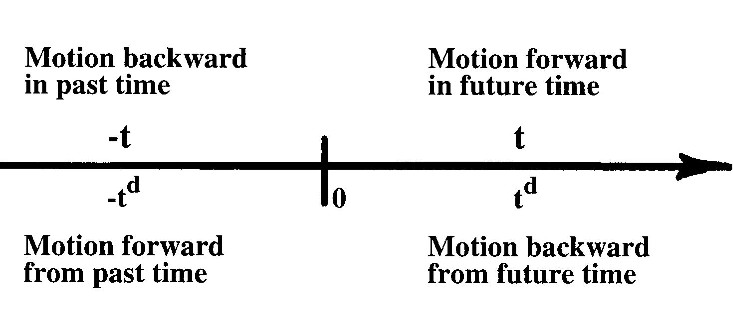
Figure 3.5. Contrary to popular beliefs, time has four directions as depicted by Santilli in this figure to illustrate the need for isoduality. In fact, time reversal can only allow the representation of two time directions. The remaining two time directions can solely be represented via the isodual map.
Moreover, the assumption that particles and antiparticles have opposing directions of time is the only one known giving hopes for the understanding of the process of annihilation of particles and their antiparticles, a mechanisms utterly incomprehensible for the 20th century physics.
3.7C. Isodual representation of the Coulomb force
The isodual theory of antimatter verifies all classical experimental evidence on antimatter because it recovers the Coulomb law in a quite elementary way. Consider the case of two particles with the same negative charge and Coulomb law
where the positive value of the r.h.s is assumed as representing repulsion, and the constant is assumed to have the value 1 for simplicity.
Under isoduality, the above expression becomes
thus reversing the sign of the equation for matter, Fd = - F. However, antimatter is referred to a negative unit of the force, charge, coordinates, etc (Chapter 2). Hence, a positive value of the Coulomb force referred to a positive unit representing repulsion is equivalent to a negative value of the Coulomb force referred to a negative unit, and the latter also represents repulsion.
For the case of the electrostatic force between one particle and an antiparticle, the Coulomb law must be projected either in the space of matter
representing attraction, or in that of antimatter
in which case, again, we have attraction, thus representing classical experimental data on antimatter.
3.7D. Hamilton-Santilli isodual mechanics
To proceed in his reconstruction of full democracy in the treatment of matter and antimatter, Santilli had to construct the isodual image of Hamiltonian mechanics because essential for all subsequent steps. In this way he reached what is today called the Hamilton-Santilli isodual mechanics based on the isodual equations
and their derivation from the isodual action Ad (a feature crucial for quantization), from which the rest of the Hamilton-Santilli isodual mechanics follows.
3.7E. Isodual special and general relativities
As indicated in Section 1.4, special and general relativities are basically unable to provide a consistent classical treatment of antimatter. Santilli has resolved this insufficiency by providing a detailed, step by step isodual lifting of both relativities with a mathematically consistent representation of antimatter in agreement with classical experimental data (see below for the quantum counterpart).
The reader should be aware that the above liftings required the prior isodual images of the Minkowskian geometry, the Poincare' symmetry and the Riemannian geometry, as well as the confirmation of the results with experimental evidence.
3.7F. Prediction of antigravity
Studies on antigravity were dismissed and disqualified in the 20-h century on grounds that "antigravity is not admitted by Einstein's general relativity." This posture resulted in a serious obscurantism because general relativity cannot represent antimatter, thus being disqualified for any serious statement pertaining to the gravity between matter and antimatter.
Thanks to his isodual images of special and general relativity, Santilli has restored a serious scientific process in the field, by admitting quantitative studies for all possibilities, and has shown that once antimatter is properly represented, matter and antimatter must experience antigravity (defined as gravitational repulsion) because of supporting compatible arguments at all levels of study, with no known exclusion. In fact, all known "objections" against gravitational repulsion between matter and antimatter become inapplicable under Santilli isoduality, let alone meaningless.
The arguments in favor of the above conclusion are truly forceful because differentiated and mutually compatible. As a trivial illustration, we have the repulsive Newton-Santilli force between a particle and an isodual particle (antiparticle) both treated in our space
which is indeed repulsive. The same conclusion is reached at all levels of study.
It should be indicated that a very compelling aspect supporting antigravity between matter and antimatter is Santilli's identification of gravity and electromagnetism indicated in Section 3.4. In fact, the electromagnetic origin of exterior gravitation mandates that gravity and electromagnetism must have similar phenomenologies, thus including both attraction and repulsion.
3.7G. Test of antigravity
Santilli has proposed an experiment for the final resolution as to whether antiparticles in the gravitational field of Earth experience attraction or repulsion. The experiment consists in the measure of the gravitational force of a beam of positrons in flight on a horizontal vacuum tube 10 m long at the end of which there is a scintillator. Then, the displacement due to gravity is visible to the naked eye under a sufficiently low energy (in the range of the 10-3 eV). The experiment was studied by the experimentalist Mills and shown to be feasible with current technologies and resolutory.
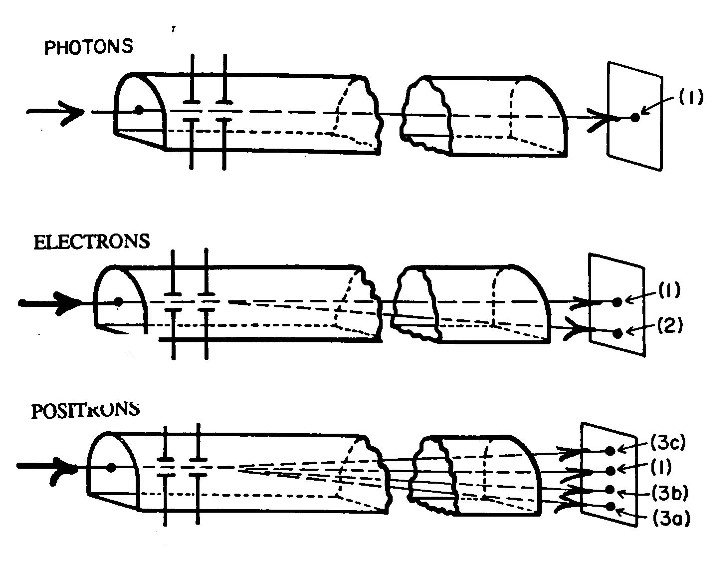
Figure 3.6. The original illustration used by Santilli for the 1994 proposal to test the gravity of positrons in horizontal flight in a vacuum tube. The proposal has been qualified by experimentalists as being technically feasible nowadays and resolutory because the displacement due to gravity on a scintillator at the end of a 10 m flight for positrons with milli-eV energy is visible to the naked eye. The usual criticisms based on disturbances caused by stray fields have been disqualified as political for a tube with at least 50 cm diameter. Virtually all major physics laboratories around the world have rejected even the consideration of the test, despite its dramatically lower cost and superior scientific relevance compared to preferred tests, on grounds that "Einstein theories do not admit antigravity," although with documented knowledge that said theories cannot consistently represent antimatter as reviewed in the test.
3.7H. Isodual quantum mechanics
Next, Santilli constructed a step-by-step image of quantum mechanics under his isodual map based on the Heisenberg-Santilli isodual time evolution for an observable Q
and related isodual canonical commutation rules, Schroedinger-Santilli isodual equations, etc.
He then proved that, at the operator level, isoduality is equivalent to charge conjugation.
Consequently, the isodual theory of antimatter verifies all experimental data at the operator level too. Nevertheless, there are substantial differences in treatment, such as:
1) Quantum mechanics represents antiparticles in the same space of particles, while under isoduality particles and antiparticles exist in different yet coexisting spaces;
2) Quantum mechanics represents antiparticles with positive energy referred to a positive unit, while isodual antiparticles have negative energies referred to a negative unit;
3) Quantum mechanics represents antiparticles as moving forward in time with respect to our positive time unit, while isodual antiparticles move backward in time referred to a negative unit of time.
3.7I. Experimental detection of antimatter galaxies
Recall from Chapter 2 that the isodual theory of antimatter was born out of Santilli's frustration as a physicist for not being able to ascertain whether a far away star, galaxy or quasar is made up of matter or of antimatter. Santilli has resolved this uneasiness via his isodual photon γd namely, photons emitted by antimatter that have a number of distinct, experimentally verifiable differences with respect to photons γ emitted by matter,
thus allowing, in due time, experimental studies on the nature of far away astrophysical objects.
A most important difference between photons and their isoduals is that the latter have negative energy, as a result of which, isodual photons emitted by antimatter are predicted to be repelled in the gravitational field of matter. A possibility for the future ascertaining of the character of a far away star or quasar is, therefore, the test via neutron interferometry or other sensitive equipment, whether light from a far away galaxy is attracted or repelled by the gravitational field of Earth (for other possibilities see the literature quoted below).
3.7J. The new isoselfdual invariance of Dirac's equation
Santilli has released the following statement on the Dirac equation:
I never accepted the interpretation of the celebrated Dirac equation as presented in the 20-th century literature, namely, as representing an electron, because the (four-dimensional) Dirac's gamma matrices are generally believed to characterize the spin 1/2 of the electron. But Lie's theory does not allow the SU(2)-spin symmetry to admit an irreducible 4-dimensional representation for spin 1/2, and equally prohibits a reducible representation close to the Dirac's gamma matrices.
Consequently, Dirac equation cannot represent an electron intended as an elementary particle since elementarily requires the irreducible character of the representation. In the event Dirac's gamma matrices characterize a reducible representation of the SU(2)-spin, Dirac's equation must represent a composite system.
I discovered the isodual theory of antimatter by examining with care Dirac's equation. In this way, I noted that its gamma matrices contain a conventional two-dimensional unit I2x2 = Diag. (1, 1), as well as a conjugate negative-definite unit - I2x2. That suggested me to construct a mathematics based on a negative definite unit. The isodual map come from the connection between the conventional Pauli matrices σk, k = 1, 2, 3, referred to I2x2 and those referred to - I2x2. In this way I reached the following interpretation of Dirac's gamma matrices as being the tensorial product of I2x2, σk times their isoduals,
Therefore, I reached the conclusion that the conventional Dirac equation represents the tensorial product of an electron and its isodual, the positron. In particular, there was no need to use the "hole theory" or second quantization to represent antiparticles since the above re-interpretation allows full democracy between particles and antiparticles, thus including the treatment of antiparticles at the classical level, let alone in first quantization.
By continuing to study Dirac's equation without any preconceived notion learned from books, I discovered yet another symmetry I called isoselfduality, occurring when a quantity coincides with its isodual, as it is the case for the imaginary unit id = i. In fact, Dirac's gamma matrices are isoselfdual,
This new invariance can have vast implications, all the way to cosmology, because the universe itself could be isoselfdual as Dirac's equation, in the event composed of an equal amount of matter and antimatter. In conclusion, Dirac's equation is indeed one of the most important discoveries of the 20-th century with such a depth that it could eventually represent features at the particle level that actually hold for the universe as a whole.
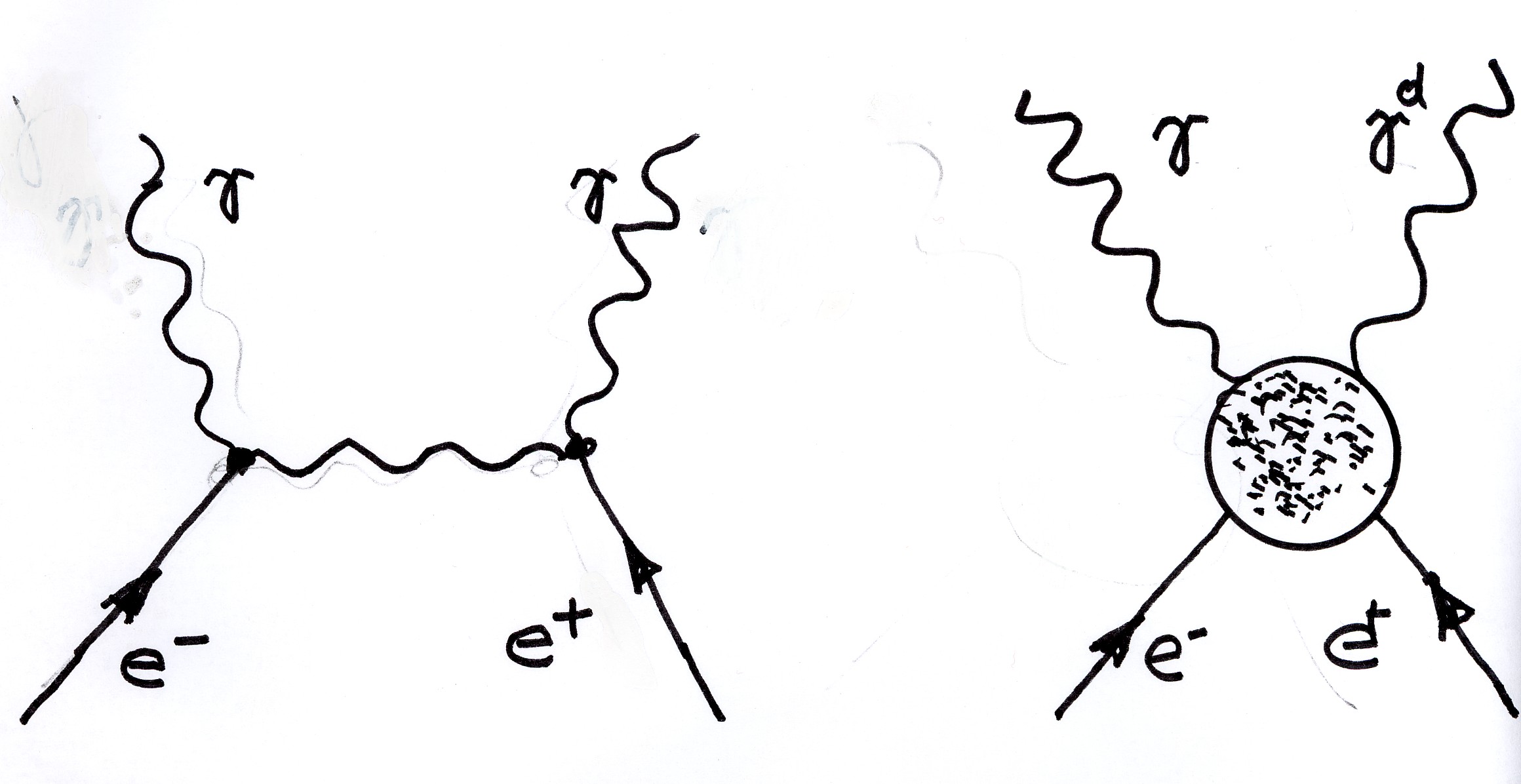
Figure 3.7. An illustration of the serious implications of Santilli's isodual theory of antimatter: the need for a revision of the scattering theory of the 20th century due to its violation of the isoselfdual symmetry of Dirac's equation. The diagram in the left illustrates the isoselfduality of the initial particles (an electron and a positron) but its violation in the final particles (two identical photons). The diagram in the right illustrates one of the several needed revisions, the use for final particles of a photon and its isodual as a necessary condition to verify the new isoselfdual symmetry. Additional dramatic revisions are due to the purely action-at-a-distance, potential interactions of the conventional scattering theory (represented with a waving central line in the left diagram), compared to the non-Hamiltonian character of the scattering region caused by deep penetrations of the wavepackets of particles (represented with a circle in the right diagram). A review of the novel hadronic scattering theory is presented in Chapter 5.
3.7K. Dunning-Davies thermodynamics for antimatter
As well known, the sole formulation of thermodynamics of the 20-th century was for matter. The first consistent formulation of thermodynamics for antimatter has been reached by J. Dunning-Davies with intriguing implications for astrophysics and cosmology yet to be explored, see the original contribution by Dunning Davies quoted below
3.7L. Isoselfdual spacetime machine
A "spacetime machine" is generally referred to a mathematical process dealing with a closed loop in the forward spacetime cone, thus requiring motions forward as well as backward in time. As such, the "machine" is not permitted by causality under conventional mathematical treatment, as well known.
Santilli discovered that isoselfdual matter, namely, matter composed by particles and their antiparticles such as the positronium, have a null intrinsic time, thus acquiring the time of their environment, namely, evolution forward in time when in a matter field, and motion backward in time when in an antimatter field.
Consequently, Santilli showed that isoselfdual systems can indeed perform a closed loop in the forward light cone without any violation of causality laws, because they can move forward when exposed to a matter and then move backward to the original starting point when exposed to an antimatter.
3.7M. Original literature
Santilli's original papers on the discovery of isomathematics have been identified in Chapter 2. To our best knowledge, Santilli's first paper on the isodual theory of antimatter is the following one dating to 1994 (following the 1993 paper on isodual numbers)
Representation of antiparticles via isodual numbers, spaces and geometries
R. M. Santilli,
Comm. Theor. Phys. Vol. 3, 153-181 (1994)
The first presentations of the classical isodual theory, antigravity, the isodual photon and the isoselfdual spacetime machine appeared in the following papers
Classical isodual theory of antimatter and its
prediction of antigravity
R. M. Santilli,
Intern. J. Modern Phys. A Vol. 14, 2205-2238 (1999)
Antigravity
R. M. Santilli,
Hadronic J. Vol. 17, 257-284 (1994)
Does antimatter emit a new light?
R. M. Santilli,
Hyperfine interactions Vol. 109, 63-81 (1997)
Spacetime machine
R. M. Santilli,
Hadronic J. Vol. 17, 285-310 (1994)
An independent study by an experimentalist on the feasibility and resolutory character of the proposed measurements of the gravity of positron in horizontal flight on Earth can be found in the following paper
Comprehensive presentation of the isodual theory of antimatter are available in the monographs
"Elements of Hadronic Mechanics"
Vol. II: "Theoretical Foundations"
"Isodual Theory of Antimatter, with Applications to Antigravity, Grand Unification and Cosmology,"
The first formulation of thermodynamics for antimatter was reached by J. Dunning Davies in the paper
Isodual thermodynamics for antimatter
3.8. INITIATION OF q-DEFORMATIONS OF LIE THEORY (1967)
As part of his Ph. D. Thesis at the University of Torino, Italy, Santilli proposed in 1967
Embedding of Lie-algebras in nonassociative structures
the first mutations (today known as "deformations") of Lie algebras known in the mathematical and physical literature of the time with the product (where we return to use the convcentional notation of the associative product ab)
The proposal was made as a first approximation of Lagrange and Hamilton's legacy (Section 2.1), namely, via a generalization of the analytic equations approximating external terms for open, nonconservative and irreversible systems while reconstructing an algebra in the brackets of the time evolution.
In fact, in his 1967 paper and others of that period (see the Curriculum) Santilli writes the deformed analytic equations in the form
In this way, Santilli realized Jordan's dream of seeing his algebras appear in physics applications, although at the level of a covering of quantum mechanics, since the latter has no possible content of Jordan algebras. Santilli also worked out the classical image of the above formulation in which the Lie-admissible character persists, although the Jordan-admissible character is lost.
Santilli's presented his mutations (deformations) of Lie algebra in his paper of 1967 via the most general possible formulation, that in which the product AB is nonassociative, with the clear identification of its associative particular form, Subsequent vast studies in mutations were conducted as part of hadronic mechanics and, as such, they are discussed below.
As it is well known, in 1989 L. Biebernarn and R. Macfairlane published their
papers on the simpler $q$-deformations with product $(A, B) = AB -
qBA$ without any quotation of Santilli's origination of 1967 [30], even
though they were fully aware of it (Biedenharn joined Santilli in
the early 1980s for a DOE grant application precisely on Santilli's
mutations/deformations, and Macfairlane was directly
informed by Santilli years prior to 1986).
%
In particular, Biedenharn and Macfairlane changed Santillis
original, algebraically more appropriate term of ``mutations" into
``deformations," and avoided the identification of their
Lie-admissible and Jordan admissible character to prevent an
instantaneous identification of Santilli's origination, due to his
known expertise in these algebras.
Following these publications, thousands of papers on
$q$-deformations appeared in the physics literature generally
without any quotation of Santilli's origination. As a result of these occurrences, Santilli has been dubbed the most plagiarized physicist of the 20-th century.
3.9. THEOREMS OF CATASTROPHIC INCONSISTENCIES OF
3.9A. The majestic consistency of Hamiltonian theories.
Santilli has always considered classical Hamiltonian mechanics and its operator image, quantum mechanics (hereoihereon referred to as "Hamiltonian theories"), as having a majestic consistency, due not only to their mathematical rigor permitted by their underlying Lie's theory and its body of methods, but also to the physical consistency of their axiomatic structure.
Consider the fundamental dynamical equations of quantum mechanics, Heisenberg's equations for the characterization of the time evolution of an observable Q(t) in the finite and infinitesimal forms
The implications of the above simple property are far reaching. To begin, the time evolution of quantum mechanics leaves invariant the basic unit, generally assumed to be that of the Euclidean space, I = Diag. (1, 1, 1),
3.9B. Theorems of catastrophic inconsistencies of noncanonical and nonunitary theories.
The limitations of Hamiltonian theories in face of the complexity of nature was seen in the last decades of the 20th century by several physicists, resulting in the proposal of a considerable number of generalized theories, much along the development of hadronic mechanics.
However, unlike hadronic mechanics, researchers generalized Hamiltonian formulations on one side, while preserving conventional mathematics, on the other side. A major scientific contribution by Santilli's group has been that of identifying the inconsistencies of generalized theories conceived along these lines, that can be expressed via the following:
THEOREM 3.9A: All theories with a nonunitary time evolution ,
Mathematical inconsistencies: Let I be the unit of the base field at a given time t. But the time evolution cannot preserve such a unit by definition,
Physical inconsistencies: Nonunitary theories do not preserve over time the basic units of measurements, because, from the very definition of a nonunitary transform, we have
Also, nonunitary theories do not admit the same numerical predictions under the same conditions at different times, because, for instance, one can select a nonunitary transform for which
The case for classical noncanonical theories formulated with the mathematics of canonical theories have corresponding, catastrophic, mathematical and physical inconsistencies.
3.9C. Examples of catastrophically inconsistent theories.
Numerous theories afflicted by the inconsistencies here considered have been and continue to be developed. Examples of classical catastrophically inconsistent, noncanonical theories are given by:
1) Newton's equations with nonselfadjoint (nonpotential) forces;
2) Lagrange and Hamilton analytic equations with external terms;
3) Lagrange and Hamilton's equations without external terms but with Lagrangians and Hamiltonians of second or higher order (depending on accelerations or its time derivatives);
4) Birkhoffian mechanics (even though preserving a Lie structure) because noncanonical;
5) Hamilton-admissible mechanics;
Examples of operator, catastrophically inconsistent nonunitary theories are:
A) (p, q)-, q-, k- or any other deformations of Lie algebras;
B) The so-called "deformed quantum mechanics";
C) The so-called "deformed Lorentz symmetry";
D) The so-called "deformed special relativity";
E) Theories with a complex-valued Hamiltonian to represent dissipativity, e.g., in nuclear physics;
F) The so-called quantum groups;
G) The so-called "squeezed states";
H) String theories when including gravitation on a curved space;
I) Quantum gravity;
J) Nonunitary statistics, such as that by Prigogine;
K) Supersymmetric models;
L) The Kac-Moody algebras;
and others.
The literature also contains a number of additional theories suffering of catastrophic inconsistencies not necessarily connected to nonunitarity, among which we mention theories nonlinear in the wavefunction ψ, namely with eigenvalue equations in Hermitean Hamiltonians of the type
Other catastrophically inconsistent theories are those with a nonassociative enveloping algebra, such as Weinberg's nonlinear theory with a time evolution of the type
3.9D. Original literature
Inconsistencies of theories with a nonassociative enveloping algebras were studied in the following paper after an initial suggestion by S. Okubo dating back to 1982 (of which the Foundation failed to identify the related paper until now). The studies were then resumed by A. Jannussis, R. Mignani and R. M. Santilli in 1993 with the paper
Problematic aspects of Weinberg's nonlinear theory
additional studies can be located in the paper
Algebraic inconsistencies of a class of equations for the description of open systems and their resolution via Lie-admissible algebras
Problematic aspects of q-deformations and their isotopic resolution
Origin and axiomatization of q-deformations
Santilli then conducted comprehensive studies on the Inconsistency Theorems in the following papers
Origin, problematic aspects and invariant formulation of q-, k- and
other quantum deformations
Origin, problematic aspects and invariant formulation of classical and operator deformations
Nine theorems of catastrophic inconsistencies of general relativity and their possible resolution via isogravitation
New problematic aspects of current string theories and
their invariant resolution
Lie-admissible invariant representation of irreversibility for matter and antimatter at the classical and operator level
3.10. SANTILLI RELATIVITIES (1978)
3.10A. Historical notes
As indicated by W. Pauli in one of the footnotes of his famous book Theory of Relativity, H. A. Lorentz attempted in 1895 the construction via Lie's theory of the symmetry leaving invariant the locally varying speed of light within physical media, C = c/n, where c is the speed of light in vacuum and n the familiar index of refraction. However, he encountered unsurmontable difficulties, and had to restrict the study to the constancy of the speed of light in vacuum c, resulting in the now historical paper of 1904 presenting the celebrates Lorentz symmetry with connected component SO(3.1).
Santilli studied Pauli's book very carefully, identified the footnote presenting the unsolved problem, and called it the Lorentz problem, again, referring to the construction of the symmetry leaving invariant the locally varying speed of light C = c/n, such as for light traveling through liquids, atmospheres, chromospheres, etc., and initiated the research for its solution that resulted to be of such a complexity to require a lifetime of study.
By looking in retrospect, Santilli's most important contributions for Lorentz's problem have been:
1) The proof that the problem cannot be solved with Lie's theory because, even assuming that a solution is found empirically, that solution is catastrophically inconsistent in view of the Theorems of Section 3.9;
2) The construction of the iso-, geno- and hyper coverings of Lie's theory and their isoduals permitting indeed the construction of an invariant solution for physical media of matter and antimatter, respectively; and
3) Constructing step by step iso-, geno- and hyper- and isodual generalizations of all main aspects pertaining to the Lorentz symmetry, from numbers to special relativity, and proving that said covering theories verify available experimental evidence for the intended conditions of applicability.
Evidently, we cannot possibly review here this lifetime of work. Hence, we shall restrict our presentation to the sole case of Santilli isorelativity with original contributions in free pdf downloads, and merely indicate the references of the remaining relativities.
3.10B. Santilli's opening statement
For one of the seminars delivered at physics departments around the world, Santilli brought in the lecture room a small rubber ball, a glass filled up with water, a picture of far away galaxies, pictures of Sun light at the Zenith, Sunset and Sunrise, and a cigarette lighter. He then initiated the seminar with the following opening words:
Einstein's special relativity has a majestic axiomatic structure and a truly impressive body of experimental verifications for the conditions of its original conception, point-like particles and electromagnetic waves propagating in vacuum conceived as empty space. In view of these historical successes, it has been widely believed in the 20th century that special relativity is valid for whatever conditions exist in the universe. In reality, there exist numerous conditions, beyond those of the original conception, under which special relativity is only "approximately valid" or "inapplicable" and cannot be claimed to be violated in respect to Albert Einstein, because the theory was not conceived for these broader conditions. Among a variety of these conditions, I bring to your attention the following five cases of visual evidence on the inapplicability of special relativity:
1) The squeezing of this rubber ball cannot be treated by special relativity or quantum mechanics due to their incompatibility with the deformation theory that would causes the breakdown of the central pillar of both theories, the rotational symmetry. This limitation carries on all the way to hadron physics since protons and neutrons are extended and, therefore, have to be deformable with numerous important implications, for instance, for a quantitative representation of nuclear magnetic moments;
2) The simple phenomenon of the refraction of light causing the apparent bending of a stick in this glass of water also cannot be represented with special relativity because the occurrence can be solely represented quantitatively via a decrease of the speed of light in water, thus terminating the belief on the "universal" constance of the speed of light, since its reduction to photons scattering among liquid molecules has been disqualified for lack of quantitative representation of all electromagnetic waves propagating in water, such as for radiowaves with 1 m wavelength for which the reduction to photons has no physical sense;
3) When looking at this picture of far away galaxies, special relativity cannot provide any classical distinction between matter and antimatter galaxies since the sole distinction admitted by special relativity is that of the sign of the charge while far away galaxies must be assumed to be neutral. At any rate, antimatter did not exist as yet at the time of Einstein's formulation of special relativity;
4) These pictures of Sun light at the Zenith, Sunset and Sunrise constitute evidence visible to the naked eye of the inapplicability of special relativity within physical media such as our atmosphere because the first picture established the transparency of our atmosphere to blue light, thus preventing its absorption at the horizon, while the remaining two pictures establish the existence of a redshift that cannot possibly follow relativity laws because, assuming it exists at Sunset, it cannot exist at Sunrise since Earth moves away from the Sun at Sunset while it moves toward the Sun at Sunrise. Hence, according to special relativity, we should have a distinct redshift at Sunset and an equally distinct blueshift at Sunrise. The dominance of the red at both Sunset and Sunrise, therefore, establishes the existence of a basically new behavior of light propagating within physical media beyond that of light propagating in vacuum;
5) Special relativity and quantum mechanics are inapplicable to energy releasing process, such as the flame in this cigaret lighter, because all energy releasing processes are irreversible over time, while special relativity and quantum mechanics are strictly reversible and consequently predict that the flame and the smoke should recombine themselves spontaneously into the original fuel. In any case, special relativity and quantum mechanics had to be built with reversible axioms as a necessary condition to represent the physical problems in the early part of the 20th century, such as electrons orbiting in an atomic structure. Consequently, special relativity and quantum mechanics cannot credibly be assumed as being valid for the dramatically different irreversible processes.
In this seminar I shall indicate that, thanks to the use of new mathematics specifically constructed for the problems at hand, it is possible to construct sequential coverings of special relativity and quantum mechanics providing a more adequate treatment of the above five physical conditions.
I would like to stress ab initio that I do preserve Einstein's axioms and merely present broader realizations. In different words, my way of honoring the memory of Albert Einstein is not that of adapting nature to his original formulations with consequential risk of condemnations by posterity, but instead I honor Einstein by providing a dramatic broadening of the conditions of applicability of his axioms.
In this section we provide an outline of the latter objectives as well as free pdf downloads of Santilli's original contributions at times of difficult identification in the libraries.
3.10C. Conceptual foundations
Santilli always considered the widespread claim of the "universal constancy of the speed of light" a political posture because, as indicated in Section 1.2, the scientific statement should be "constancy of the speed of light in vacuum," since that is the sole case with experimental verifications.
Therefore, Santilli never accepted special relativity for the characterization of dynamics within physical media because most media are opaque to light. Hence, the assumption of the speed of light in vacuum as the maximal causal speed within physical media opaque to light was repugnant to him. He then searched for a geometric characterization that would replace the speed of light within physical media, in such a way to recover, of course, the speed of light when propagation returns to be in vacuum.
Santilli was also unable to accept special relativity for media that are transparent to light, such as liquids, atmospheres, chromospheres, etc., for various reasons, Consider, for instance, the propagation of light in water. In this case electrons can propagate faster than the local speed of light, producing the known Cerenkov light. He argued that, if the speed of light in vacuum is assumed as the maximal causal speed in water to salvage causality, there is the violation of a fundamental relativistic principle because the sums of two light speeds in water does not yield the speed of light in water. Alternatively, if one assumes the speed of light in water as the maximal causal speed, the relativistic addition of speeds is salvaged but special relativity would violate causality.
The usual posture of attempting to salvage special relativity via the reduction of light to photons scattering through atoms was dismissed as political, because such a reduction has no physical value for electromagnetic waves with large wavelength, such as of 1 meter wavelength, which electromagnetic waves also propagate in water at a reduced speed according to the law C = c/n.
By keeping these aspects in mind and their experimental verifications established in Chapter 5, the biggest physical implications of Santilli's studies is that matter causes a mutation of the very structure of conventional Minkowskian spacetime. In any case, deviations from Einsteinian predictions within matter could not exist without such a mutation.
Along the latter lines, by far the biggest deviations from special relativity are expected by Santilli within physical media that are inhomogeneous (due to a local change of density) and anisotropic (due to differences in different space directions) such as atmospheres, chromospheres, etc., because these media have geometric deviations from the homogeneity and isotropy of the Minkowski spacetime.
In studying the original contributions, interested scholars are, therefore, suggested to pay particular attention to the interplay between geometry, algebras and physics.
3.10D. Mathematical foundations
The problem solved by Lorentz was the invariance of the Minkowskian metric m = Diag. (1, 1, 1, - c2). The problem solved by Santilli was the invariance of the broader metric m* = Diag. (1, 1, 1, - c2/n2), where n is a rather complex function of all needed local variables. It is evident that the latter metric can be solely connected to the former via a noncanonical transformation at the classical level or a nonunitary transform at the operator level. Assuming this main characteristic also assures the exiting from the class of equivalence of the Lorentz symmetry.
Hence, Santilli considered the noncanonical transform of m into the most general possible diagonal metric m* with signature (+, +, +, -)
The n's are called the characteristic quantities of the medium considered. The inhomogeneity of the medium is represented via a dependence of the n's on the local density μ, the local temperature τ etc., nk(r, μ, τ, ...), k = 1, 2, 3, 4, while the anisotropy is represented by differences between the space and time characteristics quantities. All n's are normalized to the value nk = 1, k = 1, 2, 3, 4, for the vacuum. Additional information on the characteristic quantities have been provided in Section 2.4.
Santilli then looked for the symmetry of the most general possible, symmetric line element in (3+1) dimension with signature (+, +, +, -)
1) Formulated the theory on his iso-Minkowskian space M* (r* , x* , I*) (Section 2.6) with isocoordinates r* = r I*, r = (r1, r2, r3, t), with isoassociative product A x* B = A T B over an isofield F* with isounit I*;
2) Identified the noncanonical transform with the isounit
3) Subjected to the above noncanonical transform the totality of the framework of special relativity, from numbers to physical laws, with no exclusion to avoid catastrophic inconsistencies due to mixing the mathematics of the covering theory with that of the old.
The above assumptions are sufficient to construct the desired symmetry in the most rigorous possible, but also an elementary way. In fact, the indicated use of the noncanonical transforms permits the simple construction of: the isonumbers
3.10E. Invariance and universality of Santilli's isotopies.
It is easy to see that the isotopic formalism of the preceding section is not invariant under both canonical and noncanonical (or unitary and nonunitary) transforms, such as
It is easy to see that, if the above noncanonical or nonunitary transform is reformulated according to Santilli isomathematics, full invariance is reached and Theorem 3.9A is bypassed.
In fact, all noncanonical or nonunitary transforms can be identically reformulated in the isotopic form Z = Z* T1/2,
under which they become isocanonical or isounitary transforms, namely, they reconstruct canonicity or unitarity on isospaces over isofields,
The scholar serious in science should be aware that the regaining of invariance for noncanonical and nonunitary theories has been the very reason for Santilli laborious and momentum discovery and development of his isomathematics.
It is important also to know that Santilli's isotopies of the Minkowskian geometry are "directly universal" in the sense that they admit all infinitely possible mutations of the Minkowski spacetime (universality) directly in the isometric without any need for coordinates transformations (direct universality).
Finally, the reader should keep in mind that Santilli's isospecial relativity (see below) represents dynamical systems with the conventional Hamiltonian (for all potential interactions) and the isounit (for non-Hamiltonian interactions). Consequently, the change of the isounit causes the transition to a different physical system. That is the reason for fixing the isounit in actual applications.
3.10F. Lorentz-Poincare'-Santilli isosymmetry and its isodual
Following, and only following the above laborious preparatory advances, including the achievement of the crucial invariance, it was easy for Santilli to construct the isotopies of the Lorentz and Poincare'
symmetry, today known as Lorentz-Poincare'-Santilli isosymmetry. or at times Poincare'-Santilli isosymmetry.
For clarity and simplicity, in this section we shall outline the projection of the isosymmetry in our spacetime. Thus, we shall avoid using the the symbol "x" to denote conventional multiplication; we shall use the isomultiplication A x* B = A T B when necessary; ordinary symbols J, P, etc., will indicate quantities belonging to the Poincare' symmetry; while symbols with an asterisk will indicate quantities belonging to isospaces over isofields. To begin, the connected component of the Lorentz-Poincare'-Santilli isosymmetry can be written
1) Isorotations (see the references for details),
3) Isotranslations,
In summary, recall that the Poincare' symmetry is ten dimensional. Contrary to all expectations, Santilli's isotopies of the Poincare' symmetry turned out to be eleven dimensional. Hence, Santilli conducted a re-examination of the conventional treatment of special relativity.
The basic unit of the Lorentz and Poincare' symmetries is the 4-dimensional unit matrix I = Diag. (1, 1, 1, 1) > 0, while the unit of the base field universally assumed in special relativity is the trivial unit +1. To avoid this disparity, Santilli assumed the same unit for both the symmetry and the base field, thus using a basic field with unit I. Thanks to his discovery of the isonumber theory, this assumption requires to rewrite scalars from the usual form w, into the isoscalar form w* = w I (see Chapter 2). Consequently, one is forced to rewrite the basic invariant of special relativity in the form
These simple steps allowed the discovery that the Poincare' symmetry is eleven dimensional, rather than ten dimensional as popularly believed in the 20th century, in view of the additional one-dimensional isotopic invariance
Note that m and m* have the same signature (+. +. +. -). Following the above reformulation of the conventional symmetry, we can quote the following
LEMMA 3.10A: The Poincare'-Santilli and the Poincare' symmetries are isomorphic.
The above lemma illustrates Santilli's achievement of broader realizations of the abstract axioms of special relativity. The isodual Poincare'-Santilli isosymmetry for antimatter can be easily constructed via isoduality.
The isotopies of the spinorial covering of the Lorentz-Poincare' symmetry were constructed by Santilli in 1995 and are presented in Section 3.11Q.
Note that the new isotopic symmetry (3.92) remained undiscovered for close to one century. This should not be surprising because its discovery required the prior discovery of new numbers, the isonumbers with an arbitrary unit. Note also from the direct universality of the isotopies, the Poincare'-Santilli isosymmetry provides the invariance for all possible line elements with signature (+, +, +, -), including the Riemannian, Finslerian, Non-Desarguesian and other line elements, by including, as the simplest possible case, the Minkowski line element.
3.10G. Santilli isorelativity and its isodual
Thanks to all the preceding mathematical and physical advances, Santilli has conducted a step-by-step isotopic lifting of the physical laws of special relativity resulting in a new theory today known as Santilli isorelativity. . His central assumption is, again, the preservation under isotopies of the original axioms by Einstein and the introduction of broader realizations. This basic assumption was realized to to such an extent that special relativity and isorelativity coincide at the abstract, realization-free level and, consequently, they could be presented with the same equations only subjected to different realizations of the symbols.
The above conception is evidently permitted by Lemma 3.10A and carries far reaching physical and experimental implications because any criticism on the structure and applications of isorelativity is a criticism on Einstein's axioms, as we shall indicated later on.
Assume for simplicity that motion occurs in the (3, 4)-plane. Then, inhomogeneity of the medium is represented by a functional dependence of n3 on the local density, temperature, etc., n3 = n3(r, μ, τ, ...). Anisotropy of the medium is expressed by the possible difference n3 ≠ n4. Assume that motion is restricted in the (3, 4)-plane, isorelativity can be presented via the following isoaxioms presented in their projection in our spacetime with conventional multiplication:
ISOAXIOM I: The maximal causal speed within physical media is given by
The Doppler-Santilli isoshift admits the following three cases:
1) The isoredshift, namely, a shift toward the red bigger than that predicted by special relativity, generally occurring in anisotropic media of low density, such as planetary atmospheres or astrophysical chromospheres, with values from Eq. (3.98) n4/n3 bigger than 1, and Vmax smaller than c, essentially characterizing the release of energy by light to the medium with consequent decrease of the frequency beyond the value predicted by special relativity;
2) The isoblueshift, namely, a shift toward the blue bigger than that predicted by special relativity, occurring for in anisotropic media of high density, such as astrophysical chromospheres, with values from Eq. (3.98) n4/n3 smaller than 1, and Vmax bigger than c, essentially characterizing the absorption of energy by light from the medium with consequent increase of the frequency beyond the value predicted by special relativity;
3) The conventional Doppler's shift, occurring in transparent isotropic media such as water with n4/n3 = 1.
As we shall see in Chapter 5, the above prediction of Santilli's isorelativity are indeed verified by all available experimental data. Their implications are rather deep because they imply that, e.g., light is expected to exit a star or, much equivalently, a high energy scattering region, at a frequency bigger than that of its origination, while light is expected to leave planetary atmospheres or astrophysical chromospheres at a frequency smaller than that of its origination.
The celebrated equivalence principle E = m c2 is experimentally verified only for point-like particles moving in vacuum. The isoequivalence principle expresses expected differences in excess or in defect from the conventional equivalence principle depending on said anisotropic ratio, said differences being merely due to processes of acquisition of release of energy to the medium.
3.10H. Santilli's isogravitation and its isodual
As indicated in Section 2.6, one of Santilli's most important mathematical contributions has been the geometric unification of the Minkowskian and Riemannian geometries into the Minkowski-Santilli isogeometry. This unification has evidently been done as the premise for the unification of special and general relativities. In fact, Santilli's isorelativity is unique in the sense that it incorporates both the special and the general relativity.
As indicated earlier, isotopic line elements (3.58) include as particular cases all infinitely possible (nonsingular) Riemannian line elements. Hence, Santilli first contribution in gravitation has been the construction of a universal "symmetry of gravitation", in lieu of the 20-th century "covariance".
The isominkowskian formulation of exterior gravitation is elementary. Any nonsingular Riemannian metric g(r) always admit the decomposition into the Minkowski metric m = Diag. (1, 1, 1, - c2) and a 4x4 dimensional positive-definite matrix Tgr(r) called gravitational isotopic element because it incorporates all gravitational features. Santilli then assumes for basic isounit of exterior gravitation the inverse of Tgr,
The implications of the above discovery are far reaching and affect all quantitative sciences from classical mechanics to astrophysics. To begin, the formulation avoids the Theorems of Catastrophic Inconsistencies of Section 3.9 thanks to the invariance of isogravitation under the Poincare
-Santilli isosymmetry. The same also allows an axiomatically consistent operator formulation of gravity and grand unification, the sole known to the Foundation as being consistent.
As it is well known, all distinctions between exterior and interior gravitation were eliminated in the 20th century for the evident intent of adapting nature to Einstein doctrines. This manipulation of science was done via the claim that interior problems can be reduced to a set of point-like particles under sole action at a distance, potential interactions. As an illustration of this political profile, Schwartzchild wrote two papers, one for the exterior and one for the interior gravitation. The former has been widely acclaimed in the 20th century, while the latter has been vastly ignored, evidently because the former (latter) was compatible (incompatible) with Einstein's gravitation under a serious scrutiny.
Theorem 1.1 terminates these political postures and sets the origin of macroscopic nonpotential and irreversible effects at the ultimate level of particles at short mutual distances, as a consequence of which the inequivalence of interior and exterior problems are established beyond doubt. Any dissident view should prove that light behaves in the same fashion in the exterior and interior problems, thus believing that electromagnetic waves propagates within atmospheres at the same speed as in vacuum and, additionally, light penetrates all the way to the center of astrophysical masses at the same speed as that in vacuum, which is a nonscientific posture.
For instance, the treatment of a spaceship during re-entry in atmosphere via Einstein's gravitation would be a manifest scientific politics due to the Lagrangian character of the former and the strictly non-Lagrangian nature of the latter. In particular, the resistive forces experienced by the spaceship during re-entry is set by Theorem 1.1 to occur at the level of deep mutual penetration of the peripheral atomic electrons of the spaceship and those of the surrounding atmosphere, with ensuing nonlinear, nonlocal and nonpotential interactions.
Santilli has provided the only known axiomatically correct formulation of interior isogravitation that is permitted by the complete absence of restrictions in the functional dependence of the Minkowski-Santilli isometric m*, thus allowing for the first time in scientific history to introduce in the interior problem the local speed of light, density, temperature, and other crucial features of the interior gravitational problem whose quantitative treatment is inconceivable in general relativity due to the excessive limitations of the Riemannian geometry.
For instance, consider any desired Riemannian metric for the exterior problem, e.g., for the exterior Schswartzchild's solution, with diagonal elements
A) The limit Tkk → 0, k = 1, 2, 3, directly represents the volume of the star being reduced (geometrically) to a point (because said components are the units of space dimensions; and
B) The limit I* 44 → ∞ represents the complementary occurrence for which time becomes infinite (because said component is the unity of time) or, equivalently, there is no dynamical evolution, thus preventing the release of light and mass once absorbed.
It is evident that the above features represent, by far, the most elegant and mathematical representations of gravitational collapse in history, to the Foundation best knowledge. However, as stressed by Santilli, this geometric limit is a consequence of the widespread trend in the 20the century of studying extreme interior conditions, such as gravitational collapse, with the use of exterior gravitation. By comparison, when gravitational collapse is studied more seriously via interior gravitation, it is possible to show that the collapse of a star to a point becomes impossible, while preserving the crucial features of a black holes, such as that of not releasing light or mass.
The experimental verification of Santilli isogravity is assured by the identical reformulation of the Einstein-Hilbert field equation. However, isogravitation occurs in a flat space since the Minkowski-Santilli isospace is locally isomorphic to the minkowski space and its curvature is null. This confirms the viewpoint expressed in Chapter 1 according to which the Riemannian formalism provides a very elegant mathematical representation of data, but space cannot be curved in a real sense because curvature cannot explain the weight of stationary bodies, the free fall of bodies along a straight radial line, the bending of light (that is a Newtonian event), and other features.
Alternatively, Santilli has established beyond doubt that the continued insistence on space as being actually curved directly causes: the activation of the Theorems of Catastrophic Inconsistencies; the mandatory need to revise quantum electrodynamics (Section 2.4); the impossibility of reaching a consistent operator form of gravity; the impossibility of achieving a serious grand unification of electroweak and gravitational interactions; and other shortcomings of historical proportions.
3.10I. Santilli's Lie-admissible geno- and hyper-relativities and their isoduals
As indicated in Chapter 1, Santilli considers irreversibility a fundamental feature of nature originating at the ultimate particle level in view of Theorem 1.1. Isorelativity is structurally reversible and, therefore, it is considered a mere preparatory step toward more fundamental relativities.
It should be indicated that isorelativity has the capability of representing irreversibility via time-dependent isotopic elements T(t, r, p, E, ...) = T†(t, ... ) in such a way that T(t, r, ...) ≠ T(- t, ...). However, this is a somewhat limited representation of irreversibility. In fact, isorelativity was primarily constructed to characterize closed-isolated composite systems that are stable, such as protons, thus being reversible in time, yet possessing non-Hamiltonian internal effects represented with the isounit.
The achievement of a relativity truly capable of representing irreversibility required Santilli to construct his Lie-admissible genomathematics and its multi-valued hyper-extension, that are structurally irreversible in the sense that they are irreversible for all possible reversible Hamiltonians. Once such a mathematics was available, new relativities followed, today known as Santilli geno- and hyper-relativities for matter and their isoduals for antimatter. We regret our inability to outline these broader relativities to prevent a prohibitive length, as well as a substantial increase in complexity of thought, realization and verification.
3.10J. Isotopic reconstruction of exact spacetime symmetries when conventionally broken
The physics of the 20th century saw a rather popular interest in "symmetry breakings" for both spacetime and internal symmetries. Santilli has shown that such "breakings" are due to the use of insufficient mathematics because, when the problem at hand is treated with a more appropriate mathematics, the symmetry is reconstructed exactly and no breaking occurs.
The reconstruction of the exact SU(2)-isospin and SU(3)-color symmetries will be reviewed in Chapter 5. Here we indicate Santilli's mechanism for the exact symmetry reconstruction for the case of spacetime symmetries. Consider the perfect sphere of radius 1 defined on the Euclidean space over the reals R and its known symmetry under the rotational group SO(3),
The reconstruction of the exact Lorentz symmetry when believed to be broken is intriguing. The admission of a locally varying speed of light causes the loss of the light cone within physical media. However, as it is the case for the isosphere, the mutations of spacetime coordinates occur under a joint inverse mutation of the related unit. This process yields Santilli's light isocone which is the perfect cone in isospace over isofield, but whose projection on conventional space over the conventional field yields a highly mutated cone whose shape changes in time. The preservation of Einstein's axioms as well as the local isomorphism of the Lorentz-Santilli and the conventional Lorentz symmetry are crucially dependent on the exact reconstruction of the light cone on isospace over isofields with the consequential exact reconstruction of the Lorentz symmetry.
The reconstruction of exact discrete spacetime symmetries is handled in essentially the same manner, thus voiding the 20th century belief that spacetime symmetries are broken.
A. P. Mills,
Hadronic J. vol. 19, 77-96 (1996)
R. M. Santilli,
Ukraine Academy of Sciences (1994)
R. M. Santilli,
Springer (2006)
J. Dunning-Davies,
to be completed and uploaded
R. M. Santilli, Nuovo Cimento Vol. 51, 570-576 (1967).
where AB is the conventional associative product, and p, q, p ± q are non-null parameters or functions. In particular, Santilli stressed in the 1967 paper that that his product (A, B) is jointly Lie-admissible (namely, (A, B) - (B, A) is Lie) and Jordan admissible (namely, (A, B) + (B, A) is Jordan),
that, for p = 1 and q = 1 - ε/(∂H(r, p)/∂r), Eqs. (3.31) are approximated into the form
with nonunitary time evolution of an observable Q in the finite and infinitesimal forms
thus regaining a consistent algebra in the brackets of the time evolution, while representing, for the first time, nonconservative and irreversible systems. The lack of totally antisymmetric character of the brackets then characterize the time rate of variation of the energy
as well as of other quantities.
NONCANONICAL AND NONUNITARY THEORIES (1978)
Schroedinger's equations (for h-bar = 1)
and the canonical commutation relations
A most dominant property needed for the majestic consistency is that the time evolution operator U(t) constitutes a unitary transformation when formulated on a Hilbert space over the field of complex numbers,
The corresponding property for the classical time evolution is that of constituting a canonical transformation, that also preserves the unit.
But the unit I = Diag. (1, 1, 1) generally represents in an abstract way units actually used in experiments, such as I = Diag. (1 cm, 1 cm, 1 cm). Consequently, the unitary character of the time evolution law of quantum mechanics implies the preservation over time of the basic units of measurements,
Additionally, a quantity that is an observable (Hermitean) at the time t = 0 remains observable at all subsequent times,
Also, if quantum mechanics yields a given numerical prediction, e.g., 57.72 MeV, at a given time, the theory maintains the same numerical prediction under the same conditions at all subsequent times,
Finally, the unitarity of the time evolution permits the verification of causality and other physical laws. As a result, quantum mechanics has the majestic feature of preserving over time the units of measurements, the observability of physical quantities, the numerical predictions under the same conditions, causality and other laws. A corresponding physical consistency holds for classical Hamiltonian formulations.
when formulated with the mathematical methods of unitary theories (conventional fields, spaces, functional analysis, differential calculus, etc.) do not preserve said mathematical methods over time, thus being afflicted by catastrophic mathematical inconsistencies, and do not preserve over time the basic units of measurements, Hermiticity-observability, numerical predictions and causality, thus suffering of catastrophic physical inconsistencies.
Consequently, said theories lose the base field at subsequent times with the consequential catastrophic collapse of their entire mathematical structure.
Similarly, nonunitary theories do not generally preserve observability over time, because they do not preserve Hermiticity over time in view of the Lopez lemma for which the known Hermiticity condition
is mapped under a nonunitary transform into the form
due to the general lack of commutativity of H' and T, H' T ≠ T H'.
Finally, one of Santilli's graduate students has proved that theories with a nonunitary time evolution violate causality laws and have other catastrophic inconsistencies. Santilli then concludes by saying Nonunitary theories formulated with the mathematics of unitary theories have no mathematical or physical value of any type.
In fact, these theories violate the superposition principle and, consequently, cannot be consistently applied to composite states.
where Q ⊗ H is nonassociative,
because these theories cannot admit any left and/or right unit, thus lacking the definition over a field, prohibit any measurements, lack any consistent exponentiation to reach finite transforms and have other catastrophic inconsistencies (the scholar not familiar with these occurrences should inspect in detail Chapter 2, see the insistence on conventional, or iso- and geno-associative enveloping algebras, and attempt their nonassociative generalizations).
A. Jannussis, R. Mignani and R. M. Santilli,
Ann. Fond. L. De Broglie, Vol. 19, pages 371-389 (1993)
A. Jannussis and D. Skaltzas,
Ann. Fond. L/. De Broglie Vol. 18, pages 137-154 (1993)
Lopez's Lemma on the general lack of preservation of Hermiticity-Observability under nonunitary time evolutions originated in the papers
J. F. Lopez,
Hadronic Journal Vol. 16, pages 429-457 (1993)
D. F. Lopez,
In "Symmetry Methods in Physics", , Vol. 1, Joint Institute for Nuclear Research, Dubna, Russia (1994)
R. M. Santilli,
Modern Phys. Letters Vol. 13, 327-335 (1998)
R. M. Santilli,
Intern. J. Modern Phys. Vol. 14, pages 3157-3206 (1999)
Ruggero Maria Santilli
Galilean Electrodynamics, Summer 2006, p. 43-79 (2006)
R. M. Santilli,
Found. Phys. Vol. 32, 1111-1140 (2002)
Ruggero Maria Santilli
Nuovo Cimento B Vol. 121, p. 443-595 (2006)
where the index of refraction n = n4 is extended to all components because generated by the mere application of Lorentz transforms or other symmetrization processes.
with isotopic element and isounit the expressions
Santilli then:
where † evidently represents transposed for real values matrices; and
the isoproduct
the isoexponentiation to the right and to the left for a given Lorentz generator J with related parameter w
and the consequential isotopy of the finite Lorentz transformations of a physical quantity Q(w)
All remaining needed isomathematics can be constructed in the same elementary way. The isodual formalism for antimatter is derived via the simple isodual transform (2.9) applied to the totality of the isotopic methods (see Section 2.7 for formal treatments)
because the above transform does not leave invariant the basic isounit.
with consequential lack of invariance of the isoproduct
The above lack of basic invariances activates Theorem 3.9A with catastrophic mathematical and physical inconsistencies that should have been expected due to the mixing of isotopic methods formulated on isospaces over isofields with conventional transformations formulated on conventional spaces over conventional fields.
It is easy to see that Santilli's isotopic formalism is indeed invariant under the above isocanonical or isounitary transforms. In fact, we have the invariance of the isounit
Similarly, we have the invariance of the isoproduct
namely, the isotopic element T remains unchanged. The invariance of all remaining operations then follow and Theorem 3.9A is bypassed.
and comprises: the six-dimensional Lorentz-Santilli isosymmetry SO*6(3.1); the four-dimensional isotranslations T
Lie-Santilli isocommutation rules in terms of isoproduct (2.26),
Casimir-Santilli isoinvariants
and isotransforms;
2) Isoboosts here presented for motion in the conventional (3,4) plane
where v is the speed along the third axis;
4) Isotopic transform
under which isoline element (3.58) remains indeed invariant.
where r = ( rk), k = 1, 2, 3, r4 = t, and rk2 = (rk)2.
Since all spacetime symmetries have important physical applications, the same holds for the isotopic symmetry. In fact, the new symmetry allowed Santilli to reach a basically new grand unification of electroweak and gravitational interactions, as we shall see later on.
ISOAXIOMS II: The isorelativistic addition of speeds within physical media is set by the law
ISOAXIOM III: Within physical media, time dilation, length contraction, and variation of mass with speed follow the isotopic laws
AXIOM IV: Within physical media the variation of light frequency with speed follows the Doppler-Santilli isotopic law, here written for simplicity for 90o aberration angle as well as in expansion to first order
ISOAXIOM V: Within physical media the energy equivalence of the mass follows the isotopic law
COMMENTS: Note that the maximal causal speed is set by the geometry of the medium, namely, by the difference between the space and time characteristic quantities representing the anisotropy. As such, Vmax can be bigger, equal or smaller to the speed of light in vacuum. In particular, for isotropic media, Vmax = c.
The entire formalism of the Minkowski-Santilli isogeometry then applies, including the identical reformulation of the Einstein-Hilbert field equations, although completed with sources as in Section 3.4.
Then, a simple lifting of such an exterior metric to the interior problem is given by the following forms where the characteristic quantities depend on local coordinates, r, density μ, temperature τ, etc.,
Following, and only following a more credible representation of interior gravitational problems, Santilli presented gravitational singularities as the zeros of the time component of the gravitational isotopic element or the infinities of the space components of the gravitational isounit,
as one can verify via Eq. (3.101). By recalling the physical meaning of the characteristic quantities, one can then see the direct geometric representation of the singularity as follows:
Suppose that the above perfect sphere is elastic and experiences a deformation into an ellipsoid of the type
It is evident that, when continued to be defined on the Euclidean space over the reals, the above deformation causes the breaking of the rotational symmetry SO(3). Santilli principle of reconstruction of the exact rotational symmetry is based on the deformation of the line element
while jointly submitting the basic unit of the Euclidean space I = Diag. (1, 1, 1) to the inverse deformation
It is then easy to see that the definition of the deformation on the Euclid-Santilli isospace with isounit I* recovers a perfect sphere called isosphere,
In fact, if one semiaxis is deformed of the amount 1/nk2, but the corresponding unit is deformed of the inverse amount nk2, the numerical value of the semiaxes on isospace over isofields remains 1, with the resulting exact isosymmetry SO*(3). But the latter symmetry is isomorphic to the conventional one SO(3), thus yielding an exact reconstruction of the rotational symmetry, merely formulated with a more appropriate mathematics.
Figure 3.8. The understanding of Santilli isorelativity and its particular realization as isogravitation, requires a knowledge of the light isocone, which is the perfect light cone, but defined on the Minkowski-Santilli isospace over Santilli's isonumbers. This deceptive simplicity hides in reality very deep implications. To begin, the projection of the isocone in the conventional spacetime characterizes a locally varying speed of light with consequential highly deformed cone. Hence, Santilli's isotopies reconstruct on isospaces over isofield the exact light cone when no longer applicable in our spacetime. This exact reconstruction is at the foundation of the preservation of the axioms of special relativity for dramatically broader physical conditions, as well as the reconstruction of the exact Lorentz symmetry when popularly believed to be broken. Additionally, Santilli's isocone permits a direct geometrization of gravitation without curvature. In fact, the deviations from the perfect light cone can be due to gravitation, and be characterized by the components of, e.g., Schwartzschild's metric (3.101). But each of these deviations is referred to a unit that is its inverse. Ergo, all Riemannian metrics can be reduced to Santilli's isocone with implications, as we shall see, way beyond conventional gravitational studies, such as for the scattering theory, nuclear events, and others, all permitted by the elimination of curvature.
3.10K. Experimental verifications
In the arena of its applicability (dynamics within physical media or particles in conditions of deep mutual penetration), Santilli isorelativity has experimental verifications in classical physics, particle physics, nuclear physics, supuercondiuctivity, chemistry, astrophysics and cosmology (see the literature for quantitative treatments). Some of these verifications will be outlined in Section 3.12, 3, and chapter 5.
An illustrative experimental verification of isorelativity in classical physics is given by electromagnetic waves propagating in water. In this case, the speed of light is given by C = c/n4, but the medium is homogeneous and isotropic, as a result of which Vmax = c, thus allowing electrons to travel faster than the local speed of light and verifying causality, as well as the isorelativistic sum of speeds. A similar case occurs for Newton's diffraction of light, and numerous other cases in which there is a deviation of the speed of light from that in vacuum.
An illustrative experimental verification in particle physics is given by the Bose-Einstein correlation outlined in Chapter 5, and other relativistic events in particle physics conventionally treated via the use of ad hoc parameters fitted from the data (and then claim that special relativity is exactly valid!). These parameters are eliminated in isorelativity and replaced with measurable quantities, such as size of particles, their density, etc. The most important verification in particle physics is the numerically exact representation of all characteristics of neutrons in their synthesis from protons and electrons as occurring in stars, which synthesis, as indicated in Chapter 1, admits no treatment at all via special relativity (see Chapter 5 for details).
An illustrative experimental verification in nuclear physics is given by nuclear magnetic moments that can be solely represented in an exact way via a deformation of charge distributions of protons and neutrons when members of a nuclear structure. These deformations are absolutely impossible for special relativity, but readily admitted by its covering isorelativity. Numerous other verifications also exist in nuclear physics (see Chapter 5 for details).
An illustrative experimental verification in astrophysics is given by the exact representation of dramatically different redshifts of galaxies and quasars when physically connected according to gamma spectroscopy, which representation is permitted by Santilli isoredshift indicated above. For additional verifications, the serious scholar is suggested to consult the specialized literature.
Unfortunately,we have an unreassuring situation in the experimental verification of Einsteinian doctrines for conditions beyond those of their original conception. As Santilli puts it:
Following some fifty years of active research on fundamental open problems, it is my documented view that theories in physics are nowadays established by organized academic consensus and definitely not by a serious scientific process.
In fact, the consideration, let alone the conduction, of systematic experimental tests of Einsteinian theories, under conditions they were not intended for, is nowadays impossible at any major physics laboratory around the world. When limited tests are conducted, Einsteinian doctrines are studiously recovered via the use of arbitrary parameters and their fit from experimental data, while in reality these arbitrary parameters are a direct measure of the "deviations" from the indicated doctrines (see The Bose-Einstein correlation and other tests of Chapter 6).
These unreassuring condition establish the existence of a real scientific obscurantism at the beginning of the third millennium originating from protracted complete impunity by academic interests guaranteed by lack of societal control under full support of governmental agencies funding the research. The unreassuring character is that new the conception and development of new clean fuels and energies so much needed by society basically depend on "deviations" from Einsteinian doctrines. In the final analysis, all possible energies that could be conceived with Einsteinian doctrines were fully identified half a century ago and they all turned out to be environmentally unacceptable.
Therefore, the solution of the increasing environmental problems afflicting our planet cannot be even initiated until responsible societies impose systematic experimental tests on the "limitations" of Einsteinian theories. The serious reader serious interested in knowledge, rather than in myopic personal gains, should never forget that time reversal invariant theories, such as Einsteinian doctrines, cannot credibly be assumed as being exact until the end of time for structurally irreversible processes, such as all energy releasing events.
3.10L. Original literature
Following decades of work, Santilli first proposed his Lie-admissible covering of Galilei and special relativities, today called genorelativities, in the following 200 pages memoir of 1978 with a full identification of the isotopic particular cases, today called isorelativity,
On a possible Lie-admissible covering of Galilei's relativity in Newtonian mechanics for nonconservative and Galilei form-noninvariant systems
R. M. Santilli,
Hadronic J. Vol. 1, 223-423 (1978)
and then continued the study in more details in the following two monographs of 1978 and 1982
"Lie-Admissible Approach to the Hadronic Structure, I: Non applicability of the Galilei and Einstein Relativities,"
R. M. Santilli,
Hadronic Press (1978)
"Lie-Admissible Approach to the Hadronic Structure, II: Coverings of the Galilei and Einstein Relativities"
R. M. Santilli,
Hadronic Press (1982)
Systematic studies on isorelativity were initiated in 1983 via the following papers: 1) The first isotopies of the Lorentz symmetry on scientific record at the classical level in the paper of 1983 that includes the first known universal invariance of Riemannian line elements
Lie-isotopic lifting of special relativity
for extended deformable particles
R. M. Santilli,
Lettere Nuovo Cimento Vol. 37, 545-555 (1983)
2) The first isotopies of special relativity at the operator level also in 1983
Lie-isotopic lifting of unitary symmetries and
of Wigner's theorem for extended deformable particles,
R. M. Santilli,
Lettere Nuovo Cimento Vol. 38, 509-521 (1983)
3) The first known isotopies of the rotational symmetries were presented in the following two papers of 1985 that were written before the preceding two but were rejected by various journals via pseudo-reviews reported in the first paper
Lie-isotopic liftings of Lie symmetries, I: General considerations,
R. M. Santilli,
Hadronic J. Vol. 8, 25-35 (1985)
Lie-isotopic liftings of Lie symmetries, II: Lifting of rotations,
R. M. Santilli,
Hadronic J. Vol. 8, 36-51 (1985)
4) The first isotopy of SU(2) spin appeared in the following papers of 1993 and 1998 (the second presenting intriguing application to Bell's inequality, local realism and all that)
Isotopic lifting of SU(2)-symmetry with
application to nuclear physics,
R. M. Santilli,
JINR rapid Comm. Vol. 6. 24-38 (1993)
Isorepresentation of the Lie-isotopic SU(2) algebra with application to nuclear physics and local realism,
R. M. Santilli,
Acta Applicandae Mathematicae Vol. 50, 177-190 (1998)
5) A detailed study isotopy of the Poincare' symmetry as the universal invariance for all spacetimes with signature (+, +, +, -) was published in 1993
Nonlinear, nonlocal and noncanonical isotopies of the Poincare' symmetry,
R. M. Santilli,
Moscow Phys. Soc. Vol. 3, 255-280 (1993)
6) the first known isotopies of the spinorial covering of the Poincare' symmetry (with momentous implications in particle physics identified in the next section) appeared in the following two papers of 1993 and 1995
Recent theoretical and experimental evidence on the apparent
synthesis of neutrons from protons and electrons,
R. M. Santilli,
Communication of the JINR, Dubna, Russia, Number E4-93-252 (1993)
Recent theoretical and experimental evidence on the apparent
synthesis of neutrons from protons and electrons,
R. M. Santilli,
Chinese J. System Engineering and Electronics Vol. 6, 177-199 (1995)
7) The unification of special and general relativity into isorelativity was systematically studied in the following paper of 1998
Isominkowskian geometry for the gravitational treatment of matter and its isodual for antimatter,
R. M. Santilli,
Intern. J. Modern Phys. D Vol. 7, 351-407 (1998)
The reading of the following additional papers is instructive for the serious scientist serious on science
Lie-isotopic generalization of the Poincare' symmetry, classical formulation
R. M. Santilli,
ICTP preprint # IC/91/45 (1991)
published in "Santilli's 1991 Papers at the ICTP", International Academic Press (1992)
Galilei-isotopic relativities
R. M. Santilli,
ICTP preprint #
published in "Santilli's 1991 Papers at the ICTP", International Academic Press (1992)
Galilei-isotopic symmetries
R. M. Santilli,
ICTP preprint # IC/91/263 (1991)
published in "Santilli's 1991 Papers at the ICTP", International Academic Press (1992)
Rotational isotopic symmetries
R. M. Santilli,
ICTP preprint # IC/91/261 (1991)
published in "Santilli's 1991 Papers at the ICTP", International Academic Press (1992)
The first systematic presentation of the isotopies of Galilei and Einstein's relativities with the experimental proposal to verify the isoredshift appeared in the following monographs of 1991,
"Isotopic Generalization of Galilei and Einstein Relativities",
Volume I: "Mathematical Foundations"
R. M. Santilli,
Hadronic Press (1991)
"Isotopies of Galilei and Einstein Relativities"
Vol. II: "Classical Foundations"
R. M. Santilli,
Hadronic Press (1991)
The first verification of the isodoppler shift of Santilli's isorelativity predicted in the preceding two volumes was done in 1992 by R. Mignani via the numerical interpretation of dramatically different redshift of quasars when physically connected to associated galaxies
Quasar redshift in iso-Minkowski space
R. Mignani.
Physics Essays Vol. 5, 531-535 (1992)
The first studies on the direct universality of Santilli's isorelativity for all possible spacetimes with signature (+, +, +, -) are given by the following papers
Direct universality of isospecial relativity for
photons with arbitrary speeds,
R. M. Santilli,
in "Photons: Old problems in Light of New Ideas"
V. V. Dvoeglazov Editor
Nova Science (2000)
Direct universality of the Lorentz-Poincare'-Santilli
isosymmetry for extended-deformable particles,
arbitrary speeds of light and all possible spacetimes
J. V. Kadeisvili,
in "Photons: Old problems in Light of New Ideas"
V. V. Dvoeglazov Editor
Nova Science (2000
Universality of Santilli's iso-Minkowskian geometry,
A. K. Aringazin and K. M. Aringazin,
in "Frontiers of Fundamental Physics"
M. Barone and F. Selleri, Editors
Plenum (1995)
The latest study on the Lie-admissible covering of special relativity for irreversible systems was presented in the memoir published by the Italian Physical Society
Lie-admissible invariant representation of irreversibility for matter and antimatter at the classical and operator level
Ruggero Maria Santilli
Nuovo Cimento B Vol. 121, p. 443-595 (2006)
Systematic studies on both the Lie-isotopic and Lie-admissible coverings of special relativity appeared in the two memoirs of 1995 with the update below of 2008
"Elements of Hadronic Mechanics", Vol. I: "Mathematical Foundations"
R. M. Santilli
Ukraine Academy of Sciences (1995)
"Elements of Hadronic Mechanics"
Vol. II: "Theoretical Foundations"
R. M. Santilli,
Ukraine Academy of Sciences (1995)
Hadronic Mathematics, Mechanics and Chemistry, Volume III: Iso-, Geno-, Hyper-Formulations for Matter
and Their Isoduals for Antimatter
R. M. Santilli,
International Academic Press (2008)
For various independent reviews of Santilli's iso- and geno-relativities interested scholars may consult the following monographs
"Santilli's Lie-Isotopic Generalization of Galilei and Einstein Relativities"
A. K. Aringazin, A. Jannussis, F. Lopez, M. Nishioka and B. Veljanosky,
Kostakaris Publishers, Athens, Greece (1991)
"Mathematical Foundation of the Lie-Santilli Theory"
D. S. Sourlas and G. T. Tsagas,
Ukraine Academy of Sciences 91993)
"Santilli's Isotopies of Contemporary Algebras
Geometries and Relativities"
J. V. Kadeisvili,
Ukraine Academy of Sciences
Second edition (1997)
3.11. HADRONIC MECHANICS (1967)
3.11A. Foreword
Santilli's conception, construction, development, experimental verification, and industrial applications of hadronic mechanics, with its diversification in mathematics, physics, chemistry and biology, constitutes, without doubt, a historical scientific achievement, mostly unprecedented if one considers the novelty and variety of the needed studies by one single mind, from pure mathematics to industrial applications.
Nowadays (October 2008), hadronic mechanics constitutes a rather vast body of disciplines ranging from various coverings of Newtonian mechanics all the way to various corresponding coverings of second quantization, including as particular cases conventional classical and operator conservative formulations.
As we shall see in Chapters 4 and 5, hadronic mechanics was original conceived for: 1) Quantitative treatments of the synthesis of neutrons from protons and electrons as occurring in stars, that cannot be treated via quantum mechanics 2) Quantitative studies on the possible utilization of the inextinguishable energy contained inside the neutron; 3) The study of new clean energies and fuels that cannot even be conceived with the 20th century doctrines; and other basic advances. The implementation of these main objectives required the conception, construction and test of a sequence of branches for the treatment of matter in conditions of correspondingly increasing complexity, plus all their isoduals for antimatter.

Figure 3.9. Classification of hadronic mechanics into its various classical and operator branches as presented by Santilli in his volumes in the field.
Evidently, we can review here only the rudiments of hadronic mechanics and refer the serious scholar to a serious study of the literature made available in free pdf downloads. In particular, we shall provide the rudiments of the isotopic branch of hadronic mechanics and merely indicate the remaining geno-, hyper- and isodual branches. It should be indicated that the primary aim of this section is the identification of Santilli's original discoveries in the field. For all numerous subsequent contributions by various researchers around the world, interested scholars are suggested to consult the
General Bibliography on Santilli Discoveries
3.11B. Historical notes
The period 1965-1967
The birth of hadronic mechanics can be traced back to Santilli's Ph. D. studies in theoretical physics at the Depart of Physics of the University of Torino, Italy, with particular reference to the following papers
Embedding of Lie-algebras in nonassociative structures
R. M. Santilli, Nuovo Cimento Vol. 51, 570-576 (1967).
An introduction to Lie-admissible algebras
R. M. Santilli,
Supplemento al Nuovo Cimento Vol. 6, pages 1225-1249 (1968)
Dissipativity and Lie-admissible algebras
R. M. Santilli,
Meccanica, Vol. 1, pages 3-11 (1969)


On mathematical grounds, being an applied mathematician by instinct, Santilli recognized that quantum mechanics is structurally dependent on Lie theory that characterizes the infinitesimal time evolution of a (Hermitean) operator Q, i dQ/dt = [Q, H] = QH - HQ via the Lie product [Q, H] (H being the usual Hermitean Hamiltonian representing the total energy), and the finite time evolution via the Lie transformation group Q(t) = exp(Hti)Q(0)exp(-itH), As a pre-requisite to generalize quantum mechanics, Santilli searched for a covering of Lie's theory, namely, a generalization such to maintain a well defined Lie content, a mathematical feature necessary for the broader physical theory to admit quantum mechanics as a particular case.
For this purpose, Santilli proposed the first known mutations of Lie algebras (today also known as "deformations" ) with product
where λ, μ, λ ± μ are non-null scalars. It was then simple for Santillio to discover the following generalizations of Heisenberg's time evolution in their infinitesimal and finite forms
with corresponding classical counterparts (see Section 3.8). Quantum mechanics and its Lie structure were then recovered identically and uniquely for the particular case λ = μ = 1.
Because of his keen sense of scientific ethics, Santilli delayed the publication of the 1967-1968 papers for over one year to identify at least some prior literature for due quotation. In so doing, he spent months of search in mathematical libraries, not only in Italy but also in other countries, looking for some mathematical paper treating the algebra with his product (A, B).
After such a protracted search, Santilli finally discovered a 1947 paper by the American mathematician
A. A. Albert presenting the definition without concrete examples of the notions of Lie-admissible and Jordan-admissible algebras. An algebra U with elements a, b, c, ... and abstract product ab was called by Albert Lie-admissible when the attached antisymmetric algebra U- with product [a, b] = ab - ba is Lie. Albert called the sam algebra Jordan-admissible when the attached symmetric algebra U+ with product {a, b} = ab + ba is Jordan.
Santilli immediately recognized that his product (A, B) is indeed Lie- and Jordan-admissible
and adopted Albert's definition, particularly in view of the possibility of realizing "Jordan's dream" that his celebrated algebras would see physical applications, although not in quantum mechanics as well known, but within the context of a covering mechanics.
Santilli then spent additional months of search in mathematics libraries to identify any papers treating Albert's Lie- and Jordan-admissible algebras. In this way, he located only two additional short notes published in rare mathematics journals treating Albert's definition although without any concrete realization.
Following such an extensive search that is rather unusual these days in the physics community, let alone for a physicist to conduct protracted searches in pure mathematical journals, Santilli released for publication his 1967-68 papers with all pre-existing literature properly quoted, which papers present the first known realization in both mathematical and physical literature of a jointly Lie- and Jordan-admissible algebra.
On physical grounds, Santilli had understood during his Ph. D. studies that quantum mechanics is a theory structurally reversible over time and that the characterization of the conventional conservation law, such as that of the energy H, is due to the totally antisymmetric character of the Lie product for which i dH/dt = [H, H] = HH - HH = 0.
As recalled in Section 1.1, D. Santilli studied Lagrange's original works and learned in this way the necessity of achieving an irreversible generalization of quantum mechanics. as an operator counterpart of the "true Lagrange and Hamilton equations," those with external terms characterizing precisely the irreversibility of the physical world (Section 1.1).
But all known Hamiltonians (that is all 20th century interactions) are reversible over time. The representation of irreversibility then left Santilli with no other option than that of generalizing the Lie product into a non-antisymmetric form as a condition for an operator representation of
nonconservative irreversible systems.
It is evident that Santilli Lie- and Jordan-admissible product does indeed verify the latter condition because, in general, (A, B) - (B, A) ≠ 0. Therefore, he submitted his covering equations (109)-(112) for the representation of open nonconservative and irreversible systems, a central feature that is s fully valid today.
The period 1978-81
In 1967 Santilli moved to the U. S. A. for a one year research position at the University of Miami, Coral Gables, Florida, funded by NASA. During that time, he applied for a junior position in virtually all U. S. physics and mathematics departments on grounds of his studies on Lie-admissible and Jordan-admissible algebras. However, these algebras were unknown in both the mathematics and physics of the late 1960s.
He then accepted a position at the Department of Physics of Boston University partially funded by the U. S. Air Force (for which support he acquired the U. S. citizenship), and turned himself to publications that, in his words, are typical Phys. Rev. papers nobody quotes or cares for, some of which have been outlined in Sections 3.4, 3.5, 3.6. During that period, Santilli continued to study Lie-admissible and Jordan-admissible theories without any publication in the field for about a decade.
In 1977 Santilli joined the Lyman Laboratory of Physics of Harvard University following an invitation by the DOE for grant number DE-ACO2-80ER-10651.A00, for which Santilli was transferred at Harvard's Department of Mathematics. At that time, Santilli published the following two memoirs with the formal proposal to construct hadronic mechanics including its central dynamical equations, memoirs hereon referred to as the 1978 Original Memoirs I and II
On a possible Lie-admissible covering of Galilei's relativity
in Newtonian mechanics for nonconservative and Galilei form-noninvariant systems
R. M. Santilli, Hadronic J. Vol. 1, 223-423 (1978)
Need of subjecting to an experimental verification the validity within a hadron of Einstein special relativity and Pauli exclusion principle
R. M. Santilli, Hadronic J. Vol. 1, 574-901 (1978)
The first memoir presents a detailed mathematical study of Lie-admissible and Jordan-admissible algebras with their Lie-isotopic and Jordan-isotopic particularizations, and the second memoir presents the basic equations of hadronic mechanics with first applications and illustrations.

Figure 3.11. A view of the Science Center of Harvard University housing at the third floor Harvard's Department of Mathematics were Santilli reached in 1977-1981 the main formulation of hadronic mechanics.
In essence, Santilli recognized that his Lie-admissible time evolution (110) is nonunitary, UU† ≠ I, as a necessary condition to exit from the class of unitary equivalence of quantum mechanics. Consequently, he applied a general nonunitary transformation to his parametric product (109), and achieved in this way the broader product today known as Santilli general Lie-and Jordan-admissible product
where R, S and R ± S are now non-null operators.
Santilli also discovered that his algebra with product (A, B)* is the most general known algebra, in the sense of admitting as particular case all infinitely possible algebras known in mathematics (characterized by a bilinear composition verifying the left and right scalar and distributive laws), including Lie algebras, Jordan algebras, flexible algebra, supersymmetric algebras, etc. Additionally, Santilli discovered that his algebras remain jointly Lie-and Jordan-admissible under all possible (nonsingular) nonunitary transforms (although the operator R and S would change).
Following the achievement of these remarkable results in the Original Memoir I, it was rather natural to propose in the Original memoir II (see, Eqs. (4.15.34), page 746) equations today known as Santilli Lie- and Jordan-admissible dynamical equations that are at the foundation of hadronic mechanics, here presented in the following infinitesimal and finite forms,
under the condition for physical consistency (derived from time reversal) that R = S†.
In the same Original memoir II (see the 1978 Memoir II, Eqs. (4.15.49), page 752), Santilli identified the fundamental Lie-isotopic equations of hadronic mechanics as a particularization of the Lie-admissible equations, here also presented in the following infinitesimal and finite forms,
under the condition olf the operator T being positive definite, T = T† > 0.
Eqs. (114), (115) were proposed for the operator representation of open irreversible systems, again in view of the lack of antisymmetric character of the basic product (A, B)*, while Eqs, (116), (117) were proposed for closed-isolated systems with potential and nonpotential internal forces verifying conventional total conservation laws from the antisymmetric character of the product for which i dH/dt = HTH - HTH = 0. It was clearly identified in the Original Proposals that the Hamiltonian represents all action-at-a-distance potential interactions, while the operators R. S and T are the operator counterparts of Lagrange's and Hamilton's external terms since they too represent contact nonpotential interactions.
In the same memoirs of 1978 Santilli proposed the Birkhoffian-admissible mechanics as classical counterpart of the Lie-admissible equations and Birkhoffian mechanics as counterpart of the Lie-isotopic particularization, although this Birkhoffian classical counterpart had to be reformulated later on due to the impossibility of achieving a consistent quantization.
Santilli's proposal of 1978 propagated quite rapidly all over the world (despite the lack of emails at that time), and received numerous authoritative supports, such as those by Nobel Laureates C. N. Yang and I. Prigogine, distinguished physicists such as S. Okubo, S. Adler, M.S. Froissart, and others, as well as known philosophers of science such as K. Popper (who praised Santilli's proposal in the preface of his last book). A feverish research was then initiated on the construction of hadronic mechanics in the necessary aspects and operational details by various mathematicians, theoreticians and experimentalists the world over, as listed in
General Bibliography on Santilli Discoveries.
Thanks to his mathematical knowledge, Santilli initiated in 1979 the representation theory of Lie-admissible algebras. Let |ψ) be the module of a Lie-representation, e.g. a ket belonging to a Hilbert space with right associative action H |ψ). In this case the bimodular character is trivial because the action to the left is antiisomorphic to that to the right, H |ψ) = - (ψ| H, H = H†.
For the case of Lie-admissible algebras with brackets (3.109), Santilli needed an isotopic action to the right H S |ψ) that is inequivalent to the to the left (ψ| R H, resulting in a new structure he called an genobimodule or Lie-admissible bimodule. These studies provided the first known Lie-admissible generalization of Schroedinger's equation and their Lie-isotopic counterpart
where, in accordance with our notations of Section 2.8, the indices f and b stands for "forward" and "backward" actions, respectively. The above realizations were subsequently studied by the physicists: R. Mignani in 1981; the mathematician H. C. Myung and Santilli in 1982; Mignani, Myung and Santilli in 1983; and others (see the indicated General Bibliography).
The period 1982-1989
In 1982, Santilli left Harvard University to assume the position of President of the Institute for Basic Research, an independent institution comprising about 120 mathematicians, theoreticians and experimentalists with dual associations to other institutions around the world. To house the new Institute, the Real Estate Trust of the Santilli family purchased a Victorian house located within the compound of Harvard University, where an intense research activity was conducted until 1989 under partial financial support by the DOE.

During that period, a large number of papers, monographs and conference proceedings then followed authored by numerous scientists the world over for an estimated number of over 20,000 pages of printed research. However, with the passing of the years Santilli was more and more dissatisfied for the status of hadronic mechanics because the Lie-admissible character of the theory was indeed preserved by unitary and nonunitary transforms, but the theory was not invariant over time, thus predicting different numerical values under the same conditions at different times, and activating the Theorems of Catastrophic inconsistencies of Nonunitary Theories of Section 3.9.
The period 1990 to present
In 1990, the Institute for Basic Research was tranfer from Cam,bridge MA, to Palm Harbor, FL, where it still operates to this day (Spring 2009). The main technical issue addressed during this period is that, by the early 1990s hadronic mechanics was still incomplete due to the lack of a Lie-admissible and Lie-isotopic generalization of the fundamental equation for the linear momentum and its action on a wavepacket (with h/2π = 1),
As Santilli recalls: The achievement of the invariance over time of hadronic mechanics has been one of the most distressing and time consuming research problems I ever faced because I knew that quantum mathematics had to be entirely lifted into hadronic mathematics for any consistent treatment. This required the isotopic and then the genotopic liftings of all branches of quantum mechanics and all its mathematics.
By the early 1990s "all" main aspects of quantum mathematics I was aware of had indeed been lifted, including numbers, vector and metric spaces, geometries, algebras, groups, representation theory, topology, etc. Nevertheless, the invariance of hadronic mechanics remained elusive and, most frustratingly, the lifting of the linear momentum into forms compatible with the Lie-isotopic and Lie-admissible formulations escaped continuous efforts for years by myself as well as several researchers in the field.
I remember that in early 1990s I used to control again and again all isotopic and genotopic liftings of quantum mechanics and could not identify the flaw causing lack of invariance and had no clue on how to lift the linear momentum. This was quite distressing because hadronic mechanics was not a complete theory without a consistent formulation of eigenvalue equation for the linear momentum. Above all, without such a formulation, no experimental verification could be seriously studied.
Finally, the teaching of the founders of physics came to my help. In 1994, I remembered that Newton had to build the differential calculus to formulate his mechanics. Consequently, I reinspected the differential calculus (still essentially the same since Newton's time), to see whether it was indeed applicable to hadronic mechanics and discovered that it was not because, contrary to popular beliefs in mathematics and physics for about four centuries, a conventional. differential, such as that of the coordinate dr, is indeed dependent on the basic unit I of the field when the latter has a functional dependence on the local variable, I* = I*(r, ...) = 1/T(r, ...). In fact, in this case the coordinate has to be an isocoordinate, r* = r I*, as a result of which d*r* ≠ dr. In this way, I formulated the isodifferential calculus for which
I published this discovery in 1996 at the Rendiconti Circolo Matematico Palermo,
Nonlocal-integral isotopies of differential calculus,
mechanics and geometries
R. M. Santilli, Rendiconti Circolo Matematico Palermo, Suppl. Vol. 42, 7-82 (1996).
The new differential calculus finally allowed me to reach a consistent formulation of the linear momentum with isotopic and genotopic expressions fully compatible with the corresponding Lie-isotopic and Lie-admissible liftings of Heisenberg and Schroedinger equations
where I*r = 1/Tr, I*t = 1/Tt are the space and time isotopic units and elements, respectively, with corresponding expressions for the genotopic lifting. It was then easy to prove the desired invariance over time of hadronic mechanics, including the preservation of the basic unit, Hermiticity-observability, and all numerical predictions under the same conditions at subsequent time.
Following these resolutions, I separated myself from the rest of world for one entire year thanks to help from my wife Carla for food and support (without my wife's help hadronic mechanics would never have seen the light), and I wrote the second edition of "Elements of Hadronic Mechanics," Volumes I and II that I released for publication by the Ukraine Academy of Science in 1995.
Following submission in 1995, all the background mathematics was published in 1996 by the Rendiconti Circolo Matematico Palermo. I reached the crucial invariance over time for the case of isomechanics in the 1997 paper
Relativistic hadronic mechanics: nonunitary, axiom-preserving
completion of relativistic quantum mechanics
R. M. Santilli,
Found. Phys. Vol. 27, 625-729 (1997)
I then reached the invariancve over time for the much more complex Lie-admissible irreversible mechanics in the subsequent paper also of 1997 that completed the formal construction of hadronic mechanics
Invariant Lie-admissible formulation of quantum deformations
R. M. Santilli,
Found. Phys. Vol. 27, 1159- 1177 (1997)
After that time, studies on the various applications and experimental verifications of hadronic mechanics increased exponentially thanks to the contribution by numerous colleagues. As indicated in my papers, colleagues who do not care to participate in basic new advances essentially make a gift of scientific priorities to others.
Main references of hadronic mechanics
The main references on hadronic mechanics are the following: the analytic foundations were treated in the two monographs of 1978 and 1982 hereon referred to as FTP Volumes I and II
"Foundations of Theoretical Mechanics, I: The Inverse Problem in Newtonian Mechanics"
R. M. Santilli, Springer-Verlag (1978)
"Foundations of Theoretical Mechanics, II: Birkhoffian Generalization of hamiltonian Mechanics"
R. M. Santilli, Springer-Verlag (1982);
The first comprehensive axiomatically consistent treatment of hadronic mechanics can be found in the two monographs hereon referred to for brevity 1995 EHM Volumes I and II
"Elements of Hadronic Mechanics", Vol. I: "Mathematical Foundations"
R. M. Santilli, Ukraine Academy of Sciences (1995),
"Elements of Hadronic Mechanics"
Vol. II: "Theoretical Foundations"
R. M. Santilli, Ukraine Academy of Sciences (1995)
A recent Lie-admissible formulation of hadronic mechanics can be found in the memoir published by the Italian Physical Society
Lie-admissible invariant representation of irreversibility for matter and antimatter at the classical and operator level
Ruggero Maria Santilli
Nuovo Cimento B Vol. 121, p. 443-595 (2006)
and the most recent presentation is available in the five volumes hereon referred to as 2008 HMMC Volumes I, II, III, IV, V
Hadronic Mathematics, Mechanics and Chemistry, Volumes I, II, III, IV and V:
R. M. Santilli, International Academic Press (2008)
Iso-, geno-, hyper-mechanics for matter, their isoduals for antimatter, and their novel applications to physics, chemistry and biology
R. M. Santilli,
Journal of Dynamical Systems and Geometric Theories, Vol. 2, pages 121-194 (2003)
"Santilli's Lie-Isotopic Generalization of Galilei and Einstein Relativities"
A. K. Aringazin, A. Jannussis, F. Lopez, M. Nishioka and B. Veljanosky,
Kostakaris Publishers, Athens, Greece (1991)
"Santilli's Isotopies of Contemporary Algebras
Geometries and Relativities"
J. V. Kadeisvili,
Ukraine Academy of Sciences
Second edition (1997)
"Mathematical Foundation of the Lie-Santilli Theory"
D. S. Sourlas and G. T. Tsagas,
Ukraine Academy of Sciences (1993)
Prizes and nominations
Santilli has received large financial rewards from the new industrial applications of hadronic mechanics in physics, chemistry and biology. He has been listed by the Estonia Academy of Sciences among the most illustrious applied mathematicians of all times because of his discovery of the Lie-admissible covering of all of 20th century mathematics that encompasses all possible mathematics with an algebra (Chapter 2) and, consequently, all possible physical and chemic;l theories with an algebra in the brackets of their time evolution (Chapters 3-9), the listing of Santilli name being done with the quotation his 1967 initiation paper on Lie-admissible algebras jointly with the names of Gauss, Hamilton, Lie, Jordan, Wigner, and others very famous mathematicians (the only name of Italian origin appearing in the list). A motivation has been that
.... several other mathematicians have discovered individual mathematical structures, for instance, Hamilton discovered the quaternions, Jordan discovered his algebras, and Lie discovered his theory, but no other mathematician in history discovered, as Prof. Santilli did, structural generalizations of the totality of mathematics in sequential series [isotopic, genotopic, hyperstructural and isodual].
Additionally, a lecture room at a research center in Australia has been called "Santilli Hall."Besides various gold medals for scientific merits, Santilli has received in January 2009 the prestigious prize of the Mediterranean Foundation, previously granted to Price Albert of Monaco , France President Nicolas Sarkozy, Juan Carlos King of Spain, international architect Renzo Piano, and other famous people. Finally, Santilli has received hundreds of nominations for the Nobel prize in physiscs because of the construction of hadronic mechanics and more recently also for the Nobel prize in Chemistry. For details, one may visit the web site
Prof. Santilli's prizes and nominations
Acknowledgments
Jointly with the completion in 1997 of the formal construction of hadronic mechanics and its primary experimental verifications as well as applications in the 1997 paper
Relativistic hadronic mechanics: nonunitary, axiom-preserving
completion of relativistic quantum mechanics
R. M. Santilli,
Found. Phys. Vol. 27, 625-729 (1997)
Santilli released a rather vast acknowledgment to all institutions, journals and colleagues who helped the, or were exposed to the construction of hadronic mechanics. The Foundation has retrieved the preprint and provides below the original version of the Acknowledgments since they had to be reduced in the published version by editorial request.
1996 SANTILLI ACKNOWLEDGMENTS
It is a pleasant duty to express my sincere appreciation to th referees of Foundations of Physics for a very accurate control of the manuscript and for simply invaluable critical suggestions.
It is also a duty to express my appreciation to a number of institutions, journals and colleagues for hospitality and invaluable help during the laborious studies in the construction of hadronic mechanics and its verification conducted during the past three decades.
First, I would like to thank the following Institutions:
The University of Naples, Italy, where I conducted my undergraduate studies in physics for an unforgettable human and scientific experience. I want to remember and thank in particular my mathematics teacher Renato Caccioppoli for propagating to be his passion for mathematics that set the direction of the rest of my scientific life.
The Department of Physics of the University of Torino, Italy, where I put the foundations of hadronic mechanics\ in the late 1960's as part of my Ph. D. thesis;
The Avogadro Institute in Torino, Italy, that gave me a chair in nuclear physics when quite young, with various students still remembering and tracing me down to this day;
The Center for Theoretical Physics of the University of Miami, Coral Gables, Florida, where I had a very enjoyable stay during the academic year 1967-1978;
The Department of Physics of Boston University where I taught, from prep courses to post Ph. D. Seminar courses in mathematics and physics from, 1968 to 19074;
The Center for Theoretical Physics of the Massachusetts Institute of Technology, where most background technical preparation was conducted in the mid 1970's, such as the papers on the existence and construction of a Lagrangian in field theory, the paper on the identification of gravitational and electromagnetic interactions, the preliminary versions of monographs published by Springer Verlag, and other studies;
The Department of Mathematics of Harvard University, were the main papers proposing the construction of hadronic mechanics and numerous other works were written in the late 1970's and early 1980's under support from the U. S. Department of Energy;
The Joint Institute for Nuclear Research, Dubna, Russia, for summer hospitality in recent years, where several papers were written, such as the crucial paper on isonumbers, genonumbers and their isoduals, the paper on the synthesis of the neutron first appeared as JINR Communication Number E4-93-352, and other papers,
The Institute for High Energy Physics, Protvino-Sherpukov, Russia, also for summer hospitality in recent years, where the most innovative studies in gravitation were initiated,
The International Center for Theoretical Physics in Trieste, Italy, for a short visit in 1992;
CERN, Geneva, Switzerland, also for a short stay in 1992;
The Institute for Basic Research on Harvard Grounds from 1982 to 1989 and then in Palm Harbor Florida from 1989 to present where the main research on hadronic mechanics has been conducted and continued to this day;
and numerous other Institutions for shorter stays.
I would like to express my appreciation for recent hospitality I received for presentations on various aspects of hadronic mechansics at the following meetings (up to 1996):
Three Workshops on Lie-admissible Formulation, Harvard University, 1978-1981;
International Conference on nonpotential interactions and their Lie-admissible treatment, University of orleans, France, 1982;
Nine Workshops on Hadronic mechanics from 1981 to present held at various institutions in the Boston, Area (USA), Belgrad (Yugoslavia), Patras (Greece), Como (Italy), London (England), Beijing (China), and other locations;
International Workshop on Symmetry Methods in Physics, J.I.N.R., Dubna, Russia, July 1993;
Third International Wigner Symposium, Oxford University, Oxford, England,September 1993;
International Conference
XVI-th [1993], XVII-th (1994) and XIX-th (1996) International Workshop on High Energy Physics and Field Theory, I. H. E. P., Protvino-Sherpukov, Russia, September 1993;
International Conference on the Frontiers of Fundamental Physics, Olympia, Greece, September 1993;
VI-th Seminar on High Temperature Superconductivity, J.I.N.R., Dubna, Russia, September 1993;
Seventh Marcel Grossmann Meeting on General Relativity and Cosmology, Stanford University, Stanford, CA, U.S.A., July 1994;
1996 Sanibel Symposium, St. Augustine, Florida, March 1995 and February 1996;
First Meeting for the Saudi Association for Mathematical Sciences, Riyadh, Saudi Arabia, May 1994;
International Conference on Selected Topics in Nuclear Structure, J.I.N.R., Dubna, Russia, July 1994;
International Workshop on Differential Geometry and Lie Algebras, Thessaloniki, Greece, December 1994;
HyMag Symposium, National High Magnetic Field Laboratory, Tallahassee, Florida, December 1995;
International Workshop on new Frontiers in Gravitation, Istituto per la Ricerca di Base, Castle Prince Pignatelli, Monteroduni, Italy, August 1995;
National Conference on Geometry and Topology, Iasi, Rumania, September 1995
International Symposium for New Energy, Boulder Colorado, April 1996;
International Workshop on the Gravity of Antimatter and Anti-Hydrogen Atom Spectroscopy, Sepino, Italy, May, 1996;
Workshop on Differential geometry, Palermo, Italy, June 1996;
International Workshop on Polarized Neutrons, J.I.N.R., Dubna, Russia, June 1996.
Special thanks are also due for the recent opportunity of delivering lectures or short seminar courses on the various aspects of hadronic mechanics at:
Moscow State University,Moscow, Russia, August 1993;
Estonia Academy of Sciences, Tartu, August 1993;
Theoretical Division, J.I.N.R., Dubna, Russia, September 1993; August 1994; August 1995; August 1996;
Ukraine Academy of Sciences,Kiev, September 1993;
Institute for Nuclear Physics, Alma Ata, Kazakhstan, October 1993;
Institute for High Energy Physics, Protvino, Russia, June 1993, June 1994, June 1995;
Theoretical Division, C.E.R.N, Geneva Switzerland, December 1994;
Department of Mathematics, Aristotle University, Thessaloniki, Greece;
Department of Mathematics, King Saud University, Riyadh, Saudi Arabia;
Demokritus Institute, Athens, Greece, December 1994;
Institute of Nuclear Physics. Democritos University of Thrace Xanthi, Greece, December 1994;
Institute for Theoretical Physics, Wien, Austria, December 1994;
Department of Mathematics, University of Constanta,Romania, September 1995;
Research Center COMSERC, Howard University, Washington, D.C., U.S.A. April, 1995;
Department if Mathematics, Howard University, Washington, D. C., U.S.A., April 1995;
The International Center for Theoretical Physics (ICTP), Trieste, Italy, 1992;
Department of Nuclear Physics, University of Messina, Italy, June 1996;
Department of Mathematics, University of Palermo, Italy, June 1996;
Academia Sinica, Beijing, China, supper 1995;
The Italian national Laboratories in Frascati, Italy, 1977;
The Center for Theoretical Physics of the Massachusetts Institute of Technology, 1976
The Lyman Laboratory of Physics, Cambridge, MA, 1978, delivering a seminar course on the integrability conditions for the existence of a Lagrangian in Newtonian mechanics and field theory;
The University of illinois in bloomington, 1968;
Russia Academy of Sciences,Moscow, June 1996;
and other institutions in various countries. I have no word to express my sincere appreciation and gratitude to all colleagues at the above meetings or institutions for invaluable critical comments.
Additional thanks for the critical reading of parts of this paper are due to: M. Anastasiei, Yu. Arestov, A. K. Aringazin, A. K. T. Assis, M. Barone, Yu. Barishev, J. Ellis, T. Gill, J. V. Kadeisvili, A. U. Klimyk, A. Jannussis, N. Makhaldiani, R. Miron, M. Mijatovic, D. Rapoport-Campodonico, D. Schuch, G. T. Tsagas, N. Tsagas, C. Udriste, T. Vougiouklis, H. E. Wilhelm, and others.
Finally, this paper has been made possible by rather crucial publications appeared in the following Journals, here acknowledge with sincere appreciation:
Foundations of Physics, for publishing: this memoir, the first after the achievement of axiomatic maturity in relativistic hadronic mechanics; the 1981 article on the apparent impossibility for quarks to be elementary at a time of widespread belief to the contrary; and several related articles in classical and operators studies not quoted for brevity;
Physical Review A, for publishing the important article by Schuch on the need for nonunitary treatment of nonlinear operator systems;
Physical Review D, for publishing the 1981 article on the need to verify the validity of Pauli's principle under nonconservative conditions due to external strong interactions;the 1978 article {3c} on the isotopies of electroweak interactions with a breaking of the gauge invariance; and other papers;
Hyperfine Interactions, for publishing the paper on the prediction of a novel light emitted by antimatter;
Nuovo Cimento, for the publication of: the 1967 article on the first Lie-admissibity in the physical literature; the 1983 article on the first isotopies of Minkowski spaces, the Lorentz symmetry and the special relativity the 1983 article {4f} on the first operator realization of isosymmetries via a lifting of Wigners theorem; the 1982 article on the first Lie-admissible time-irreversible formulation of open strong interactions; the article on the first isotopies of SU(3), article, the scattering theory, and several other seminal papers;
The (MIT) Annals of Physics, for the publication of the 1976 articles on the integrability conditions for the existence and computation of a Lagrangian in field theory, the 1982 article on the crucial identification of the gravitational and electromagnetic fields from the primary electromagnetic origin of mass (that subsequently rendered unavoidable the prediction of antigravity), and others;
Journal of Physics G, for publishing the 1981 articles on the rather crucial isominkowskian representation of the behavior of the meanlives of K-o with energy, and other papers;
Physica, for publishing the 1985 article on the possibility of regaining convergent perturbative series for strong interactions, and others;
Physics Essays, for publishing the 1992 article on classical realizations of Santilli's isogalilean relativity, and the article on the representation of the difference between cosmological redshifts of physically connected quasars and galaxies via Santilli's isospecial relativity, and others;
Communications in Theoretical Physics, for publishing a number of crucial articles, such as the first article on the isotopic quantization of gravity, the first article on the isoquark theory, the first article on the isodual representation of antimatter, the first article on the paradox of quantum mechanics at the limit of gravitational singularities, and several others;
Annales de la Fondation Louis de Broglie, for publishing the crucial articles on the limitations of current generalized theories, and others;
Revista Tecnica, for the publication of articles on the isotopies of Newtonian, analytic and quantum mechanics;
Journal of Moscow Physical Society, for the publication of the comprehensive 1993 article on the isotopies and isodualities of the Poincare~ symmetry, including the universal symmetry of all possible Riemannian and Finslerian line elements, which is the single most important paper of these studies from which all results can be uniquely derived;
J.I.N.R. Rapid Communications for the publication of the crucial 1993 article on the isotopies of SU(2)- spin with the isopauli's matrices and the reconstruction of the exact isospin symmetry in nuclear physics;
International Journal of Quantum Chemistry, for the publication of the crucial 1981 article on the application and experimental verification of hadronic mechanics to superconductivity, with the first attractive force among two identical electrons in singlet couplings at mutual distances smaller than their coherent length;
Chinese Journal of Systems Engineering and Electronics, for the publication of the crucial 1995 article on the isotopies of the spinorial covering of the Poincare~ symmetry and of Diracs equations, with application to the synthesis of the neutron from protons and electrons only, and other articles;
Mathematical Methods in Applied Sciences, for the publication of the recent comprehensive study {5g} by Kadeisvili on the Lie-Santilli isotheory and related methods;
Rendiconti Circolo Matematico di Palermo for the publication of an entire 1996 issue of of their Supplemento entirely dedicated to the new mathematics underlying hadronic mechanics;
Acta Applicxandae Mathematica for the publication in 1995 of th crucial application of hadronic mechanics to Bell's inequality, the isotopies of the SU(2) spin symmetry and all that;
The Indian mathematical Society, for the publication of numerous seminal papers in pure and applied mathematics at the foundation of hadronic mechanics.
Particular thanks are additionally due to all past and present Editors of the Hadronic Journal and Algebras, Groups and Geometries for their continued encouragement, support and control of various publications quoted in this paper.
Additional thanks are due to the participants, editors and and publishers of the Proceedings of some eighteen international workshops and conferences held in the field of hadronic mechanics in the USA, Europe, and China resulted in a total of over thirty volumes, which are too numerous to mention here individually.
I must also express my utmost gratitude to G. F. Weiss, S. Smith and P. Fleming, staff of our Institute for basic Research in Palm Harbor, Florida, and numerous other members and visitors through the years, for simply invaluable help, assistance and control in the preparation of this manuscript.
It is also my pleasant duty to thank several colleagues for their invaluable contributions in the construction of the hadronic mechanics, particularly during the early years of its study, including: S. Okubo, H. C. Myung, R. Mignani, F. cardone, A. K. Aringazin, A. Kalnay, A. O. E. Animalu, D. Schuch, T. L. Gill, Gr. Tsagas, D. S. Sourlas, J. V. Kadeisvili, E. B. Lin, M. Nishioka, A. Jannussis, G. Eder, J. Fronteau, M. Gasperini, D. Brodimas, P. Caldirola, M. Mijatovic, Y. Prigogine, K. Popper, B. Veljanoski, A. Tellez-Arenas, and others.
I cannot close these Acknowledgments without expressing my appreciation to the American, British, Italian, Swedish, French, German, Russian, Chinese physical and other societies for their role in the construction of hadronic mechanics, On my side, I would lille to indicate that. when facing truly fundamental structural advances of pre-existing knowledge as it is the case here, the "burden of proof" on their validity belongs to the author(s) and definitely not to the societies, since their historical as role is that of exercising caution for the very protection of science. On the other side, scientific societies are suggested to exercise tolerance when attacked for insufficient scientific democracy at the time when the battle for new scientific vistas reaches its climax.
I cannot close these Acknowledgments without expressing my deepest appreciation to the United States of America for being so generous to me and my family, by permitting me to realize my scientific dreams on hadronic mechanics as well as my personal dreams in the American way of life, sports cars and boats, generosity that has caused in me an unbounded allegiance.
It is a truism to say that. without my conduction of research in the U.S.A., hadronic mechanics would not have been completed and established because, even though its main lines had been conceived in Italy, the realization of the above indicated "burden of proof" required "experiumental verifications and novel industrial applications relevant to society" that would have been of difficult realization elsewhere because they must be achieved nowadays outside academia whenever dealing with basic advances over pre-established doctrines, as well known to insiders.
On my part, I considered myself a "special immigrant" because: I came here: from a rich Italian family, my father Ermanno Santilli being an Italian Medical Doctor and my grandfather Ruggero Santilli being an Italian industrialist; after achieving in Europe the highest possible education in mathematics physics and chemistry; and while being the recipient of a chair in nuclear physics at the Avogadro Institute in Torino.
The construction and proof of hadronic mechanics were possible "by" (rather than "in") the U.S.A. amidst incredible, well known and documented academic obstructions (at time reaching true levels of hysteria against the surpassing of beloved old doctrines), because of: the inspired values of the U. S. Constitution, the best throughout history I ever read; the crucial democracy of its Institutions; and its unique multitude of overlapping social, governmental and industrial structures offering people a variety of ways to realize their dreams, but only following fierce determination, relentless commitment and true values.
Most special thanks are finally due to my wife Carla for her grace, class, patience and support in enduring predictable obstructions in the conception, completion and proof of hadronic mechanics.
Needless to say, I am solely responsible for the content of this paper owing to the numerous changes occurred during the preparation of the final version.
3.11C. Interior and exterior dynamical systems
As santilli recalls, physical systems were classified by Lagrange, Hamilton, Jacobi and other founders of mechanics into:
1) Exterior dynamical systems, consisting of a finite number of point-like particles moving in vacuum (conceived as empty space) without collisions. Note that the lack of collisions is sufficient to admit an effective point-like approximation of particles and, vice versa, the assumption of a point-like structure implies the tacit assumption of lack of collisions since dimensionless points cannot collide. Typical classical examples are given by the Solar system or a spaceship in orbit around Earth in vacuum since in both cases the actual size and shape of the constituents (the planets or the spaceship) do not affect the dynamical evolution, and said constituents can be well approximated as massive points. Typical particle counterparts are given by the atomic structure, particles in accelerators, crystals and other systems admitting a good approximation of the constituents as being dimensionless. Note also that all exterior systems are purely Lagrangian or Hamiltonian, in the sense that the knowledge of only one quantity, a Lagrangian or a Hamiltonian, is sufficient to characterize the entire dynamics.
2) Interior dynamical systems, consisting of a finite number of constituents moving within a physical medium, in which case point-like abstraction are no longer valid, since the actual size and shape of the constituents has direct implications in the dynamical evolution. Typical classical examples are given by the structure of a planet such as Jupiter or a spaceship during re-entry in our atmosphere. Typical particle examples are given by the structure of the Sun or, along similar lines, the structure of nuclei and hadrons since, in all these cases, motion of one constituent occurs within the medium characterized by the wavepacket of other surrounding constituents. Note that interior systems are non-Lagrangian and non-Hamiltonian, in the sense that a given Lagrangian or Hamiltonian is insufficient to characterize the dynamics due to the need for a second quantity characterizing the contact interactions represented with external terms in the analytic equations (1.2).
As reviewed in Section 3.9, the above classification was eliminated in the 20th century by organized interests on Einsteinian doctrines via the abstraction of all particles as being point-like, consequential elimination of the contact non-Lagrangian or non-Hamiltonian interactions, and consequential elimination of interior dynamical systems.
As indicated in Section 1.1, the first and perhaps most fundamental scientific contribution by Santilli has been to prove via Theorem 1.1 that the above abstraction was a figment of academic imagination. In any case, the inconsistency of most of the 20th century particle physics can be unmasked by noting that both elastic and inelastic scattering events are impossible for dimensionless particles by conception, again, because dimensionless particles cannot influence the trajectories of other dimensionless particles except for Coulomb interactions. Alternatively, the experimental evidence of deflection of trajectories in scattering processes from a purely Coulomb behavior is evidence on the existence of non-Lagrangian and non-Hamiltonian interactions precisely according to Theorem 1.1.
It is evident that Santilli's studies, including those on hadronic mechanics, specifically refer to interior dynamical systems that will be the sole system considered hereon. As we shall see, the second quantity needed for the representation of size, shape and dynamics of interior systems will be given by the isounit. Hence, special relativity and quantum mechanics are hereon assumed as being exactly valid for exterior dynamical systems, and Santilli's isorelativity and hadronic mechanics are hereon assumed as being exactly valid for interior dynamical systems with unique and unambiguous interconnecting limits characterized by the isounit alone.
For references in the above classification, including an accurate historical analysis, we refer the serious scholar to the 1995 FTM Volumes I and II. An instructive reading in the topic of this section is also that of Santilli's ICTP paper
Inequivalence of exterior and interior dynamical problems
3.11D. Closed and open dynamical systems
Lagrange, Hamilton, Jacobi and other founders of mechanics introduced the following additional classification of dynamical systems:
A) Closed dynamical systems, given by systems that can be well approximated as being isolated from the rest of the universe, thus verifying the ten conservation laws of total quantities characterized by the Galilei or the Poincare' symmetry (the conservation of the total energy, linear momentum, angular momentum and the uniform motion of the center of mass). This is typically the case for both exterior and interior systems, whether at the classical or operator levels, when isolated from the rest of the universe.
B) Open dynamical systems, given by system in interaction with an external component under which at least one of the ten Galilei's or Poincare' conservation laws is not verified due to exchanges of physical quantities between the system considered and the external component. Needless to say, when the external component is included, the open system is completed into a closed form.
Again, for the intent to adapt nature to Einsteinian and quantum theories, another widespread belief of the 20th century physics has been that "closed systems can solely admit conservative-potential forces" or, equivalently, that internal, contact, nonpotential interactions do not verify all ten Galilean or Poincare' conservation laws and, consequently, the contact-nonpotential forces "do not exist in particle physics".
The above belief has caused an alteration of physical research of historical proportions because the belief is at the foundation of some of the most equivocal assumptions of the 20th century physics, such as the belief that Einstein's special relativity and quantum mechanics are exactly valid for the structure of hadrons, nuclei and stars. The political argument (political because without a serious scientific basis) is that said systems verify the ten total conservation laws when isolated from the rest of the universe. Hence, the argument says, Einsteinian doctrines and quantum mechanics hold for their interior.
Santilli has disproved this additional academic belief with his notions of:
I) Closed non-Hamiltonian system, or, more technically, closed variationally nonselfadjoint systems (see Section 2.9), given by systems verifying the ten Galilean or Poincare's conservation laws, thus being closed, yet they admit internal forces that are Hamiltonian as well as non-Hamiltonian or, more technically, variationally selfadjoint (SA) and nonselfadjoint (NSA).
II) Open non-Hamiltonian systems, or open variationally nonselfadjoint systems, given by systems that do not verify at least some of the ten Galilean or Poincare' conservation laws due to non-Hamiltonian, or nonselfadjoint interactions with an external system. It is evident that these systems are irreversible over time.
In fact, Santilli proved in the 1982 FTM Volume II, page 235, that a Newtonian system of two or more particles with potential/selfadjoint and nonpotential/nonselfadjoint forces
The operator counterpart of closed non-hamiltonian system is easily provided by Santilli's Lie-isotopic theory (Section 2.7), in general, and the Galilei-Santilli or Lorentz-Poincare'-Santilli isosymmetry, because: the ten conventional generators, representing the ten total conserved quantities are preserved identically by the isotopic symmetries; the selfadjoint forces are represented by the Hamiltonian; and the nonpotential forces are represented by the isounit I*(t, r, p, ...) = 1/T(t, r, p, ...), as we shall see. The totally symmetric character of the Lie-isotopic product [Q, H]* = QTH - HTQ assures total conservation laws.
Nevertheless, closed non-Hamiltonian systems admit internal exchanges of all physical quantities, that is, we have internal exchanges not only of the energy, but also of mass, charge, angular momentum, spin, etc. without any conflict with total conservation laws since we merely have internal exchanges that compensate each other in their sum due to the isolated character of the system. As we shall see in the next chapters, this feature alone of hadronic mechanics has far reaching implications and applications mostly beyond our imagination at this writing.
The case of open non-Hamiltonian systems is the second fundamental class of systems studied by hadronic mechanics and includes all energy releasing processes. These systems require Santilli's Lie-admissible theory (Section 2.8), since the lack of totally antisymmetric character of the brackets (Q, H)* = QRH - HSQ in the time evolution law (3.110) assures the description of time rate of variations of physical quantities of which conventional conservation laws are a particular case, in the same way as Santilli isoalgebras are a particular case of Santilli's Lie-admissible algebras.
The classical notion of closed non-Hamiltonian systems was introduced in the 1982 FTM Volume II, with the operator counterpart presented in various papers (see EHM and HMMC). An instructive reading is also that of the ICTO paper
Closed systems with non-Hamiltonian internal forces
3.11E. Newton-Santilli isoequations
>From Theorem 1.1, the central problem addressed by Santilli was the achievement of a mathematically and physically consistent, classical and operator formulation of non-Hamiltonian (or variationally nonselfadjoint) forces, whose correct quantization had escaped all attempts during the 20th century. Santilli knew that such an objective cannot be achieved without an action principle, since the latter is crucial for a consistent map from classical to operator forms.
But, Newtonian systems with nonpotential forces FNSA(t, r, v, ...) do not admit any action principle (when formulated with conventional mathematics). Thus, Santilli searched for an identical reformulation of Newton's equation (3.127) capable of admitting a covering action principle suitable for consistent maps to operator forms. It is at this point where the dimension of Santilli's scientific edifice can be appraised, since it encompasses a variety of discoveries in various branches of mathematics, physics and chemistry, all part of one single monolithic structure that will indeed resist the test of time due to its axiomatic consistency, beauty, experimental verification and industrial applications.
Santilli struggled for decades to reformulate Newton's equations into a form admitting a covering variational principle without success, until he discovered the iso-, geno- and hyper-differential calculus in the mid 1995, that allowed him to achieved a series of structural generalization of Newton equations since Newton's "Principia" of 1687, the first known to the Foundation (evidence of dissident views is solicited for presentation in this section). The broader equations are today known as Newton-Santilli iso-, geno-, hyper- and isodual equations. Regrettably, we can solely indicate here the Newton-Santilli isoequations and refer the scholar to the literature available in free download.
Let Stot(t, r, p) = E(t, x, It) x E(r, x, Ir) x E(v, x, Iv) be the Kronecker product of the representation spaces for the Newton equations with time t, coordinates r and velocity v, conventional associative multiplication axb = ab, and units It = 1, Ir = Ip = Diag. (1, 1, 1). Santilli introduces the following isotopies of the Newtonian representation space with related isocoordinates, isoproducts and isounits (Section 2)
To understand the advance over Newton's original conception, the serious scholar should note that the conventional Newton equations can only represent point-like particles due to the background local-differential topology and geometry, while the Santilli's covering equations represent particles with their actual extended shape under the most general possible potential and nonpotential interactions, due to the background novel isotopology.
Additionally, Santilli has provided the genotopic, hyperstructural and isodual coverings of Newton's equations for irreversible and multivalued matter systems and antimatter systems, respectively, that we cannot possibly review here.
Hence, to select the appropriate covering of Newtonian mechanics, one should identify whether the considered classical equations deal with: A) matter or antimatter; B) Closed or open systems; and C) Single-valued or multi-valued systems. Then, one should select the appropriate covering mechanics. Mathematically inclined scholars should know that Santilli has provided one single abstract formulation encompassing all possible eight different equations, including the conventional, iso-, geno-, hyper-systems and their isoduals, although such a unified treatment is not recommended for physical applications because excessively abstract.
Santilli's coverings of Newton's equations and mechanics can be studied in the 1996 RCMP memoir, and in EHM Volumes I and II.
3.11F. Hamilton-Santilli isomechanics
The embedding of the external terms in Lagrange's and Hamilton's equations in the generalized units, and the consequential regaining of a variationally selfadjoint formulation on isospaces over isofields, have far reaching implications. To begin, the true Hamilton's equations (1.2) are identically rewritten in the form known as Hamilton-Santilli isoequations,
Recall that Hamilton's equations with external terms do not characterize any algebra with the brackets of the time evolution, let alone violate all Lie algebras (Section 1.1). Via Eqs.(3.139), Santilli restores an algebra in the brackets of the time evolution with external terms, and this algebra results to be a Lie isoalgebra as a covering of the algebra for the truncated analytic equations. In fact, Eqs. (3.139) characterize the time evolution of a physical quantity Q(t)
Among an infinite number of algebraic solutions, a simple one is given by
The Hamilton-Jacobi-Santilli isoequations on isospaces over isofields expressed in terms of isocoordinates are given by
Note from Section 3.11D that the Hamilton-Santilli isomechanics is solely applicable to closed non-Hamiltonian systems, trivially, because the antisymmetric character of the brackets of the time evolution imply the conservation of the Hamiltonian and other physical quantities.
Again, to select the appropriate covering mechanics, one should identify whether the considered system deals with: A) matter or antimatter; B) Closed or open systems; C) Single-valued or multi-valued systems. The selection of the appropriate mechanics is then consequential.
The topic of this section can be best studied in the 1996 RCMP memoir, or in EHM Volumes I and II.
3.11G. Animalu-Santilli isoquantization
The conventional naive quantization maps the Hamiltonian action into an expression depending on Planck's constant
The map of the Hamilton-Santilli isoaction into an operator form was first identified by A. O. E. Animalu and R. M. Santilli at the XII Workshop on Hadronic Mechanics of 1990, it is today called the Animalu-Santilli isoquantization, and can be written
Consequently, map (3.150) represents the fundamental assumption of hadronic mechanics according to which Planck's constant becomes a locally varying operator representing the impossibility to have quantized orbits for an extended particle immersed within a hyperdense medium as it is the case, for instance, for an electron in the core of a star, under the condition (3.151) of recovering conventionally quantized orbits when motion returns to be in vacuum.
Hence, the serious scholar accustomed to the usually quantized orbits for the structure of atoms should not expect the same quantized orbits in the interior of hadrons, nuclei or in the core of stars to avoid evident contradictions. More specifically, when a hadronic constituent is subjected to an excited orbit, that orbit is expected to be in vacuum, rather than in the interior of hadrons, thus belonging to quantum rather than hadronic mechanics. As we shall see in Section 4, this aspect is very insidious and confuses the problem of classification of hadrons generally searched via a spectrum of quantum states, with the structure of one individual hadron for which only one orbit is possible at mutual distances smaller than the size of the wavepackets of particles.
For references and a detailed presentation, the serious scholar is suggested to study EHM Volume II and HMMC Volume III. The original contribution by Animalu and Santilli is available from the pdf file
title to be added
3.11H. Hilbert-Santilli isospaces
The isotopic branch of hadronic mechanics is formulated on Hilbert-Santilli isospaces Η* that are the image of conventional Hilbert spaces Η over a conventional field F under nonunitary transformations (see Section 3.xx below), with isostates |ψ*), isoinner product defined on an isofield F*
A fundamental property is that, if an operator Q is Hermitean on Η over F, then it is iso-Hermitean, namely, it verifies the condition of Hermiticity on Η* over F*,
Note that I* is indeed the correct right and left unit of the isotopic branch of hadronic mechanics because it verifies the identities
3.11I. Schroedinger-Santilli isoequations
As indicated earlier, the first lifting of Schroedinger's equations was done by Santilli in 1979, and reinspected in various works. The final version was reached by Santilli in the 1996 RCMP memoir as part of the discovery of the differential calculus. The desired equations can be expressed via the image of the Hamilton-Jacobi-Santilli isoequations (3.145)-(3.147) under map (3.149). For the simple case of a constant isounit, or an isounit averaged to constant, the isoequation can be written
Via elementary calculations, the above equations can be written in the final form known as Schroedinger-Santilli isoequations
The study of open irreversible single or multi valued matter systems and their antimatter counterparts requires the use of Schroedinger-Santilli geno-, hyper- and isodual equations, respectively, we cannot possibly review here.
Serious scholars are suggested to study EHM Volumes I and II and HMMC Volume III.
3.11J. Heisenberg-Santilli isoequations
The isotopies of Heisenberg's equations were discovered by Santilli in the 1978 original memoirs, their final version was also reached in the 1996 RCMP memoir jointly with the discovery of the isodifferential calculus, are today called Heisenberg-Santilli isoequations, and can be written for the time evolution of an iso-Hermitean operator Q(t) in the finite form (with simplifications of inessential isoproducts and the simple assumption I*t = 1)
3.11K. Dirac-Myung-Santilli isodelta function and elimination of quantum divergencies
One of the main limitations of quantum mechanics has been the emergence of divergencies, such as the divergent character of the perturbation theory for strong interactions, divergencies in Feynman's diagrams, and others. One of the main contributions of hadronic mechanics is the elimination of quantum divergencies ab initio, thus permitting, for the first time in scientific history, convergent perturbative expansions for strong interactions.
As it is well known, the origin of the divergencies in quantum mechanics rests with the point-like abstraction of particles, which abstraction is technically represented by the Dirac delta function δ(r - ro) that is divergent at r = ro. However, the image of the Dirac delta function in hadronic mechanics, today known as Dirac-Myung-Santilli isodelta function from a paper of said originators of 1982, is given by
Additionally, for any given divergent or weekly convergent series Q(w) = I + w (Q H - H Q)/1! + ... → ∞, I = 1 there always exists an isounit I* = 1/T whose value (or average value) is much bigger than w (the isotopic element is much smaller than w) under which the above series becomes strongly convergent, namely, it verifies the expression where N is a finite positive number
Foundation of the hadronic generalization of atomic mechanics, II: modular-isotopic Hilbert space formulation of strong interactions
The name of Dirac-Myung-Santilli delta function was introduced by M. Nishioka in the following paper of 1984
Extension of the Dirac-Myung-Santilli delta function to field theory
See also by the same author
Realizations of hadronic mechanics
The above pioneering studies established the absence of quantum divergencies in hadronic mechanics and were followed by several studies reviewed in EHM Vol. II, including the convergence of isoperturbation expansions. The most recent contribution in the new scattering theory of hadronic mechanics (that will be reviewed in Chapter 5) is that of vthe paper.
Nonunitary-isoscattering theory, I: Basic formalism without difergencies for low energy reversible scattering
3.11L. Lie-admissible genotopic and hyperstructural branches of hadronic mechanics
The starting point for the geno- and hyper-coverings of isomechanics is, again, Newton's equation, this time for the embedding of irreversibility in the mathematical foundations of the dynamics, via the genotopic lifting of the basic unit of the Euclidean space and related associative product among two generic quantities Gk, k = 1, 2, into two inequivalent formulations, one to the right and a complementary one to the left (see Section 2.8), where, again, the symbols f and b denote forward and backward dynamics, respectively,
The next step is the selection of one direction in time, generally assumed to be the forward, and represent it with Santilli genomathematics to the right, that is, with genonumbers to the right, genospaces to the right, genogeometries to the right, etc. To avoid catastrophic inconsistencies often not noted by non-experts in the field, the above selection requires the religious restriction of all multiplication and other operations to the right.
Under the above foundations, we have the Newton-Santilli genoequations to the right
The hyperstructural branch to the right (primarily used for biological structures but also for multi-dimensional universes in physics) is essentially given by the above genotopic branch in which the genounits are assumed to be multi-valued, that is, to have a finite ordered set of values
A serious study of the above geno- and hyper-mechanics can only be achieved with a serious study of Santilli's 1996 RCMP memoir, the 1995 EHM Volumes I and II and the 2008 HMMC Volume III.
3.11M. Isodual branches of hadronic mechanics
Hadronic mechanics admits four different isodual branches for the representation of antimatter in conditions of increasing complexity according to the following classification:
1) isodual quantum mechanics, for the description of point-like abstractions of antiparticles in exterior dynamical conditions in vacuum (presented in Section 3.10);
2) Isodual isomechanics, for the description of closed non-Hamiltonian systems of extended antiparticles;
3) Isodual genomechanics, for the description of open systems of extended antiparticles; and
4) Isodual hypermechanics, for the description of multi-valued universes of antimatter..
All the above isodual mechanics can be constructed from the corresponding mechanics for matter via the application of the isodual map
For a serious knowledge we suggest again the study of Santilli's 1996 RCMP memoir, the 1995 EHM Volumes I and II and the 2008 HMMC Volume III.
3.11N. Two-body hadronic system
A typical two-body quantum mechanical system is given by the hydrogen atom in which the two constituents are well approximated as being point-like since the mutual distance is much bigger than the size of the wavepacket of the constituents. In this case, the system is entirely represented with a Hamiltonian of the type
Suppose that the two particles have the shape of spheroid ellipsoids with semiaxes nak2, a = 1, 2, k = 1, 2, 3. Clearly, the representation of these shapes is beyond any capability of a Hamiltonian, but shapes can be easily represented via Santilli's isounit.
Suppose that the above two extended particles with wavefunctions ψ1 and ψ2 are in conditions of partial mutual penetration (Figure 1.3), as it is the case for electrons in valence bonds, hadronic constituents, nuclear constituents and other structures. These physical conditions evidently cause nonlocal interactions extended over the volume of mutual overlapping that can be represented with volume integral ∫ ψ1†(r) ψ2(r) dr3.
Clearly, this mutual penetration cannot be represented with a quantum Hamiltonian for numerous reasons, beginning with a granting of potential energy to contact nonpotential effects, let alone the violation of the background local-differential topology. However, the same interactions can be readily represented with Santilli's isounit because the underlying topology is indeed nonlocal-integral.
By combining these and other aspects, we can see that the considered two-body hadronic system can be characterized by the Schroedinger-Santilli isoequation (3.162), or the Heisenberg-Santilli isoequation (3.166), with the same Hamiltonian H as in Eq. (3.182), plus the isotopic element T given by
where the exponent in general and the F function in particular, originate at the Newtonian level as in Eq. (3.138) and represent nonpotential interactions whose explicit form depends on the case at hand (see the applications in Chapters 4 and 5). Note that isotopic element (3.183) verifies the condition for strong isoconvergence of divergent quantum series, Eq. (3.169).
A most important feature of the above isotopic element is that, for mutual distances much bigger than 1 fm, the volume integral is null and the shapes become spherical due to absence of nonlocal interactions, thus verifying the basic condition (3.151), i.e.,
As a result, hadronic mechanics has been built to provide a "completion" of quantum mechanics solely applicable at short distances essentially along the historical argument by Einstein, Podolsky and Rosen (see below for more comments). As we shall see in the next chapters, two body hadronic bound states with Hamiltonian (3.182) and isotopic element (3.183), when applicable, provide exact numerical representations in various fields that are impossible with quantum mechanics.
3.11O. Simple construction of hadronic mechanics
It is important for readers to know that all mathematical and physical methods of hadronic mechanics can be constructed via the simple nonunitary transform of quantum models. This construction was first identified by Santilli in the 1978 original memoirs, studied extensively by various authors and will be heavily used in the subsequent outline of experimental verifications and applications of hadronic mechanics.
Construction of isomodels. The starting point is the identification of the nonunitary transform with the basic isounit of the model. For the case of two-body hadronic particles, the isounit is the inverse of the isotopic element (3.183), therefore yielding the identification
Once Santilli's isounit has been identified on groups of physical requirements (see the Chapters 4 and 5 for numerous realizations), the lifting of a quantum model into the hadronic form is simply achieved via the application of the above nonunitary transform to the totality of the mathematics and physics of the considered quantum model, without exceptions to avoid catastrophic inconsistencies.
In this way, we have: the very simple lifting of: the unit I of quantum mechanics into the isounit,
the lifting of Hilbert states | ψ ) into Hilbert-Santilli isostates | ψ* )
the lifting of the conventional Hilbert product into the inner isoproduct over the isofield of isocomplex isonumbers
the lifting of the conventional Schroedinger equation into the Schroedinger-Santilli isoequation
where one should note the change in the numerical value of the eigenvalue, E → E' called isorenormalization. In fact, E is the eigenvalue of H, while E' is the eigenvalue of the different operator HT, thus implying that E ≠ E'. Clearly, the isorenormalization of the energy is a fundamental feature of hadronic mechanics for numerous applications.
Construction of geno- and hyper-models. Genomodels are constructed via two different nonunitary transforms,
3.11P. Invariance of hadronic mechanics
As indicated earlier, the physical consistency of quantum mechanics is due to the invariance over time of: the basic units of measurements, the observability of operators and the preservation of the same numerical predictions under the same conditions at different times. Hadronic mechanics does indeed verify these central conditions of physical consistency, although at a covering level.
This feature can be simply seen as follows. Recall that the time evolution of hadronic mechanics is nonunitary when defined on a conventional Hilbert space defined over a conventional field of complex numbers. It is easy to see that, under these assumptions, hadronic mechanics is not invariant over time. In fact, following the identification of the isounit with a nonunitary transform, Eq. (3.186), a repeated application of the same transform does not leave invariant the isounit,
It is then easy to see that isounitary transformations preserve Santilli's isounit, thus preserving over time the basic units of measurements and the actual shape of particles,
It is also easy to prove that isounitary transforms preserve Hermiticity, thus preserving the observability of operators,
Finally, it is easy to see that isounitary transforms predict the same numerical values under the same conditions at different times because of the verification of the following condition at the isounitary level
The invariance of Lie-admissible branch of hadronic mechanics, when formulated on Hilbert-Santilli genospaces over genofields, follows the same lines. This invariance was first studied in the following 1997 paper
Invariant Lie-admissible formulation of quantum deformations
3.11Q. Relativistic hadronic mechanics
Foreword
Evidently, we cannot possibly review such a vast structure and are regrettably forces to provide the main lines solely for the isotopic branch, hereon referred to as isorelativistic hadronic mechanics.. The following paper presents relativistic isomechanics in a final invariant form
Relativistic hadronic mechanics: nonunitary, axiom-preserving
completion of relativistic quantum mechanics
The most comprehensive presentation of the field remains Santilli's 1995 monograph
"Elements of Hadronic Mechanics"
Vol. II: "Theoretical Foundations"
The primary scope of isorelativistic hadronic mechanics is to provide a quantitative representation of the mutations of "particles" into "isoparticles", namely, the alteration of the "intrinsic" as well as kinematic characteristics of particles in the transition from motion in empty space to motion within a hadronic medium, while recovering relativistic quantum mechanics uniquely and identically when the particles return to move in vacuum or, equivalently, when particles are at sufficient mutual distances to allow their point-like abstraction.
Recall that particles can be defiend as unitary irreducible representations of the Lorentz-Poincare' symmetry, while isoparticles can be defined as isounitary irreducble representations of the covering Lorentz-Poincare'-Santilli isosymmetry studied in Section 3.10 for the conventional case and in this section for the covering isospinorial form.
The mutation (also called isonormalization) of the rest energy of particles is an unavoidable consequence of all nontrivial isotopies of the Lorentz-Poincare' symmetry. However, the mutation of spin, charge and other intrinsic characteristics depends on the energy or, equivalently, the density of the hadronic medium considered.
This setting led Santilli to identify two main main cases, the first in which isoparticles maintain the conventional values of spin, charge and other characteristics, and the second in which these characteristic too are mutated.
We can now clarify the title of the memoir proposing the construction of hadronic ,mechanics,
Need of subjecting to an experimental verification the validity within a hadron of Einstein special relativity and Pauli exclusion principle
In essence, a particle with spin 1/2 preserves its spin under external electromagnetic interactions, as well known, in which case Pauli's principle is evidently verified. However, Santilli argued that particles may experience a mutation of their spin under external strong interactions, such as for nucleons passing very near nuclei considered as fixed and external, in which case an experimental verification of Pauli's principle and, consequentl,y of special relativity, is necessary.
The aspect that does not appear to have sufficiently propagated in the physics community, thus leading to misinterpretation or vacuous judgments, is that spin mutations are "internal" effects within hadronic matter that, as such, are not visible from the outside. Alternatively, Santilli argues that if a hadron has the conventional spin 1/2, this does not necessarily imply that its constituents have conventional spin because there could be internal mutations such to compensate each other resulting in the total spin 1/2, in a way similar to the mutual compensation of internal nonconservative forces resulting in total conservation laws (Section 3.11D). Hence, the :external" character of strong interactions is crucial to avoid vacuous claims of "experimental verification" of Pauli's exclusion principle.
Some 30 years following Santilli's call in 1978 to test Pauli's principle, a number of meetings have been recently organized in the subject (without consulting Santilli or quoting his 1978 origination). We assume the serious scholar is aware of the fact that any deviations from Pauli's principle is impossible when data are elaborated via quantum mechanics, since no spin mutation is the possible. Similarly, the serious scholar is assumed to know that hadronic mechanics is the only known axiomatically consistent mechanics predicting deviations from Pauli's principle under the indicated external strong interactions (the verification of Pauli's principle in heavy atoms causing deep wave overlappings of the wavepacksts of peripheral electrons with consequentioal nonlocalm nonunitary and nonquantum effects, can be done in a similar way by considering one peripheral electron while the rest of the system is assumed as external).>br>
Isolinearization of second order isoinvariants.
"Isotopic Generalization of Galilei and Einstein Relativities",
Volume I: "Mathematical Foundations"
"Isotopies of Galilei and Einstein Relativities"
Vol. II: "Classical Foundations"
Isorelativistic hadronic mechanics is then characterized by the Lorentz-Poincare'-Santilli isosymmetry of Section 3.10 defined on an iso-Minkowskian space M*(r*, m*, R*) under the interpretation of the generators as Hermitean operators on a Hilbert-Santilli isospace over the isofield R* with isounit I* = 1/T > 0 andrealization of the 4-dimensional isolinear (meaning linear on isospaces over isofields) momentum operator
The second order Casimir-Santilli isoinvariant (3.81) then yields the following Klein-Gordon-Santilli isorelativistic equation here written in its projection in our spacetime for simplicity
The "isolinearization" of the above second order isoequation has been studied extensively by Santilli, (see EHM Volume II) resulting in the Dirac-Santilli isoequation that we write in the simplified form also projected in our spacetime
Pauli-Santilli isomatrices
Isotopic lifting of SU(2)-symmetry with
application to nuclear physics,
Isorepresentation of the Lie-isotopic SU(2) algebra with application to nuclear physics and local realism,
and reviewed extensively in EHM-II Chapter 6. As indicated above, we have to distinguish the following two cases:
CASE I: Pauli-Santilli isomatrices without spin mutation
Let σk, k = 1, 2, 3, be the conventional Pauli matrices defined on a two-dimensional, complex valued, Euclidean space E(r, δ, R) with trivial metric δ = Diag. (1, 1, 1). Consider the Euclid-Santilli isospace E*(r*, δ*, R*) on a Hilbert-Santilli isospace with isostates |s*> and isometric
Prior to venturing vacuous judgments of triviality, serious readers should be aware that the above Pauli-Santilli isomatrices provide an explicit and concrete realization of hidden variables for
Isorepresentation of the Lie-isotopic SU(2) algebra with application to nuclear physics and local realism,
CASE II: Pauli-Santilli isomatrices with spin mutation
Among various cases identified by Santilli (see above quoted papers and EHM-II), an example of irregular Pauli-Santilli isomatrices is given by
Note that the irregular case can indeed be derived via a nonunitary transformation of the Lie case, but six dimensional (while that of the regular case was two dimensional, according to
By comparison, the Dirac-Santilli isoequation represents an isoelectron under "external" electromagnetic and contact nonpotential interactions, as necessary for the synthesis of the neutron from protons and electrons occurring in stars and studied in Chapter 7, since this case the wavepackets of the proton and electron are in conditions of mutual penetration, thus causing additional non-Hamiltonian interactions and related isorenormalizations.
Since the electron in vacuum has spin 1/2, the symmetry needed for the characterization of the isoelectron is given by the isotopy of the spinorial covering of the Lorentz-Poincare' symmetry, first studies by Santilli during his visit at the JINR in Dubna, Russia, Communication number E4-93-252 (1993), published in the 1995 paper
Recent theoretical and experimental evidence on the apparent
synthesis of neutrons from protons and electrons,
and today known as Santilli isospinorial covering of the Lorentz-Poincare' symmetry, that we write
By comparing isosymmetries (3.219) and (3.75), it is evident that SL*(2.c) is the isospinorial covering of SO*(3.1), T*(4) continues to represent isotranslations as in eqs. (3.88), and T*(1) continues to represent isotopic transforms as in Eq. (3.90).
Recall that, contrary to popular beliefs, Santilli has discovered a fundamental 11-th symmetry of the conventional Minkowskian spacetime used for grand unification, operator gravity and other important advances. Consequently, the Lorentz-Poincare' symmetry P(3.1), its isotopic covering P*(3.1) and its isospinorial covering Π*(3.1) are all eleven dimensional.
The characterization of isosymmetry (3.219) requires two isospaces and related isounits, one for the mutation of spacetime (st) with spacetime isounit Ist* and one for the mutation of the two-dimensional complex unitary spin space withspin isounit Ispin. From the positive-definiteness of these isounits, we assume the following diagonal realization (and leave very intriguing off-diagonal realizations to interested reader, see EHM-II)
CASE I: Dirac-Santilli isoequation without spin mutation
It is easy to prove that isogenerators (3.220) realized via isogammas (3.225) verify all isocommutators (3.77)-(3.79) and the interested reader is encouraged to verify.
Note that, in this case, no isotopy for the spin is needed because automatically provided by the assumed spacetime isotopy, resulting in a new realization of the regular Pauli-Santilli isomatrices, as the reader is suggested to verify. In any case, the spin isotopy can indeed be added, but has to preserve the spin 1/2 by assumption of the case considered, thus being inessential.
CASE II: Dirac-Santilli isoequation with spin mutation
In this case, we have the irregular realization of Eqs. (3.203), first identified by santilli in the above quoted paper of 1993-1995, today known as irregular Dirac-Santilli isoequation, that can be written:
From generators (3.201), the isotopic formulation of the spin of the isoelectron is given by
Note that the isocommutation rules of Π* are the same as those of P*(3.1), Eqs. (3.77)-(3.79), as the reader is encouraged to verify and that, despite the indicated differences,Π(3.1) is isomorphic to the conventional spinorial symmetry Π(3.1). in particular, the above isotopic SU(2)-spin remains isomorphic to SU(2), of course, at the abstract, realization-free level..
Additional mutations characterized by the Dirac-Santilli isoequation are those of the magnetic moment μ and electric dipole moment d, whose derivation has been worked out by Santilli in the above quoted 1993-1995 paper via a simple isotopy of the conventional derivation, resulting in the isolaws valid for the case of an axial symmetry along the third axis
It is an instructive exercise for the interested reader to verify that the above realization of the above irregular Dirac-Santilli isoequation cannot be constructed via a nonunitary transform of the conventional Dirac equation as for the regular case, but requires special maps.
3.11R. Direct universality and uniqueness of hadronic mechanics
The following properties are important for an understanding of the verifications and applications of hadronic mechanics:
1) Hadronic mechanics has been proved to be "directly universal," namely, admitting as particular cases all possible generalizations of quantum mechanics with brackets of the time evolution characterizing an algebra as defined in mathematics (universality), directly in the frame of the experimenter, thus avoiding any coordinate transformation (direct universality). This property is a consequence of the fact that Santilli's Lie-admissible algebras (Section 2.8) are the most general possible algebras admitting as particular cases all possible algebras as conventionally understood in mathematics.
2) All possible true generalizations of quantum mechanics, namely, those outside its classes of unitary equivalence but preserving an algebra in the brackets of the time evolution, are particular cases of hadronic mechanics.
3) Any modification of hadronic mechanics for the intent of claiming novelty, such as the formulation of basic laws via conventional mathematics, verifies the Theorems of Catastrophic Inconsistencies of Nonunitary Theories.
Note that the above direct universality applies not only for nonrelativistic but also for relativistic hadronic mechanics.
Yet another aspect studied in detail by Santilli for years is whether the structure of hadronic mechanics is unique or there exist inequivalent nonunitary generalizations of quantum mechanics that are equally invariant over time. The result of this study is that hadronic mechanics is indeed the sole mechanics verifying the conditions indicated (nonunitary time invariant structure).
As an example, in his original proposal to build hadronic mechanics, Santilli classified all possible modifications of the associative product AB of two matrices A, B via the use of a fixed matrix with the same dimension,
3.11S. EPR completion of quantum mechanics, hidden variables and all that
Santilli has repeatedly presented hadronic mechanics as a form of "completion" of quantum mechanics in honor of Einstein, Podolsky and Rosen who expressed historical doubts on the completeness of quantum theories. In fact, hadronic mechanics provides an explicit and concrete realization of hidden variables λ that are realized via the isotopic operator T according to the isoassociative eigenvalue equations
More generally, all branches of hadronic mechanics preserve the abstract axioms of quantum mechanics and merely provide broader realizations of the same axioms.
Santilli has also studied the nonunitary covering of Bell's inequalities and shown that, contrary to the quantum case, they do admit indeed a classical counterpart, thus altering the entire field of local realism.
Isorepresentation of the Lie-isotopic SU(2) algebra with
application to nuclear physics and local realism,
3.11T. Operator isogravity
As indicated in Chapter 1, one of the biggest scientific imbalances of the 20th century physics has been the absence of a consistent quantum formulation of gravity, since the quantization of the Riemannian representation is afflicted by a litany of inconsistencies. In particular, the noncanonical character of the classical formulation requires, for consistency, a nonunitary operator counterpart, thus activating the Theorems of Catastrophic Inconsistencies of Nonunitary Theories.
Santilli studied for decades the problem of a consistent operator form of gravity without any publication. He finally presented his solution at the 1994 M. Grossmann Meeting on Gravitation held at Stanford Linear Accelerator Center
Isotopic quantization of gravity and its universal isopoincare' symmetry
See also EHM Volumes I and II and the paper
Quantum isogravity
Santilli's argument is essentially the following. The impossibility of achieving a consistent operator form of gravity is due to curvature, since the latter requires a noncanonical classical structure with consequential nonunitary operator formulation and related catastrophic inconsistencies.
Hence, Santilli formulated his isogravitational theory indicated in Section 3.10H in which Riemannian line elements are identically reformulated in the Minkowski-Santilli isospace via the decomposition of the metric g(r) = Tgr(r)m, Eq. (3.100), where m is the Minkowski metric, and Tgr is the gravitational isotopic element. The formulation of the isometric m* = Tgr(r)m with respect to the isounit as the inverse of the gravitational isotopic element, I*gr = 1/Tgr, eliminates curvature, thus restoring unitary on the Hilbert-Santilli isospace over isofields with isounits I*gr.
This discovery was made possible by the unification of the Minkowskian and Riemannian geometries into the Minkowski-Santilli isogeometry presented in detail in EHM Volume I, as well as in the memoir
Isominkowskian geometry for the gravitational treatment of matter and its isodual for antimatter,
Following the above advances, the achievement of a consistent operator formulation of gravity was elementary. In fact, relativistic hadronic mechanics includes gravity without any modification of its structure via the mere interpretation of its isotopic element as being that of gravitational nature. Again, the procedure merely requires the factorization of the Minkowski metric m from any given Riemannian metric m*(r) = Tgr(r)m, such as for the Schwartzschild's metric, and the use of relativistic hadronic equations. As an illustration, the procedure yields the Dirac-Santilli isoequation (3.203), for which the anticommutation of the isogamma matrices yields precisely the Schwartzschild's metric, Eq. (3.204).
3.11U. Iso-grand-unification
There is no doubt that one of Santilli's biggest scientific contributions has been the achievement of the first axiomatically consistent grand unification of electroweak and gravitational interactions without pre-existing comparisons for consistency, mathematical beauty and physical content, to the Foundation's best knowledge (the indication of equally consistent grand unification is encouraged for comparative listing in this section). Here are summary comments released by Santilli:
The achievement of a consistent grand unification has been, by far, the most complex research problem I ever confronted due to the vastity and diversification of the required knowledge. Also, the more I worked at a solution, the bigger the problems with consequential widening of the field. Without any expectation that colleagues would agree, my conclusions following decades of work at the problem are the following:
1) Antimatter. I had to reject all preceding attempts at a grand unification, including that by Einstein, because of unsurmontable inconsistencies caused by antimatter. In fact, electroweak theories beautifully represent matter and antimatter, while a Riemannian gravitation does not, as nowadays well known. Only after achieving the isodual mathematics and related isodual theory of antimatter I was finally able to resolve these inconsistencies with a judicious decomposition of electroweak theories into advanced solutions and their isoduals with a corresponding gravitational and isodual counterpart allowing full democracy between matter and antimatter at all levels.
2) Curvature. After years of failed attempts along orthodox lines, I had to admit to myself that the representation of gravity via a curved spacetime renders any grand unification simply impossible. This was due to a litany of inconsistencies originating from attempting the combination of a theories structurally flat in spacetime, such as electroweak theories, and a gravitational theory that is structurally curved in spacetime. In particular, any reformulation of electroweak theories on a curved manifold to achieve geometric compatibility with gravitation, lead to unsurmontable catastrophes, such as the loss of physical meaning of electroweak theories at the operator level. These inconsistencies were determinant for my decision to cross the scientific "Rubicon" and abandon curvature for a covering theory of gravitation without curvature. That generated the birth of isogravitation.
3) Covariance. A third litany of inconsistencies originated from the fact that electroweak theories are beautifully structured by gauge and spacetime symmetries, while gravitation had none. The use of the customary "covariance" adopted by gravitational studies throughout the 20th century caused additional catastrophic inconsistencies, such as the lack of physical meaning of electroweak theories due to the general impossibility to predict the same numerical values under the same conditions at different times. The resolution of this third class of inconsistencies required the laborious construction of the Lie-isotopic theory that, in turn, permitted the construction of the Lorentz-Poincare'-Santilli universal isosymmetry of isogravitation.
The combination of all my studies, including the various new mathematics, the isodual theory of antimatter, the Lie-isotopic theory and relativistic hadronic mechanics, then finally lead to the iso-grand-unification with an axiomatically consistent inclusion of mutually compatible electroweak and gravitational theories for matter and antimatter.
The final solution I proposed is so elementary to be deceptive, because I essentially introduced gravitation where nobody looked for, in the unit of electroweak theories. However, by looking in retrospect, I can say that the virtual entirety of my research was ultimately aimed at the achievement of an axiomatically consistent grand unification. The diversification and novelty of the research illustrates the complexity of the problem of grand unification beyond the level of biased academic views.
In fact, following decades of research, Santilli finally released his iso-grand-unification at the VIII Marcel Grossmann Meeting on Gravitation held in Jerusalem, Israel, in 1996, as well as in related papers provided below,
Unification of gravitation and electroweak interactions
Isotopic grand unification with the inclusion of gravity
Isotopic unification of gravity and relativistic quantum mechanics and its universal isopoincare' symmetry
The most comprehensive and updated presentation of the iso-grand-unification is available in the five volumes of HMMC.
FOR THE CONSTRUCTION OF HADRONIC MECHANICS,
released in the preprint
Relativistic hadronic mechanics: nonunitary, axiom-preserving
completion of relativistic quantum mechanics
R. M. Santilli, IBR preprint TH-06-25 (1996)
For the final version, download the published version
Found. Phys. Vol. 27, 625-729 (1997)
,p>
and other Journals.
R. M. Santilli,
ICTP preprint # IC/91/258 (1991)
published in "Santilli's 1991 Papers at the ICTP", International Academic Press (1992)
verifies all ten conventional total conservation laws when the nonselfadjoint forces verify the following simple algebraic conditions
where ∗ and ∧ denote scalar and vector products, respectively.
R. M. Santilli,
ICTP [preprint # IC/91/259 (1991)
published in "Santilli's 1991 Papers at the ICTP", International Academic Press (1992)
in the isotime, isocoordinates and isovelocities
with real-valued, positive-definite isounits
Then, the Newton-Santilli isoequations can be written
namely, Newton's equations with nonpotential forces on conventional spaces over conventional numbers are turned into a form with sole potential forces on isospace over isonumbers, by embedding all nonpotential forces in the isounits, here expressed via isocoordinates and isoderivatives.
for which Eqs. (3.134) become for the simpler one-dimensional case with
nk = 1, k = 1, 2, 3, and the simplification m* x* = m Em Tm = m,
with simple solution for v constant
from which endless examples can be derived.
namely, the analytic equations with external terms on conventional spaces over conventional fields are identically rewritten in a form without external terms when formulated on isospaces over isofields.
whose brackets coincide with the conventional Poisson brackets at the abstract level.
for which
The first important consequence is that the Hamilton-Santilli isomechanics admits indeed an action principle. In fact, under the preceding simple realization Eqs. (3.139) can be derived from the isoaction principle
where one should note that the isoproduct for the space component is different than that for the time component.
For open irreversible single-valued or multi-valued or antimatter systems we have the Hamilton-Santilli geno-, hyper and isodual mechanics, respectively, we cannot review here. We can merely indicate that, in this case, at least one of the isounit must be given by a nonsymmetric matrix to assure the lack of invariance under time reversal.
thus setting the foundations for "quantized orbits" characterized by h/2π.
where one should note that I*r is the coordinate isounit. The preceding expression characterizes the lifting of Planck's constants into the space isounit
under the subsidiary condition (verified naturally by all isounits used in hadronic mechanics)
Expressions (3.150), (3151) constitute the conceptual foundations of hadronic mechanics. Recall that, by central assumption, quantum mechanics is valid for the exterior problem of point particles in vacuum, while hadronic mechanics is assumed valid for the interior problem of extended particles moving within a medium composed by other particles, as expected for the constituents of hadrons, nuclei and stars, of course, according to different degrees of mutual penetrations.
A. O. E. Animalu and R. M. Santilli, in "Hadronic Mechanics and Nonpotential
Interactions," M. Mijatovic, Editor, Nova Science, New York, pp. 19--26 (l990).
isonormalization
or
isoexpectation values for an operator Q
and related theory of isolinear operators on Η* over F* where from now on, unless otherwise indicated, I* and T refer to the space isounit and isotopic elements, respectively. .
Consequently, any physical quantity that is observable for quantum mechanics is equally observable for the covering hadronic mechanics.
with isoexpectation value
For details, extention to geno-, hyper- and isodual cases, and historical notes we refer the interested scholar to the 1995 EHM Volumes I and II.
where all coordinates and their derivatives are isotopic (even if not indicated due to limitations of the hmtl language).
where: one should note the natural emergence of the isodifferential calculus; as well as the last condition expressing the independence of the isowavefunction from the momenta, which condition is crucial for hadronic mechanics to be an axiom-preserving covering of quantum mechanics.
with infinitesimal form easily derivable from the preceding expression (where we ignore again for simplicity the isotopy of time)
and canonical isocommutation rules also reached for the first time in the 1996 RCMP memoir
For details, we suggest study EHM Volumes I and II and HMMC Volume III.
where, as one can see, there is no longer a singularity at r = ro under a suitable selection of the isotopic element. In turn, it is evident that
The isodelta function was presented for the first time in the paper
H. C. Myung and R. M. Santilli,
Hadronic Journal Vol. 5, pages 1277-1366 (1982).
M. Nishioka, Lettere Nuovo Cimento Vol. 39, pages 369-372 (1984).
M. Nishioka,
Hadronic J. Vol. 7, 1636-1679 (1984)
Figure 3.14. An illustration (left) of the origin of the divergencies of quantum mechanics in the singularity of Dirac's delta function δ(r - ro)at the value r = ro, and their removal ab initio in hadronic mechanics (right) by the Dirac-Myung-Santilli isodelta function that no longer admits the preceding divergencies for a suitable selection of the isotopic element, here considered as being dependent on (r-ro)2. In fact, the removal of the divergencies at the indicated level carries over at all levels the scattering and perturbation theories of hadronic mechanics.
A. O. E. Animalu and R. M. Santilli, for the Procveedings of the 2008 Yard Conference, submoitted for publication.
with interconnection crucial for consistent time reversal images
in which case the right and left genounits are indeed the correct units for both products.
that, as one can see, is indeed irreversible because it is inequivalent to its time reversal image. Similarly, we have: the Hamilton-Santilli genoequations to the right
related genoaction to the right and Hamilton-Jacobi-Santilli genoequations to the right here omitted for brevity; the Schroedinger-Santilli genoequations to the right
action on a geno-Hilbert space to the right, and the Heisenberg-Santilli genoequations evidently including both actions to the right and to the left because originating from corresponding universal enveloping genoassociative algebras (see Section 2.8)
with corresponding genotopies of all remaining aspects of the isotopic branch of hadronic mechanics.
with all multi-valued hyperstructures following from the above basic assumption on the fundamental unit.
to the totality of the quantities for matter and the totality of their operations.
In the corresponding case of two body hadronic systems, the constituents are at mutual distances equal or smaller than 1 fm = 10-13 cm, in which case the preceding point-like abstraction of the constituents is no longer valid because the actual extended character of the constituents, their actual shape, their density and other features, directly affect the dynamics.
x exp[ − F(t, r, p, E, μ, ψ ψ*, ...) ∫ ψ1†(r) ψ2(r) dr3],
namely, hadronic mechanics recovers quantum mechanics uniquely and identically for all mutual distances of particles bigger than their size.
Diag. (n112, n122, n132)
Diag. (n212, n222, n232) x
x exp [ F(t, r, p, E, μ, ψ ψ*, ...) ∫ ψ1† ψ2 dr3].
the lifting of numbers n into isonumbers
the lifting of conventional associative product nm between two numbers n and m into the isoproduct
U [ H | ψ ) ] U† = (U H U†) (U U†)-1 [ U | ψ ) U†) =
H* T | ψ* ) = H* x* | ψ* ) =
U [ E | ψ* ) ] U† = E' | ψ* ),
and the following identification of the forward and backward genounit
The entire forward and backward genotopic branch of hadronic mechanics can then be constructed by applying the above nonunitary transforms to the totality of the quantum formalism. A similar procedure holds for the construction of the forward and backward hyperstructural branches of hadronic mechanics..
But, as stressed before, hadronic mechanics must be elaborated with its own mathematics to prevent inconsistencies. Hence, nonunitary transforms must be reformulated in the following isounitary transformations
W* x*[ E |ψ*) ] x* (W*)† = E |ψ*)'
in which one should note the invariance of the numerical value of the isotopic operator and of the isoeigenvalue.
R. M. Santilli,
Found. Phys. Vol. 27, 1159- 1177 (1997)
Relativistic hadronic mechanics is, of course, the most important branch of the mew discipline for experimental verifications (chapter 6), theoretical predictions (Chapters 7. 8) and industrial applications (Chapters 4, 5, 9). It comprises the isotopic, genotopic and hyperstructural liftings of conventional relativistic quantum mechanics for matter in non-Hamiltonian reversible, irreversible and multi-valued conditions, respectively, and their isoduals for antimatter in corresponding conditions.
R. M. Santilli,
Found. Phys. Vol. 27, 625-729 (1997)
R. M. Santilli, Ukraine Academy of Sciences (1995)
R. M. Santilli, Hadronic J. Vol. 1, 574-901 (1978).
Nonrelativistic hadronic mechanics outlined in the preceding sections is characterized by the Galilei-Santilli isosymmetry not presented in these lines for brevity, but treated in detail in the monographs
R. M. Santilli,
Hadronic Press (1991)
R. M. Santilli,
Hadronic Press (1991)
with isostates |e*> of a Hilbert-Santilli isospace, the symbol "e" indicating the electron as the primary represented quantity, and the asterisk indicating mutation into the isoelectron.
or equivalently
where: the isometric (namely a matrix with isonumbers as elements) has been simplified to the form M* = m*I*, thus avoiding the isomultiplication in the left hend side becasue M* T p* ... = m*p* ...; m' is the isorenormalized mass, C = c/n4 is the localk speed of lightt; and the isoproduct in the r.h.d. has been removed because trivial.
where ∂*k are the isoderivatives, and γ*k are the Dirac-Santilli isomatrices with antiisocommutation rules
showing the appearance of the fundamental isometric directly in the structure of the isoequation. We assume the reader has acquired at least a minimal knowledge of preceding sections to understand that the Dirac-Santilli isoequation introduces, for the first time Riemannian, Finslerian and other gravitational effects directly in the dynamics of the electron under interior conditions.
To identify the structure of the Dirac-Santilli isoequation, we must first review the isotopies of SU(2)-spin with particular reference to the isotopies of its fundamental representation via Pauli's matrices, first studies by Santilli in various works, such as
R. M. Santilli,
JINR rapid Comm. Vol. 6. 24-38 (1993)
R. M. Santilli,
Acta Applicandae Mathematicae Vol. 50, 177-190 (1998)
This case is characterized by the so-called regular isounitary isorepresentations of the Lie-Santilli isosymmetry SU*(2). This case can be easily constructed via a nonunitary transformation of the conventional Pauli matrices.
where s1 and s2 are non-null numbers. Assume for Santilli isounit the nonunitary transform
Then, the regular Pauli-Santilli isomatrices are given by
and verify the following isocommutation relations and isoeigenvalues expressions
The preservation of the conventional eigenvalues for spin 1/2 is evident, a feature that Santilli proved to extend to all spins (see EHM-II).
by consequently voiding Bell's inequality of final character, since no longer valid under Santilli isotopies. For technical details, one should study the seminal paper
R. M. Santilli,
Acta Applicandae Mathematicae Vol. 50, 177-190 (1998)
This case is characterized by the irregular isorepresentations of the Lie-Santilli SU*(2). the latter cannot any longer be derived via a trivial nonunitary transform of the Lie case and constitute an intrinsic new feature of the Lie-Santilli isotheory without any correspondence with the conventional theory, although the latter always remains a particular case.
The mutation of spin is then evident, as desired by Santilli and as needed by his physical and industrial applications (see next chapters).
that ensures the Lie-Santilli character of the isoalgebra.
Dirac-Santilli isoequation
Recall that the conventional Dirac equation represents an electron under the "external" electromagnetic field of the proton as well known, since a consistent extension of Dirac's equation to the two-body system constituted by the H-atom has not been achieved to this day. In this case, all conventional intrinsic characteristics of particles are preserved and, therefore, there are no mutations. In this case, we have ordinary "particles" characterized by the Lorentz-Poincare' symmetry (3.75) with generators (3.76) and commutation rules (3.77)-(3.79).
R. M. Santilli,
Chinese J. System Engineering and Electronics Vol. 6, 177-199 (1995)
,p>
with generators
and the same commutation rules as in Eqs. (3.77)-(3.79).
As for the Pauli-Santilli isomatrices, we have the following two cases:
Let |e> be the eigenstates of the conventional Dirac equation on the conventional Hilbert space over the field of complex numbers for the representation of an electron, and consider the following nonunitary transforms Let
The isostate on the iso-Hilbert space over the isofield of complex numbers representing the isoelectron. in this case is then defined by
The simplest possible version of the regular Dirac-Santilli isoequation on iso-Minkowski space for the characterization of | the isoelectron is given by
where the γ*s are the regular Dirac-Santilli isomatrices and m*ij is the isometric of the Minkowski-Santilli isospace.
This is the most important case for the synthesis of the neutron from a proton and an electron inside a stars studied in Chapter 5, because the latter synthesis requires a mutation of spin.
In this case, , the orbital isosymmetry SO*(3) of the isoelectron is characterized by the generators and related isocommutation rules
with isoeigenvalues
Note that the above particular realization of the isogroup SO*(3) is also locally isomorphic to the conventional SO(3) group (because the n's are positive-definite).
with isoeigenvalues
illustrating the spin mutation desired by Santilli. Note that the eigenvalues of the spin, not only are no longer 1/2, but they are generally no longer constant to represent the electron when in the core of a collapsing star, or other extreme internal conditions, under which the preservation of the quantum value 1/2 is a pure unverified belief.
The above laws provide a quantitative geometric representation of the well known semiclassical property recalled earlier that the deformation of a charged and spinning sphere necessary implies an alteration of its magnetic and electric moments. In particular, we have a decrease (increase) of the magnetic moment when we have a prolate (oblate) deformation.
and concluded that the only acceptable isotopy is the form ATB, because the alternative forms TAB (ABT) violate the right (left) distributive and scalar laws, thus preventing the use of an algebra in the enveloping operator algebras with consequential catastrophic inconsistencies.
A reason for the uniqueness is that the only possible representation of contact non-Hamiltonian interactions verifying the condition of time invariance is that via Santilli isounit. Invariance then follows since the unit is the basic invariant of all theories. Nonequivalent generalizations of quantum mechanics must then use a representation of non-Hamiltonian effects other than that via the isounit, by activating the Theorems of Catastrophic Inconsistency of Nonunitary Theories.
The hidden character emerges from the fact that, at the abstract, realization-free level, there is no distinction between the conventional associative action of the Hamiltonian on a Hilbert state and its isoassociative covering. In fact, at the abstract level one can write the modular action in the abstract right-associative form "H |ψ*)" for both quantum and hadronic versions, thus illustrating the truly "hidden" character of said variables.
R. M. Santilli,.
Acta Applicandae Mathematicae Vol. 50, 177-190 (1998)
R. M. Santilli,
in the Proceedings of "The Seventh Marcel Grossmann Meeting", R. T. Jantzen, G. M. Keiser and R. Ruffini, Editors, World Scientific Publishers pages 500-505(1994).
R. M. Santilli,
Communication in Theor. Phys. Vol. 2, pages 1-14 (1995)
R. M. Santilli,
Intern. J. Modern Phys. D Vol. 7, 351-407 (1998)
R. M. Santilli,
in the proceedings of the "Eight Marcel Grossmann meeting", Israel 1997, T. Piran and R. Ruffini, Editors, World Scientific, pages 473-475 (1999)
R. M. Santilli,
Found. Phys. Letters Vol. 10. 307-327 (1997)
R. M. Santilli,
in "Gravity, Particles and Spacetime", P. Pronin and G. Sardanashgvily, Editors, World Scientific (1996)